| 1.
| При какой ставке сложных процентов за 9 лет сумма удваивается?
| Сложные проценты
|
| FV=2
PV=1
n=9
Найти i?
| FV=PV(1+i)n =>
2=1(1+i)9
(1+i)9=2
9lg(1+i)=lg2
lg2=0.3
9lg(1+i)=0.3
lg(1+i)=0.033
(1+i)=1.08
i=1.08-1=0.08(8%)
| простая
|
|
| Ответ: Сумма удваивается через 9 лет при 8%годовых.
|
| 2.
| В день рождения внука бабушка положила в банк 1000 у. е. под 3% годовых. Какой будет эта сумма к семнадцатилетию внука?
| Простые и сложные проценты
|
| PV =1000
i =0,03
n = 17
найти FV?
|  => FV =1000*(1+0,03*17) = 1510 у. е. => FV =1000*(1+0,03*17) = 1510 у. е.
| простые
|
|
|  => FV=1000*(1+0,03)17=1000*1,65=1650 у. е. => FV=1000*(1+0,03)17=1000*1,65=1650 у. е.
| сложные
|
|
| Ответ: К семнадцатилетию внука, сумма будет составлять 1510 у.е. (при простых процентах) и 1650 у. е. (при сложных)
|
|
| 3.
| Как найти инфляцию за квартал, если известна годовая инфляция?
|
|
|
|
|
|
|
| Ответ: чтобы найти инфляцию за квартал, необходимо годовую инфляцию разделить на 4, но при этом полученный результат будет являться средним значением инфляции за год.
|
| 4.
|
|
|
|
|
|
|
|
|
|
| 5.
| Счет «СБ100» в Сбербанке обещает 2,9% за 100 дней. Сколько это составит процентов годовых?
| Простые
|
| r=2,9%
t=100 дн.
R-?
| R=365/t*r=>365/100*2,9=10,59%
|
|
|
| Ответ: Это составит 10,59% годовых.
|
| 6.
| Докажите строго при одной и той же ставке i наращение сложных процентов идеет быстрее, чем простых процентов при длине периода наращения, более единичного и медленне, если период наращения менее еденичного, т.е. докажите неравенства (1+i)t>(1+ti), если t>1 и (1+ i)i< (1+ ti), если 0<t<1. Докажите, что при удержании процентов, наоборот, простые проценты уменьшают сумму медленне, чем сложные.
| Простые и сложные
|
 >(1+ti),если t>1 и >(1+ti),если t>1 и  <(1+it),если 0<t<1 <(1+it),если 0<t<1
| Если t>1, t=3,i=20%
 >(1+3*0,2)=>1,728>1,6
Т.е.наращение сложных процентов идет быстрее, чем простых процентов при длине периода наращения, более единичного.
Если 0<t<1, i=20%, t=0,5 >(1+3*0,2)=>1,728>1,6
Т.е.наращение сложных процентов идет быстрее, чем простых процентов при длине периода наращения, более единичного.
Если 0<t<1, i=20%, t=0,5
 < (1+i*t/365) < (1+i*t/365)
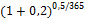 <(1+0,2*0,5/365)=>1,00025<1,00027
Наращение сложных процентов идет медленнее, если период наращения менее единичного.
При удержании процентов:
а) простые %: n=2, d=10%, P=1000
Pn=1000*(1-2*0,1)=800- сумма которая останется после удержания
б)Сложные проценты:
Pn=1000* <(1+0,2*0,5/365)=>1,00025<1,00027
Наращение сложных процентов идет медленнее, если период наращения менее единичного.
При удержании процентов:
а) простые %: n=2, d=10%, P=1000
Pn=1000*(1-2*0,1)=800- сумма которая останется после удержания
б)Сложные проценты:
Pn=1000*  =810 =810
|
|
|
| Ответ: Т.о., применив конкретные значения мы доказали, что при одной и той же ставке, наращение сложных процентов идет быстрее, чем простых процентов при длине периода наращения, более единичного и медленнее, если период наращения менее единичного.
При удержании процентов, наоборот, простые проценты уменьшают сумму медленнее, чем сложные.
|
| 7.
|
|
|
|
|
|
|
|
|
|
| 8.
| Докажите, что 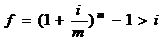 , т.е. эффективная ставка больше номинальной (m – натуральное число) , т.е. эффективная ставка больше номинальной (m – натуральное число)
|
|
|
| Представим, что под 20% годовых при ежеквартальном начислении процентов был взят кредит сроком на один год. По схеме сложных процентов ставка равна 20/4=5% => 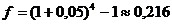 (по таблице М(4,5)=1,216). Ставка 21,6% - эффективная, а 20% - номинальная. Вторая меньше первой. (по таблице М(4,5)=1,216). Ставка 21,6% - эффективная, а 20% - номинальная. Вторая меньше первой.
|
|
|
| Ответ: доказано.
|
| 9.
|
|
|
|
|
|
|
|
|
|
| 10.
| Какую ставку должен назначить банк, чтобы при годовой инфляции 12%, реальная ставка оказалась 6%?
|
|
| j=6%
a=12%
Найти i
| Из уравнения Фишера:
(1+i)= (1+j)(1+ a), где i- номинальная ставка, j- реальная ставка, a - темп инфляции.
Получаем: i= (1+ j)(1+ a)-1= 18,72%.
|
|
|
| Ответ: банк должен назначить ставку 18,72%.
|
| 11.
| Наращение простых процентов с переменной ставкой. Пусть сложные проценты на k-й год равны 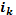 . Найдите наращенную сумму за n лет. . Найдите наращенную сумму за n лет.
| простые
|
Пусть
P -первоначальная сумма
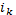 - простая процентная ставка в период k - простая процентная ставка в период k
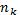 - продолжительность периода k
Найти S – наращенная сумма за n лет - продолжительность периода k
Найти S – наращенная сумма за n лет
| Тогда наращенная сумма определяется следующим способом
S =  ) )
|
|
|
| Ответ: S = 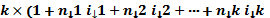 ) )
|
| 12.
|
|
|
|
|
|
|
|
|
|
|
| 13.
|
|
|
|
|
|
|
|
|
|
|
| 14.
| С помощью компьютера получены следующие значения
наращенных сумм через дробные промежутки времени. Проверьте компьютерные расчеты, используя формулы наращения простых и сложных процентов.
| Простые и сложные проценты
|
|
Дано:
Начальная сумма Процентная ставка 12%
Простые % 800 809,6 819,2 828,8
Сложные % 800 809,1 818,3 827,7
Доля единичного 0,0 0,1 0,2 0,3
промежутка начисле-
ния (t)
|
Решение:
Если 0 < t < 1, тогда
(1 + i)t < (1+ti)
t = 0,1, тогда
809,1 < 809,6 – расчет верен
t = 0,2, тогда
818,3 < 819,2 – расчет верен
t = 0,3, тогда
827,7 < 828,8 – расчет верен
|
|
|
| Ответ: все компьютерные расчеты верны.
|
| | | | | | | |
 => FV =1000*(1+0,03*17) = 1510 у. е.
=> FV =1000*(1+0,03*17) = 1510 у. е.
 => FV=1000*(1+0,03)17=1000*1,65=1650 у. е.
=> FV=1000*(1+0,03)17=1000*1,65=1650 у. е.
 >(1+ti),если t>1 и
>(1+ti),если t>1 и  <(1+it),если 0<t<1
<(1+it),если 0<t<1
 >(1+3*0,2)=>1,728>1,6
Т.е.наращение сложных процентов идет быстрее, чем простых процентов при длине периода наращения, более единичного.
Если 0<t<1, i=20%, t=0,5
>(1+3*0,2)=>1,728>1,6
Т.е.наращение сложных процентов идет быстрее, чем простых процентов при длине периода наращения, более единичного.
Если 0<t<1, i=20%, t=0,5
 < (1+i*t/365)
< (1+i*t/365)
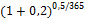 <(1+0,2*0,5/365)=>1,00025<1,00027
Наращение сложных процентов идет медленнее, если период наращения менее единичного.
При удержании процентов:
а) простые %: n=2, d=10%, P=1000
Pn=1000*(1-2*0,1)=800- сумма которая останется после удержания
б)Сложные проценты:
Pn=1000*
<(1+0,2*0,5/365)=>1,00025<1,00027
Наращение сложных процентов идет медленнее, если период наращения менее единичного.
При удержании процентов:
а) простые %: n=2, d=10%, P=1000
Pn=1000*(1-2*0,1)=800- сумма которая останется после удержания
б)Сложные проценты:
Pn=1000*  =810
=810
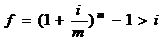 , т.е. эффективная ставка больше номинальной (m – натуральное число)
, т.е. эффективная ставка больше номинальной (m – натуральное число)
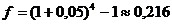 (по таблице М(4,5)=1,216). Ставка 21,6% - эффективная, а 20% - номинальная. Вторая меньше первой.
(по таблице М(4,5)=1,216). Ставка 21,6% - эффективная, а 20% - номинальная. Вторая меньше первой.
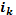 . Найдите наращенную сумму за n лет.
. Найдите наращенную сумму за n лет.
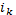 - простая процентная ставка в период k
- простая процентная ставка в период k
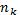 - продолжительность периода k
Найти S – наращенная сумма за n лет
- продолжительность периода k
Найти S – наращенная сумма за n лет
 )
)
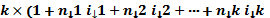 )
)