Линейная множественная регрессия

Контрольная работа

На тему: «Линейная множественная регрессия»

Студент Бухгамер С.А.

^{Подпись ФИО}

Группа НМТЗМ-102203

Екатеринбург 2021

Линейная множественная регрессия

При изучении множественной регрессии не существует графической интерпретации многофакторного пространства. При проведении экспериментов в такой ситуации исследователь записывает показания приборов о состоянии функции отклика y и всех факторов x_i, от которых она зависит. Результат исследований – это матрица наблюдений.

Здесь n – число опытов; k – число факторов; x_ij – значение j-го фактора в i-м опыте; y_i – значение выходного параметра для i-го опыта.

Задача линейной множественной регрессии состоит в построении гиперплоскости в (k+1)-мерном пространстве, отклонения результатов наблюдений y_i от которой были бы минимальными при использовании метода наименьших квадратов. Или, другими словами, следует определить значения коэффициентов b₀,..., b_j,..., b_k в линейном полиноме

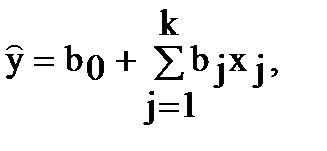
минимизирующее выражение

Процедура определения коэффициентов b₀,..., b_j,..., b_k не отличается от одномерного случая.

Для оценки тесноты связи между функцией отклика и несколькими факторами x₁, x₂,..., x_j,..., x_k используют коэффициент множественной корреляции R, который всегда положителен и изменяется в пределах от 0 до 1. Чем больше R, тем качественнее предсказания данной моделью опытных данных с точки зрения близости ее к функциональной. При функциональной линейной зависимости R=1.

Расчеты обычно начинают с вычисления парных коэффициентов корреляции, при этом вычисляются два типа парных коэффициентов корреляции:

1) – коэффициенты, определяющие тесноту связи между функцией отклика 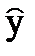и одним из факторов x_j;

2) – коэффициенты, показывающие тесноту связи между одним из факторов x_j и фактором x_u (j, u =1¸k).

Если один из коэффициентов окажется равным 1, то это означает, что факторы x_j и x_u функционально связаны между собой. Тогда целесообразно один из них исключить из рассмотрения, причем оставляют тот фактор, у которого коэффициент больше.

После вычисления всех парных коэффициентов корреляции можно построить матрицу коэффициентов корреляции следующего вида:

Парные коэффициенты корреляции не характеризуют тесноту связи, так как они вычисляются при случайно изменяющихся значениях других факторов.

Используя матрицу коэффициентов корреляции, можно вычислить частные коэффициенты корреляции, которые показывают степень влияния одного из факторов x_j на функцию отклика 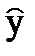при условии, что остальные факторы остаются на постоянном уровне.

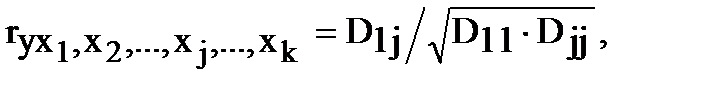
где D_1j – определитель матрицы, образованной из матрицы вычеркиванием 1-й строки и j-го столбца. Определители D₁₁ и D_jj вычисляют аналогично. Как и парные коэффициенты, частные коэффициенты корреляции изменяются от -1 до +1.

Значимость и доверительный интервал для коэффициентов частной корреляции определяются так же, как для коэффициентов парной корреляции, только число степеней свободы вычисляют по формуле

m = n -k*-2,

где k*=k-1 – порядок частного коэффициента парной корреляции.

Для вычисления коэффициента множественной корреляции 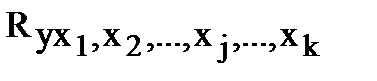используют матрицу коэффициентов корреляции:

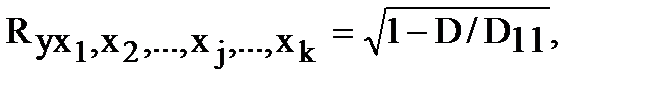
где D – определитель матрицы коэффициентов корреляции.

Множественный коэффициент корреляции дает оценку тесноты связи между у и совокупностью всех переменных x₁, x₂,..., x_j,..., x_k.

Если число опытов n сравнимо с числом коэффициентов l=k+1, связи оказываются преувеличенными. Поэтому следует исключить систематическую погрешность, физический смысл которой состоит в следующем. Если разность n и l будет уменьшаться, то коэффициент множественной корреляции R будет возрастать и при n-l=0 окажется равным R=+1, а уравнение регрессии превратится в функциональное уравнение гиперплоскости, которая пройдет через все n экспериментальных точек. Случайный характер переменных процесса при этом не может измениться. Поэтому требуется оценка значимости коэффициента множественной корреляции.

Значимость коэффициента множественной корреляции проверяется по критерию Стьюдента:

где – среднеквадратичная погрешность коэффициента множественной корреляции, рассчитываемая по выражению

Значимость R можно проверить также по критерию Фишера

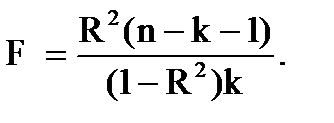
Если расчетное значение F превышает теоретическое F_a;m1;m2, то гипотезу о равенстве коэффициента множественной корреляции нулю отвергают и связь считают статистически значимой. Теоретическое (табличное) значение критерия Фишера определяется для выбранного уровня значимости a и числа степеней свободы m₁ = n-k-1 и m₂=k.

Если коэффициент множественной корреляции оказался неожиданно малым, хотя априорно известно, что между выходом y и входами x₁,...,x_k должна существовать достаточно тесная корреляционная связь, то возможными причинами такого явления могут быть следующие:

а) ряд существенных факторов не учтен, и следует включить в рассмотрение дополнительно эти существенные входные параметры;

б) линейное уравнение плохо аппроксимирует в действительности нелинейную зависимость , и следует определить коэффициенты уже нелинейного уравнения регрессии методами регрессионного анализа;

в) рабочий диапазон рассматриваемых факторов находится в районе экстремума функции отклика – в этом случае следует расширить диапазон изменения входных переменных, а также перейти к нелинейной математической модели объекта.