Обслуживание с ожиданием

Дисциплина:«Разработка САПР», МИС

 

 

Курсовой проект

 

 

Выполнен на кафедре:

«Технологии интегрированных автоматизированных систем»

 

Студент: Болтовский Виктор Алексеевич

 

 

Группа: 2ИВТ-4ДБ-256

 

 

Преподаватель, к.т.н: Цырков Георгий Александрович

 

 

Москва 2016 г.

Общие понятия СМО

Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропор­тах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и обо­рудования, на складах снабженческо-сбытовых организаций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Изучением таких ситуаций занимается теория массового обслуживания.

Теория систем массового обслуживания начала развиваться в начале 20 века. Основателем СМО считается математик Иохансен, сформулировавший в 1907 году предпосылки новой теории.

В 1909 году шведский математик Эрланг применил теорию вероятностей к исследованию зависимости обслуживания телефонных вызовов от числа поступающих на телефонную станцию вызовов. В СССР развитием данной проблематики занимался математик Хинчин, одной из главных работ которого, является «Теория очередей». Кстати этот термин теории СМО используется за границей.

СМО представляют собой системы специфического вида. Вообще СИСТЕМА – целостное множество взаимосвязанных элементов, неделимое на независимое подмножество.

Основа СМО - средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, операторы, би­летные кассиры, погрузочно-разгрузочные точки на базах и складах.

 

В теории систем массового обслуживания обслуживаемый объект называют требованием, а предназначением СМО как раз и является удовлетворение этих требований. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

В теории СМО рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. но­сит случайный характер. В силу этих причин одним из основных методов математического описания СМО является аппарат теории случайных про­цессов.

Предметом теории СМО является количественная сторона процессов, связанных с массовым обслуживанием.

Целью СМО является выработка рекомендаций по рациональному построению СМО и рациональной организации их работы и регулирования потока заявок.

Основной задачей теории СМО является изучение режима функциони­рования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслужи­вающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время без­действия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь оп­ределенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с просто­ем обслуживающих устройств.

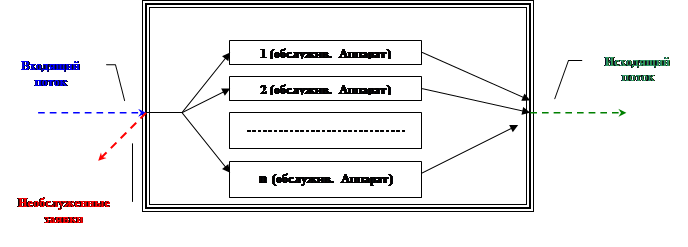
Структура СМО:

Классификация СМО и их

Основные элементы

СМО классифицируются на разные группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дис­циплины обслуживания требований.

По числу каналов n СМО бывают одноканальные (с одним обслуживающим уст­ройством) и многоканальными (с большим числом обслуживающих устройств). Многоканальные системы могут состоять из обслуживающих устройств как одинаковой, так и разной производительности.

По времени пребывания требований в очереди до начала обслуживания системы делятся на три группы:

1) с неограниченным временем ожидания (очередь). При занятости системы заявка поступает в очередь и в итоге будет выполнена (торговля, сфера бытового и медицинского обслуживания);

2) с отказами (нулевое ожидание или явные потери). «Отказанная» заявка вновь поступает в систему, чтобы её обслужили (вызов абонента через АТС);

3) смешанного типа (ограниченное ожидание). Есть ограничение на длину очереди (автосервис). Ограничение на время пребывания заявки в СМО (особые условия обслуживания в КБ).

В системах с определенной дисциплиной обслуживания поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в оче­редь.

Основными элементами СМО являются: входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований.

Эффективность функционирования СМО определяется её пропускной способностью – относительным числом обслуженных заявок.

Изучение СМО начинается с анализа входящего потока требований. Входящий поток требований представляет собой совокупность тре­бований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономер­ностей этого потока и дальнейшего улучшения качества обслуживания.

В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также ин­тервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными.

Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований и определяется следующим соотношением:

где Т - среднее значение интервала между поступлением очередных требований.

Для многих реальных процессов поток требований достаточно хоро­шо описывается законом распределения Пуассона. Такой поток называет­ся простейшим.

Простейший поток обладает такими важными свойствами:

1) Свойством стационарности, которое выражает неизменность вероятностного режима потока по времени. Это значит, что число требований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погрузку в среднем в сутки должно быть одинаковым для различных перио­дов времени, к примеру, в начале и в конце декады.

2) Отсутствия последействия, которое обуславливает взаимную не­зависимость поступления того или иного числа требований на обслужи­вание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от чис­ла требований, обслуженных в предыдущем промежутке времени. Напри­мер, число автомобилей, прибывших за материалами в десятый день ме­сяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.

 

3) Свойством ординарности, которое выражает практическую невозмож­ность одновременного поступления двух или более требований (вероят­ность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).

При простейшем потоке требований распределение требований, поступающих в систему подчиняются закону распределения Пуассона:

вероятность того, что в обслуживающую систему за время t поступит именно k требований:

где . - среднее число требований, поступивших на обслуживание в единицу времени.

Кроме того, наличие пуассоновского потока требований можно оп­ределить статистической обработкой данных о поступлении требований на обслуживание. Одним из признаков закона распределения Пуассона является равенство математического ожидания случайной величины и дисперсии этой же величины, т.е.

Одной из важнейших характеристик обслуживающих устройств, кото­рая определяет пропускную способность всей системы, является в ремя обслуживания.

Время обслуживания одного требования ()- случайная величина, которая может изменятся в большом диапазоне. Она зависит от стабиль­ности работы самих обслуживающих устройств, так и от различных пара­метров, поступающих в систему, требований (к примеру, различной гру­зоподъемности транспортных средств, поступающих под погрузку или вы­грузку).

Случайная величина полностью характеризуется законом распре­деления, который определяется на основе статистических испытаний.

При показательном законе распределения времени обслуживания ве­роятность события, что время обслуживания продлиться не более чем t, равна:

где v - интенсивность обслуживания одного требования одним об­служивающим устройством, которая определяется из соотношения:

, (1)

где - среднее время обслуживания одного требования одним об­служивающим устройством.

Важным параметром СМО является коэффициент загрузки , который определяется как отношение интенсивности поступления требований к интенсивности обслуживания v.

(2)

где a - коэффициент загрузки; - интенсивность поступления тре­бований в систему; v - интенсивность обслуживания одного требования одним обслуживающим устройством.

Из (1) и (2) получаем, что

Учитывая, что - интенсивность поступления требований в систему

в единицу времени, произведение показывает количество требова­ний, поступающих в систему обслуживания за среднее время обслужива­ния одного требования одним устройством.

Для СМО с ожиданием количество обслуживаемых устройств n должно быть строго больше коэффициента загрузки (требование установившегося или стационарного режима работы СМО):

.

В противном случае число поступающих требований будет больше суммар­ной производительности всех обслуживающих устройств, и очередь будет неограниченно расти.

Для СМО с отказами и смешанного типа это условие может быть ос­лаблено, для эффективной работы этих типов СМО достаточно потребо­вать, чтобы минимальное количество обслуживаемых устройств n было не меньше коэффициента загрузки :

Эффективность работы СМО характеризуется:

1)_группой показателей эффективности использования СМО:

- абсолютная пропускная способность – среднее число заявок, обслуживаемых в единицу времени (А);

- относительная пропускная способность – отношение АПС к среднему числу заявок, поступивших за единицу времени (Q);

- средняя продолжительность периода занятости СМО (Те);

- коэффициент использования СМО – средняя доля времени, в течении которого система занята обслуживанием заявок.

2)_Показателями качества обслуживания заявок:

- среднее время ожидания заявки в очереди (T line);

- среднее время пребывания заявки в СМО (T sys);

- вероятность отказа заявки в обслуживании без ожидания;

- вероятность немедленного приёма заявки;

- среднее число заявок в очереди (N line);

- среднее число заявок, находящихся в СМО (N sys).

Показатели эффективности функционирования пары «СМО – потребитель», (например, когда доход от СМО и затраты на её обслуживание измеряются в одних и тех же единицах, и отражает специфику работы СМО).

Обслуживание с ожиданием

СМО с ожиданием распространены наиболее широко. Их можно разбить на 2 большие группы - разомкнутые и замкнутые. Эти системы определяют так же, как системы с ограниченным входящим потоком.

К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на подналадку.

Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми (открытыми). Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным.

Мы рассмотрим здесь классическую задачу теории массового обслуживания в тех условиях, в каких она была рассмотрена и решена К.Эрлангом на n одинаковых приборов поступает простейший поток требований интенсивности . Если в момент поступления имеется хотя бы один свободный прибор, оно немедленно начинает обслуживаться. Если же все приборы заняты, то вновь прибывшее требование становится в очередь за всеми теми требованиями, которые поступили раньше и ещё не начали обслуживаться. Освободившийся прибор немедленно приступает к обслуживанию очередного требования, если только имеется очередь. Каждое требование обслуживается только одним прибором, и каждый прибор обслуживает в каждый момент времени не более одного требования. Длительность обслуживания представляет собой случайную величину с одним и тем же распределением вероятностей F(x). Предполагается, что при x 0.

где - постоянная.

Только что описанная задача представляет значительный прикладной интерес, и результаты, широко используются для практических целей. Реальных ситуаций, в которых возникают подобные вопросы, исключительно много. Эрланг решил эту задачу, имея в виду постановки вопросов, возникших к тому времени в телефонном деле.

 

Примеры

Пример 1.

Вызов абонента, имеющего только один телефонный номер, через АТС. Здесь поток заявок является случайным, если абонент занят, очередная поступающая заявка получает отказ в обслуживании; АТС – это одноканальная СМО (канал обслуживания – линия связи с телефонным номером абонента) с отказами.

Пример 2.

Работа пейджинговой компании. Многоканальная СМО, число каналов – количество дежурных операторов, СМО с ограниченной очередью (ограничение на длину очереди – память накопителя вызовов).

 

 

Пример 3.