Проверка гипотезы о виде закона распределения
Критерий Пирсона
(К.Пирсон (1857-1936) английский математик, статик, биолог, философ)
Одной из важнейших задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытному (эмпирическому) распределению, представляющему вариационный ряд.
Между теоретическим и эмпирическим распределениями неизбежны расхождения. При этом, возникает естественный вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений т. е. являются незначимыми, или они являются значимыми и связаны с тем, что теоретический закон распределения выбран неправильно. Ответ на этот вопрос дается применением критериев согласия.
В наиболее часто используемом на практике критерии согласия Пирсона 
в качестве меры расхождения 
рассматривается случайная величина , равная сумме квадратов отклонений относительных эмпирических частот (статистических вероятностей) 
, вычисленных по выборке объема 
от относительных теоретических частот 
, рассчитанных по предполагаемому распределению:
 (1)
|
где 
‑ число интервалов эмпирического распределения (вариационного ряда);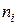 
‑ количество значений случайной величины 
, попавших в 
-ый интервал.
Числа 
называются соответственно эмпирическими и теоретическими частотами.
Р. Фишером была доказана следующая теорема.
Теорема. Если проверяемая гипотеза о виде распределения верна, то при большом объеме выборки критерий (1) имеет приблизительно -распределение с 
степенью свободы, где ‑ число интервалов эмпирического распределения,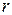 
‑ число оцениваемых параметров распределения.
В теореме указывается, что критерий (1) имеет -распределение только при больших объемах выборки . Поэтому в каждом частичном интервале вариационного ряда должно содержаться не менее 5-10 наблюдений (значений случайной величины ). В противном случае соседние интервалы следует объединить.
Схема применения критерия сводится к следующему:
1. Определяется мера расхождения эмпирических и теоретических час-
тот по формуле (1);
2. Для выбранного уровня значимости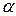 
по таблице -
распределения находится критическое значение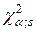 
при числе степеней свободы .
3. Если фактически наблюдаемое значение больше критического,
т. е. 
, то гипотеза 
отвергается, если 
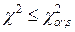, гипотеза не противоречит опытным данным.
Пример. Результаты исследований прочности на сжатие (случайная величина )
200 образцов бетона представлены в виде сгруппированного вариационного ряда.
Интервалы прочности, 
| Среднее значение интервала, 
| Частота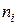
|
| 190-200 200-210 210-220 220-230 230-240 240-250 |
Требуется проверить нулевую гипотезу о нормальном законе распределения прочности на сжатие при уровне значимости 
.
Решение. Из условия следует, что точные параметры гипотетического нормального закона с функцией распределения (41)
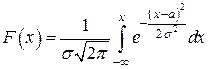
неизвестны, поэтому гипотезу можно сформулировать следующим образом: прочность на сжатие является функцией нормального распределения с параметрами
.
Для проверки гипотезы вычислим точечные оценки математического ожидания и среднего квадратического отклонения нормально распределенной случайной величины:
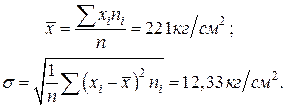
Вычислим теоретические вероятности попадания значений случайной величины в частичные интервалы 
по теореме 11.7 для нормального распределения
,
где
Дальнейшие вычисления, необходимые для определения расчетного значения 
приведены в расчетной таблице.
По таблице ‑ распределения (приложение 3) при заданном уровне значимости и числе степеней свободы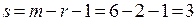 
, критическое знание
.
Расчетная таблица
| Интервалы изменения случайной величины
| Часто-ты
| Нормирован-ные интервалы 
| Теоретические
вероятности
| 
| 
| |
| 190-200 | 
| 0,045 | 0,11 | |||
| 200-210 | 
| 0,142 | 28,4 | 5,76 | 0,20 | |
| 210-220 | 
| 0,281 | 56,2 | 0,04 | 0,00 | |
| 220-230 | 
| 0,299 | 59,8 | 17,61 | 0,29 | |
| 230-240 | 
| 0,171 | 34,2 | 17,64 | 0,52 | |
| 240-250 | 
| 0,062 | 12,4 | 2,56 | 0,23 | |
| 1,000 | 200,0 | 
|
Так как 
, то нет оснований для отклонения нулевой гипотезы о нормальном законе распределения прочности бетона на сжатие с параметрами 
В некоторых случаях уровень значимости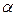 
предварительно не задается, а по имеющейся выборке рассчитывается значение критерия. Затем определяется тот максимальный уровень значимости, при котором критерий еще попадает в область принятия гипотезы. Этот максимальный уровень значимости, при котором гипотеза принимается, называется критическим уровнем значимости. Если критический уровень ниже заданного уровня значимости 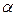, то гипотеза отклоняется.
Вывод: Анализ результатов показывает, что критерий Пирсона имеет наименьшее значение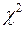 
= 0,63441 и ему соответствует самое большое значение критического уровня значимости p =0,42574 в случае проверки гипотезы о нормальном распределении случайной величины. Таким образом, в окончательном варианте следует принять гипотезу о том, что исследуемая случайная величина подчинена нормальному закону распределения.