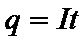(7)
и работа, совершаемая током
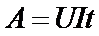(8)
Для оценки энергетических условий важно знать, сколь быстро совершается работа, т. е. определить мощность
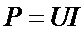(9)
Для резистивных элементов выражение (9) можно преобразовать, воспользовавшись законом Ома
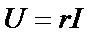
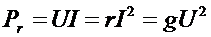(10)
Для источника ЭДС, направление которого совпадает с направлением тока (рис.6, а), мощность сторонних сил
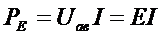(11)
 |
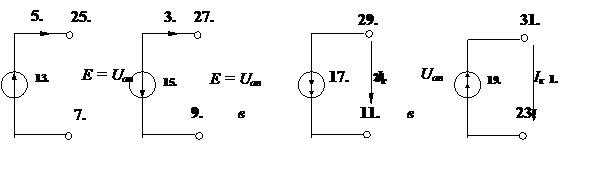а) б) в) г)
Рис.6. Примеры возможных соотношений между ЭДС и током (а, б) и током и напряжением (в и г) на зажимах источников
Если направления ЭДС и тока противоположны (рис.6, б), то мощность источника
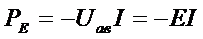(12)
(например, при зарядке аккумулятора). Аналогично мощность источника тока
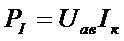, (13)
если направления тока внутри источника и напряжения между его выводами противоположны (рис. 6, г). В противном случае мощность источника
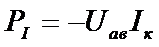(14)
(рис.6, в), т. е. источник получает энергию из внешней цепи.
Заметим, что идеальные источники ЭДС и тока могут развивать бесконечно большую мощность. Действительно, подключим к каждому источнику приемник с сопротивлением нагрузки R. В первом случае, если 
, ток 
и, следовательно, мощность
,
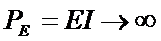а во втором случае, если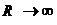 
, напряжение 
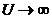и мощность
.
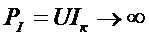В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников энергии (в частности, источников тока и источников ЭДС) равна арифметической сумме мощностей всех приемников энергии (в частности, резистивных элементов):
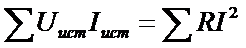(15)
или
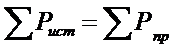(16)
Законы, используемые для расчета электрических цепей
Закон Ома
- для пассивного участка цепи:
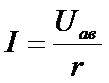, (17)
где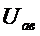 
- напряжение между точками a и в;
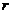- сопротивление участка цепи (рис.7.)
|
|
 |
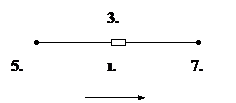Рис.7. Пассивный участок цепи
-для активного участка цепи:
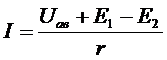, (18)
где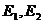 
- ЭДС источников (рис.8.)
 |
Рис.8. Активный участок цепи
Законы Кирхгофа
- первый закон Кирхгофа:
 |
алгебраическая сумма токов в узле электрической цепи равна нулю.При этом токи, направленные к узлу, берутся с одним, а направленные от узла - с другим знаком (рис. 9):
 |
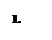Рис.9. К первому закону Кирхгофа
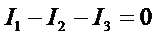
-второй закон Кирхгофа:
алгебраическая сумма падений напряжений на сопротивлениях участков контура равна алгебраической сумме ЭДС, входящих в этот контур. При этом падения напряжения и ЭДС, совпадающие с обходом контура входят в сумму со знаком плюс, а не совпадающие - со знаком минус (рис.10.):
 |
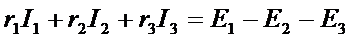
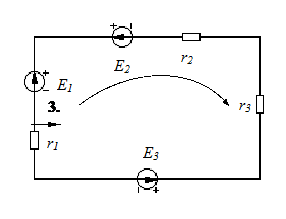Рис.10. Ко второму закону Кирхгофа
Эквивалентное преобразование резистивных цепей
Пассивные электрические цепи с последовательным, параллельным и смешанным соединением элементов относятся к простым цепям, если в них используется один источник ЭДС. Расчёт таких цепей чаще всего сводится к расчёту токов в ветвях и напряжений на отдельных участках эквивалентных схем.
Метод преобразования состоит в том, что заданная сколь угодно сложная электрическая цепь преобразуется в простейшую, ей эквивалентную, которая рассчитывается (чаще всего) по закону Ома, а затем, если требуется, вновь возвращаются к исходной схеме и находят токи в ней. Рассмотрим эквивалентное преобразование цепей с различными видами соединения элементов.