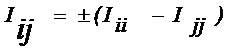В сложных цепях элементы могут быть соединены между собой самым различным способом. В некоторых случаях элементы могут образовывать особые группы, в которых нет ни последовательного, ни параллельного соединения элементов. Наиболее часто встречаются группы из трех элементов, соединенных звездой или треугольником. Для упрощения расчета таких схем удобно заменить звезду эквивалентным треугольником или же треугольник эквивалентной звездой сопротивлений. Эквивалентность преобразования заключается в том, что после преобразования токи и напряжения в остальной части цепи, не затронутой преобразованием, не изменяются; не изменяются и потенциалы точек а, в и с.
 |
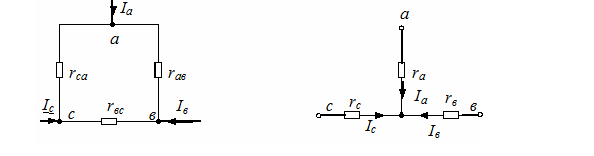a) б)
Рис. 14. Соединение элементов треугольником (а)и звездой (б).
Для выполнения условий эквивалентности необходимо, чтобы сопротивления между любой парой точек при соединении треугольником и соединении звездой были одинаковы.
Вычислим сопротивления между точками а и в, в и с, с и а в треугольнике и в звезде и приравняем их из условия эквивалентности преобразования:
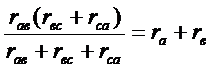
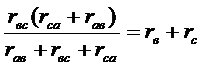(35)
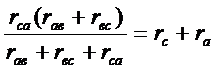
Решая систему относительно сопротивлений звезды (сопротивления треугольника заданы), получим формулы для преобразования
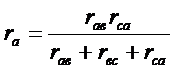
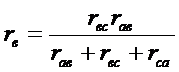(36)
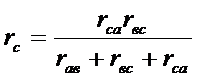
Решая же систему относительно сопротивлений треугольника (сопротивления звезды заданы), получим формулы для преобразования
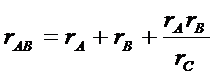
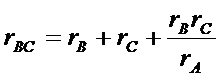(37)
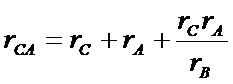
Для расчёта разветвлённых цепей с несколькими источниками энергии (сложных цепей) рекомендуется несколько методов:
1) Метод уравнений Кирхгофа;
2) Метод контурных токов;
3) Метод узловых потенциалов;
4) Метод наложения (суперпозиции);
5) Метод эквивалентного генератора;
|
|
Целесообразность выбора метода расчёта величин токов зависит от конфигурации схемы.
При расчёте разветвлённых цепей используют понятия элементов конфигурации цепи: ветвь, узел, контур.
Методы расчета сложных электрических цепей
Метод непосредственного применения законов Кирхгофа
1.Определяется число узлов схемы n и число ветвей в схеме m.
2.Произвольно выбирается направление токов во всех ветвях и направление обхода (m-n+1) контуров.
3.Составляется система из т уравнений, где (n-1) уравнений составляются по I закону Кирхгофа, и (m-n+1) уравнений - по II закону Кирхгофа.
4. Решается система из т линейных уравнений, из которой определяются токи в ветвях.
Для расчета цепи по заданным сопротивлениям и ЭДС нумеруют узлы и задают условно положительные направления токов в ветвях. В схеме на рис. 15. число ветвей m = 6, число узлов n = 4. Число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (n – 1) = 3, по второму закону (m – n + 1) = 3. Получаем систему из шести уравнений:
 |
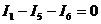
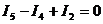
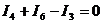
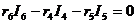
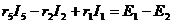
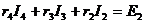
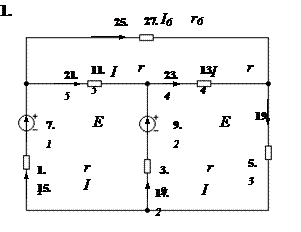Рис.15. К расчету цепи по законам Кирхгофа
Метод контурных токов
В основе метода лежит 2-й закон Кирхгофа и два предположения: в каждом контуре протекают независимые друг от друга расчётные токи, называемые контурными, а ток каждой ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь.
При этих предположениях оказывается, что для расчёта токов в схеме, достаточно ограничиться составлением только контурных уравнений по 2-му закону Кирхгофа.
|
|
Это позволяет сократить число уравнений системы до (m-n+1).
1.Определяется число узловсхемы n и число ветвей в схеме m.
2.Произвольно выбирается направление токов во всех ветвях и одинаковое (по часовой стрелке или против часовой стрелки) направление обхода (m-n+1) контуров.
3.Задаются контурные токи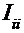 
как собственные токи каждого независимого контура схемы. Их направление совпадает с выбранным направлением обхода контура.
4.Вычисляются:
- контурные э.д.с.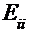 
как алгебраическая сумма входящих в контур э.д.с. источников;
- собственные сопротивления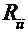 
контуров как сумма всех входящих в контур сопротивлений;
- общие сопротивления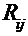 
контуров как сумма сопротивлений двух смежных контуров.
5.Составляется система из (m-n+1) уравнений по II закону Кирхгофа, в которых справа – контурные э.д.с., а слева – сумма падений напряжения, созданного контурным током своего контура на собственном сопротивлении контуров (со знаком «+») и созданных контурными токами смежных контуров на общих сопротивлениях контуров (со знаком «-»).
6.Решается система (m-n+1) линейных уравнений, из которых определяются контурные токи.
7.Определяются токи в ветвях через контурные токи. В ветвях, общих для смежных контуров, токи равны алгебраической сумме соответствующих контурных токов:
