Позволяет сократить число уравнений до (n-1).
1.Определяется число узлов схемы n.
2.Произвольно выбирается направление токов во всех ветвях.
3.Выбирается базовый узел, потенциал которого принимается равным нулю. (Целесообразно выбрать базовым узел, к которому примыкает максимальное число ветвей).
4.Определяются:
- собственные проводимости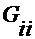 
(n-1) узлов как сумма проводимостей всех примыкающих к узлу ветвей;
- общие проводимости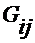 
между двумя узлами 
и j как сумма проводимостей между ними;
- узловые токи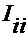 
как алгебраическая сумма 
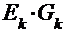, где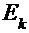 
- э.д.с. к- ой ветви, примыкающей к к- ому узлу (
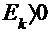, если направлена к 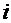- тому узлу), 
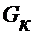- проводимость к- ой ветви.
5.Составляется система из (n-1) уравнений по I закону Кирхгофа, в которых справа – узловые токи, а слева – сумма потенциала собственного узла, умноженного на собственную проводимость узла (со знаком «+») и потенциалов смежных узлов, умноженных на общую проводимость между узлами (со знаком «-»).
6.Решается система (n-1) уравнений, из которой определяются потенциалы узлов по формулам.
8.Определяются токи в ветвях через потенциалы узлов:
,
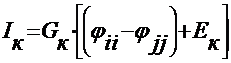где 
, если к- тый ток течет от узла 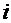к узлу j;
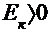, если совпадает по направлению с к- тым током.
Метод узлового напряжения (двух узлов)
Является частным случаем предыдущего метода и применяется для расчета токов в ветвях с двумя узлами, между которыми включены активные и пассивные ветви. Идея метода состоит в том, что по расчётной формуле определяется напряжение между двумя узлами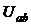 
, называемое узловым, а затем по закону Ома рассчитываются токи в ветвях.
1. Выбирается направление тока в ветвях, одинаковое для всех ветвей (например, от узла b к a).
2. Определяется узловое напряжение:
,
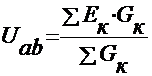где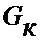 
- проводимость к-той ветви;
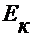- э.д.с. к-той ветви (
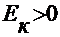, если направлена по току в к-той ветви)
3. Определяются токи в ветвях:
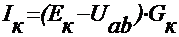
Метод наложения токов
Принцип наложения является выражением одного из основных свойств линейных систем любой физической природы и применительно к линейным электрическим цепям формулируется следующим образом: ток в какой-либо ветви сложной электрической цепи равен алгебраической сумме частичных токов, вызванных каждым действующим в цепи источником электроэнергии в отдельности.
Позволяет свести расчет разветвленной электрической цепи с несколькими источниками питания к нескольким расчетам этой же цепи с одним источником питания.
1. Составляются частные схемы, в каждой из которых оставляют один источник э.д.с., замыкая все остальные накоротко.
2. Выбираются направления токов в ветвях частной схемы в зависимости от направления действующего в ней источника э.д.с.
3. Рассчитывают токи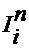 
в ветвях частной схемы, применяя метод «свертывания цепи», т.е. ее постепенного упрощения путем замены сложного соединения резисторов эквивалентными сопротивлениями и сведения схемы к одному эквивалентному сопротивлению. При расчете токов в ветвях схему «разворачивают» в обратном порядке.
4. Определяются токи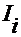 
в ветвях исходной схемы как алгебраическая сумма токов в ветвях частной схемы, причем 
, если совпадает с направлением в исходной схеме, и наоборот.
ЗАДАНИЕ ДЛЯ ВЫПОЛНЕНИЯ
Рис. 16. Схема цепи для расчета
1. Рассчитать эквивалентное сопротивление цепи (рис.16) относительно указанных согласно Вашему варианту зажимов, считая приемники во всех ветвях резистивными, а все источники ЭДС замкнутыми накоротко. Значение сопротивлений задано в таблице. Представить подробные расчеты и эквивалентную схему после каждого этапа преобразования.
2. Рассчитать токи в ветвях, применив метод свёртывания цепи, при условии действия в ней одного, указанного в таблице источника постоянной ЭДС, и разомкнув указанную в таблице ветвь. Привести подробные расчеты и эквивалентную схему после каждого этапа преобразования.
3. Определить токи в ветвях цепи методом составления уравнений по законам Кирхгофа и методом, указанным в таблице для вашего варианта.
Составить баланс мощностей для цепи.
| № варианта | Зажимы (задача 1) | ЭДС (задача 2) | Rнечетные Ом | Rчетные Ом | Eнечетные В | Eчетные В | Разомкнута ветвь с резистором (задача 3) |
| AB | Е1 | R1 | |||||
| ВС | Е2 | R2 | |||||
| CD | Е3 | R3 | |||||
| CG | Е4 | R4 | |||||
| EG | E5 | R5 | |||||
| AC | E6 | R6 | |||||
| EK | Е1 | R7 | |||||
| BD | Е2 | R8 | |||||
| FG | Е3 | R9 | |||||
| BL | Е4 | R10 | |||||
| AЕ | E5 | R11 | |||||
| BM | E6 | R12 | |||||
| DM | Е1 | R13 | |||||
| AG | Е2 | R1 | |||||
| BE | Е3 | R2 | |||||
| DE | Е4 | R3 | |||||
| DK | E5 | R4 | |||||
| DL | E6 | R5 | |||||
| AD | Е1 | R6 | |||||
| EF | Е2 | R7 | |||||
| AF | Е3 | R8 | |||||
| DG | Е4 | R9 | |||||
| AK | E5 | R10 | |||||
| ВF | E6 | R11 | |||||
| CF | Е1 | R12 | |||||
| CK | Е2 | R13 | |||||
| CL | Е3 | R1 | |||||
| AM | Е4 | R2 | |||||
| DF | E5 | R3 | |||||
| BG | E6 | R4 | |||||
| CM | Е1 | R5 | |||||
| BK | Е2 | R6 | |||||
| AL | Е3 | R7 |
ПРИМЕРЫРАСЧЕТА
Задача 5.1
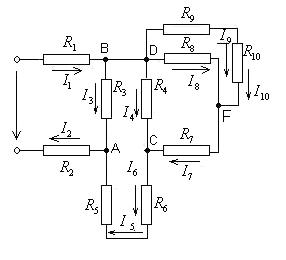
Рис. П1
Найти токи в ветвях схемы (рис.П1), если напряжение на входе U =23В, а сопротивления участков схемы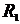 
= 
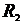=0,5 Ом; 
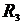=8 Ом, 
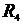=12 Ом, 
= 
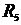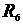=1 Ом; 
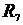=2 Ом; 
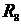=15 Ом; 
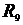=10 Ом, 
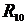=20 Ом.
Решение:
Эквивалентное сопротивление всей схемы находим путём постепенного упрощения (свёртывания) схемы. Для этого заменяем сопротивления отдельных участков, начиная с наиболее удалённых от входа, их эквивалентными сопротивлениями:
= 
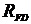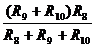=10 Ом; + 
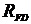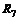=12 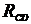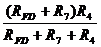Ом; 
= 
=6 Ом
+ 
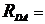
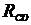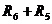=8 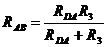Ом; 
=4 Ом
= 
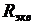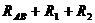=5 Ом.
Ток в неразветвлённой цепи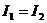 
определяется из соотношения = 
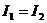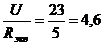А.
Падение напряжения между узловыми точками А и 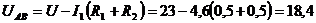В
В
Ток через резистор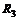 
определяем по формуле 
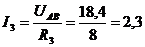А
Применяя 1-й закон Кирхгофа для узла А, находим токи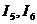 
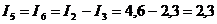А.
Определяем напряжение между узлами С и D.
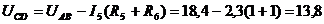В
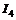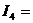
Определяем величину ток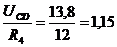а 
.
А
По первому закону Кирхгофа определяем ток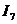 
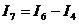=2,3-1,15=1,15 А
Падение напряжения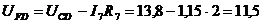 
В.
Определяем величину тока I 8
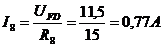
Определяем величину тока I 9= I 10
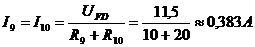или 
I9=I10=I7-I8=1,15-0,77=0,38A
Ответ: I1=I2=4,6A; I3=2,3A; I5=I6=2,3A; I7=1,15A; I8=0,77A; I9=I10=0,38A
Задача 5.2
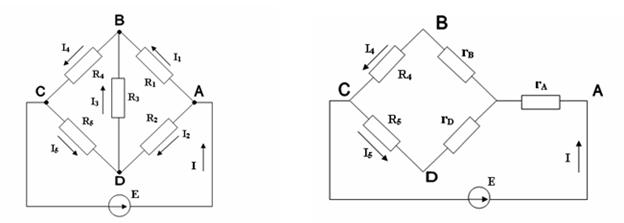
Рис.П2. Мостовая схема
Рис.П3. Преобразованная мостовая схема
Определить токи в ветвях мостовой схемы (рис.П2), если известны величины Е =4,4В; R1 =20 Ом; R2 =60 Ом; R3 =120 Ом; R4 =8 Ом; R5 =44 Ом
Решение:
Заменив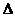 
ABD, образованный сопротивлениями R1, R2, R3, эквивалентной звездой, сопротивление лучей которой rA , rB, rD, получим простую схему смешанного соединения сопротивлений (Рис.П3.). Находим сопротивление лучей звезды
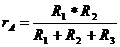=6 Ом; 
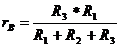=12 Ом; 
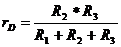=36 Ом
Заменив ABD, образованный сопротивлениями R1, R2, R3, эквивалентной звездой, сопротивление лучей которой rA , rB, rD, получим простую схему смешанного соединения сопротивлений (Рис.П3.). Находим сопротивление лучей звезды
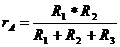=6 Ом; 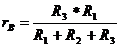=12 Ом; 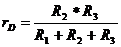=36 Ом
Определяем Rэкв цепи, состоящей из неразветвлённого участка rA и двух параллельных ветвей (R4 + rB) и (R5 + rD)
Rэкв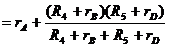 
= 22 Ом
Ток в неразветвлённой части схемы (Рис.П3)
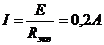
Ток в ветви с сопротивлениями R4, rB
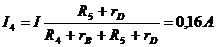
Ток в ветви с сопротивлениями R5, rD
Для определения токов I1, I2 , I3, которых нет в преобразованной схеме, найдём потенциалы узловых точек D и B.
Напряжение на сопротивлении R4
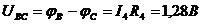
Напряжение на сопротивлении R5
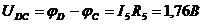
Полагая потенциал точки С равным нулю, получаем:
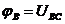и 
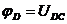
Напряжение на диагонали моста DB
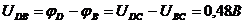
Переходя к схеме (рис.4), найдём токи ветвей
; 
; 
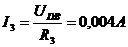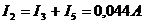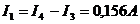
Ответ: I1=0,156А; I2=0,044A; I3=0,004A; I4=0,16A; I5=0,04A
Задача 5.3
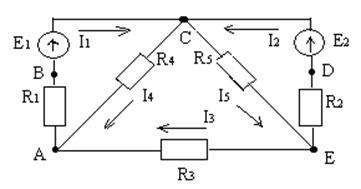
Рис.П.4
Определить токи во всех ветвях цепи методом уравнений Кирхгофа, если дано: E1=12B; E2=11B; R1=R2=1 Ом; R3=2 Ом; R4=9 Ом; R5=4 Ом.
Правильность выполненного расчёта проверить, составив баланс мощностей.
Решение.
Зададим произвольно направление токов во всех ветвях цепи и будем считать эти направления положительными. Они указаны стрелками на рис. П4. Токи будут алгебраическими величинами т. е. могут принимать положительные и отрицательные значения. Если после решения уравнений будет получено отрицательное значение для какого-либо из токов, то этот ток в действительности будет протекать в направлении
, противоположном выбранному и показанному на схеме (рис.П4). Схема имеет три узла А, С и Е, поэтому нужно составить два узловых уравнения по 1-му закону Кирхгофа, например:
для узла А I4=I1-I3.........(1)
и для узла E I5=I2+I3 …....(2)
Так как число неизвестных токов равно пяти, то нужно иметь пять уравнений, следовательно, три недостающих уравнения – контурные, которые составляются по 2-му закону Кирхгофа
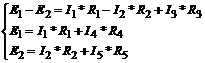или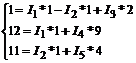 
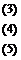
Применяя метод замены, освободимся от токов I4 и I5, заменив их в уравнениях (4) и (5) значениями из уравнений (1) и (2), соответственно.
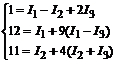
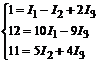
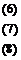
Из уравнения (8) находим
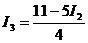(9)
и подставляем значение I3 в уравнение (3).
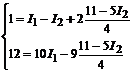
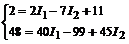
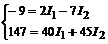
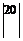
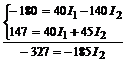
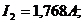
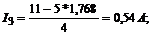
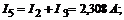
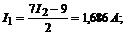
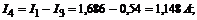
Баланс мощностей:
E1*I1+E2*I2=I1²*R1+I2²*R2+I3²*R3+I4²*R4+I5²*R5
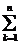Ek* Ik = 
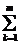I ² k*Rk, где
n- число источников питания (генераторов);
m- число сопротивлений в цепи (потребителей).
Проверка: 12*1,686+11*1,768=1,686 ² *1+1,768 ² *1+0,54 ² *2+1,148 ² *9+2,308 ² *4
20,237+19,448=2,842+3,125+0,583+11,861+21,307
39,685Вт = 39,718Вт
Ответ: I1=1,686A; I2=1,768A; I3=0,54A; I4=1,148A; I5=2,308A
Задача 5.4
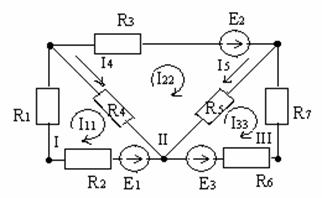
Рис. П5
В приведенной схеме найти токи в ветвях методом контурных токов, если E1=E2=10B; E3=8B; R1=R4=5 Oм; R2=4 Ом; R3=10 Ом; R5=R7=2 Ом; R6=1 Ом.
Решение.
Правило составления системы уравнений.
Система уравнений для 3-х контуров имеет вид:
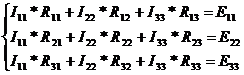
Рекомендуется, для однообразия в знаках сопротивлений, с разными индексами, все контурные токи направлять в одну и ту же сторону, например, все по часовой стрелке.
Если в результате решения системы уравнений какой-либо ток окажется отрицательным, то это будет означать, что в действительности, направление контурного тока обратно принятому за положительное.
В ветвях, не являющихся смежными между соседними контурами (например, в ветвях с сопротивлениями R1, R3 схемы), найденный контурный ток будет являться истинным. В смежных ветвях надо через контурные токи найти истинные. Например, в ветвях с R5 истинный ток равен разности I22–I33.
Находим значения протекающих токов через соответствующие сопротивления, с учётом рассмотренных выше рекомендаций.
; 
; 
; 
; 
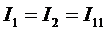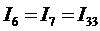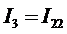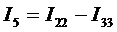
Решение:
В схеме три контура, обозначенных римскими цифрами. Выбираем направление всех контурных токов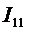 
, 
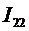и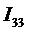 
по часовой стрелке.
Определяем:
;
;
.
; 
; 
.
; 
; 
.
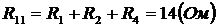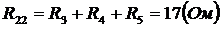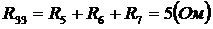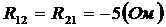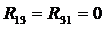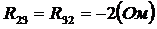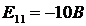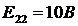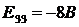Записываем систему уравнений:
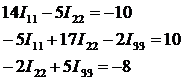
Решая систему, определяем токи в ветвях.
Ответ: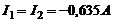 
; 
; 
; 
; 
.
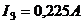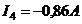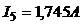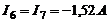Задача 5.5
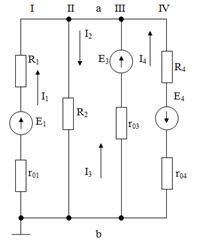
Рис. П6
Определить токи в ветвях схемы.
E1=110В; Е3=111В; Е4=108 В
r01=0,5 Ом; r03=1Ом; r04=0,2Ом -
внутренние сопротивления источников
R1=4,5Ом; R3=20Ом; R4=25,8Ом -
сопротивление нагрузок в ветвях.
Решение:
Схема имеет два узла a и b, между которыми включены четыре ветви, обозначенные римскими цифрами. Вторая ветвь не имеет источника ЭДС. Рассчитываем проводимости ветвей.
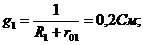
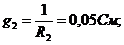
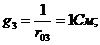
Узловое напряжение 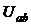(положительное направление от узла a к узлу b) равно:
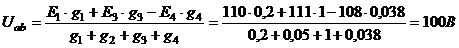
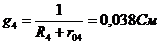
Токи в ветвях:
; 
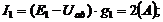
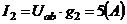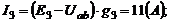
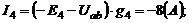
Ответ: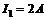 
; 
; 
; 
.
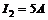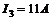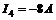Задача 5.6
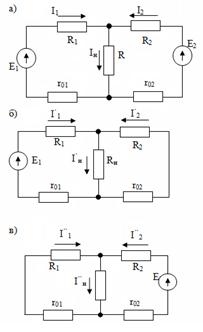
Рис.П7
В схеме (рис П7, а) определить токи в ветвях методом наложения.
Е1=13В, Е2=12,5В,
R1=R2=0,4 Ом,
Rн=2 Ом, r01=r02=0,1 Ом – внутренние сопротивления генераторов
Определить токи в ветвях I1, I2 и Iн в ветвях схемы.
Решение
Расчёт токов в ветвях сводится к расчёту частичных токов в более простых цепях (рис. П7 б и в). Затем найденные токи суммируются с учётом знаков.
В первой частичной схеме (б) действует только ЭДС Е1, а во второй (в) – только ЭДС Е2 (внешние и внутренние сопротивления остаются без изменений).
Ток неразветвленной части цепи (Rн), в двух параллельных ветвях разделится на токи, величины которых обратно пропорциональны сопротивлениям этих ветвей:
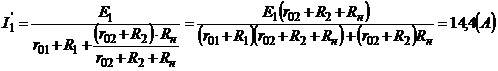
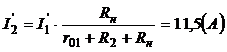
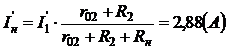
Аналогично определяются токи для второй частичной схемы
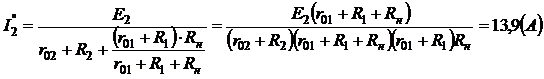
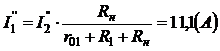
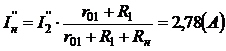
Если составляющие токов I`1, I`2, I`н и I``1, I``2, I``н наложить в соответствующих ветвях друг на друга с учётом их направлений, то получим действительные токи I1, I2, Iн в соответствующих ветвях схемы (см. рис.10а).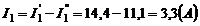 
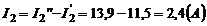
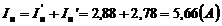
Точно также находятся напряжения на отдельных участках цепи, например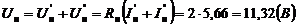 
.
Список литературы
1. Лоторейчук, Е. А.Теоретические основы электротехники [Text]: учебник / Е.А. Лоторейчук. - М.: ИД "ФОРУМ", ИНФРА-М, 2014. - 320 с.: ил. - ISBN 978-5-8199-0040-6 ИД ("ФОРУМ"). - ISBN 978-5-16-000986-5 (ИНФРА-М): 460.00. Кол-во экземпляров: 60.
2. Новожилов, О. П. Электротехника и электроника [Text]: учебник для бакалавров / О.П. Новожилов. - М.: Юрайт, 2012. - 653 с. - (Бакалавр). - ISBN 978-5-9916-1450-4: 492.47. Кол-во экземпляров: 10.
3. Бутырин, П. А. Электротехника [Text]: учебник / П.А. Бутырин, О.В. Толчеев, Ф.Н. Шакирзянов; под. ред. П.А. Бутырина. - 7-е изд., испр. - М.: Академия, 2010. - 272 с. - ISBN 978-5-7695-7352-1: 275.00. Кол-во экземпляров: 10.
4. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1.-4-е изд. /К.С. Демирчан, Л.Р. Нейман, Н.В.Коровкин, В.Л.Чечурин.- СПб.: Питер, 2004. – 463 с.: ил. (и предыдущие издания). Кол-во экземпляров: 12.