Построение графиков частотных характеристик

Частотные характеристики электрических цепей

Если в состав цепи входят реактивные элементы(L, C), то из-за зависимости их сопротивлений от частоты гармонического сигнала параметры цепи становятся частотно-зависимыми. Зависимости параметров цепи от частоты гармонического воздействия называют частотными характеристиками, т.е. для каждого параметра цепи есть своя комплексная частотная характеристика (КЧХ). Названия частотным характеристикам дают в соответствии с названием параметра. Частотная характеристика цепи или комплексная функции цепи есть зависимость от частоты отношения комплексных амплитуд отклика и воздействия. Она может быть записана в показательной и алгебраической форме:

где - амплитудно-частотная характеристика (АЧХ) (или модуль комплексной функции - |H(jw)|) - есть зависимость от частоты отношения амплитуд выходного и входного гармонических колебаний;

j(w)=arctg[Jm[H(jw)] - фазо-частотная характеристика (ФЧХ) (или аргумент комплексной функции – arg(H(jw)) - есть зависимость от частоты разности фаз выходного и входного сигналов т.е. j(w)=j₂-j_1.

Re[ H(jw)]. Im[H(jw)] – реальная и мнимая части комплексной функции.

Расчет частотных характеристик

В основу расчета частотных характеристик положен метод комплексных амплитуд (МКА). Для простых цепей частотную характеристику находят, используя законы Ома и Кирхгофа. Для сложных функций при расчете частотных характеристик используют методы: эквивалентных преобразований, контурных токов, узловых потенциалов и др. Порядок применения метода МКА следующий:

1. Гармонические токи и напряжения (x(t)=X_mcos(ωt-φ_x)) всех ветвей схемы заменить их комплексными амплитудами (X_m=X_me^-jφx), а от исходной схемы цепи составленной из элементов (R, L, C), перейти к комплексной схеме замещения с комплексными сопротивлениями (Z _R=R, Z _C=1/(jωC), Z _L= jωL).

2. Составить уравнения электрического равновесия цепи для комплексных изображений токов и напряжений с использованием законов Ома и Кирхгофа или используя другие методы.

3. Решить систему составленных уравнений относительно комплексных амплитуд интересующих токов или напряжений (Ý_m=Y_me^-jφx).

4. Для нахождения комплексной частотной характеристики (КЧХ) записать отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.

5. Если необходимо, то перейти от комплексных амплитуд интересующих токов и напряжений к гармоническим функциям времени (y(t)=Y_mcos(ωt-φ_y)).

Для цепи второго порядка КЧХ в общем случае можно записать в виде

. (1.11)

Выделим в числителе и знаменателе действительную и мнимую части, приведем подобные члены, и запишем 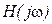в показательной форме

. (1.12)

Отсюда получим выражения для расчета амплитудно-частотных (АЧХ) и фазо-частотных (ФЧХ) характеристик

(1.13)

φ(ω)=φ_числ(ω)–φ_знам(ω), (1.14)

Построение графиков частотных характеристик

При графическом изображении частотных характеристик электрической цепи обычно строят отдельные графики АЧХ и ФЧХ цепи. Графики функции, заданной формулой Н(ω) строятся по точкам, в определенном диапазоне частот, в котором проявляются основные свойства электрической цепи, которые затем соединяются плавной линией.

Выбор диапазона частот.

Для оценки частотного диапазона, в котором необходимо построить графики частотных характеристик цепи, определим особые точки операторной передаточной функции. Для этого заменим в формуле (1.11) =p, получим операторный коэффициент передачи по напряжению

. ()

Особыми точками (нулями и полюсами) K_u(p) являются значения аргумента (нули), при которых M(p)=0, и значения аргумента (полюсы), при которых N(p)=0, где i=1,2.. порядковый номер особой точки. Для наглядности их изображают в комплексной плоскости, комплексной частоты р=a+jw. Нули изображают кружочками, а полюсы крестиками.

За частотный диапазон можно принять интервал между и

; ,

где - расстояние от начала координат до ближайшей особой точки, которое определяется ее модулем, т.е. =min{| |,| |}; - расстояние до самой удаленной особой точки, т.е. =max{| |,| |}, где модуль комплексной частоты определяют по формуле |p|= .

Выбор масштаба построения графиков. При построении графиков частотных характеристик применяют различные масштабы по осям (вертикальной – ось ординат и горизонтальной – ось абсцисс): абсолютный (линейный) масштаб по осям применяют, если диапазон изменения величины не более одной декады, и логарифмический, если диапазон изменения величины составляет две и более декады. На практике часто используется полулогарифмический масштаб, когда по горизонтальной оси берется логарифмический масштаб, а по вертикальной – линейный.

В тех случаях, когда предполагаемая частотная характеристика располагается в широком диапазоне частот, то ее график строят в логарифмическом масштабе по оси частот. Сначала проводят расчет точек на частотах f→0, f→∞, а далее, на частотах в логарифмическом масштабе `f =lg(f/f<sub>0</sub>), где`f=1,2, 3 и т.д. – нормированная частота в логарифмическом масштабе; f₀ – частота излома (частота среза) характеристики, выбранная за единицу; f/f₀=f_н - нормированная частота в абсолютном масштабе. Величина f₀ может быть принята любой. В простейшем случае за f₀ можно принять 1Гц, или 1кГц. Однако если анализируется цепь первого порядка, то за f₀ принимают f₀=(2pt)^-1 (w₀=1/t), где t - постоянная времени цепи.

Если цепь имеет несколько постоянных времени, то ее ассимптотическая логарифмическая характеристика, состоит из нескольких прямых и имеет несколько точек излома, каждой из которых соответствует своя постоянная времени t₁=1/w₁; t₂=1/w₂ и т. д. Выбрав одну из них за опорную, можно построить график в масштабе wt или lgwt.

При построении логарифмических частотных характеристик, более подробно, в каждой декаде следует брать по 3 –точки (0, 2, 5). Если необходимо, то проводят уточнение вблизи точек экстремумов - минимума или максимума, взяв по 10 точек вблизи них.

Особенности построения графиков ФЧХ.

Формула ФЧХ (уравнение ФЧХ) выражает зависимость аргумента (фазового угла) комплексной функции Кu(j ω ) от частоты:

φ(ω)=φ_числ(ω)–φ_знам(ω), (7)

где φ _числ(ω) - аргумент числителяН(jω), φ _знам(ω) - аргумент знаменателяН(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z =А(ω)+jВ(ω) вычисляется по различным формулам в зависимости от положения комплексного числа на комплексной плоскости (см. табл. 1.1).

Таблица 1.1.

«№	Область расположения числа Z=А+jВ на комплексной плоскости.	Условия	Формула φ (ω)
1)		A(ω) > 0, B(ω) > < 0.
2)		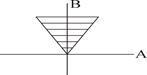B(ω) > 0, A(ω) > < 0.
3)		B(ω)£ 0, A(ω) > < 0.
4)		A(ω) < 0, B(ω)> 0.
5)		A(ω) < 0, B(ω) < 0.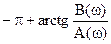

Отсюда следует, что уравнение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.

Рассмотрим первый пример. Для схемы 3 приведенной в табл.3.2 частотная характеристика коэффициента передачи имеет вид:

К(jω)= {(jω)²R₁C₁R₂C₂}/{(1+(jω)²R₁C₁R₂C₂)+ jω(R₁C₁+R₂C₂+R₁C₂)}=

= {А(ω)}/{С(ω)+ jD(ω)},

где А(ω)=-(ω)²А₁; С(ω)= 1-(ω)²А₁; D(ω)= ωВ₁, А₁= R₁C₁R₂C₂, В₁=R₁C₁+R₂C₂+R₁C₂.

Формула ФЧХ вычисляется из выражения

φ(ω)=φ_числ(ω)–φ_знам(ω),

1. Анализ числителя для определения его аргумента.

Действительная часть числителя при любой частоте А(ω)=-(ω)²А₁<0 - отрицательна, а мнимая часть отсутствует т.е. всегда равна нулю В(ω)=0. Следовательно, точка отображающая числитель всегда находится на отрицательной части реальной оси т. е.

φ_числ(ω)=π.

2. Анализ числителя для определения его аргумента.

Мнимая часть знаменателя при любой частоте положительна, а действительная знакопеременная, следовательно точка отображающая знаменатель находится в первом или втором квадранте комплексной плоскости и для вычисления аргумента знаменателя нужно использовать формулу 2 из таблицы1.1.

φ_знам(ω)= π/2 - arctg((1-ω² А₁)/ ω В₁).

Таким образом окончательно, ФЧХ коэффициента передачи для нашего примера имеет вид

φ(ω)= π- (π/2 - arctg((1-ω²А₁)/ ωВ₁))= π/2 + arctg((1-ω²А₁)/ ωВ₁)).

Рассмотрим второй, более сложный, пример. Частотная характеристика цепи задана выражением

. (9)

где A(ω)=(10¹⁰–ω ²), B(ω)=0, C(ω)=(10¹⁰ –ω ²), D(ω)=0.3636·10⁵ω.

Учитывая (8), получим выражение для АЧХ

(10)

 

Формула ФЧХ выражает зависимость аргумента (фазового угла) комплексной функции K_U(jω) от частоты и имеет вид:

 

(11)

где φ _числ(ω) – аргумент комплексного числителяH(jω),

φ _знам(ω) – аргумент комплексного знаменателяH(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z(jω)=А(ω)+jB(ω) вычисляется различным образом в зависимости от положения комплексного числа на комплексной плоскости (см. таблицу 1.1).

Отсюда следует, что выражение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива в некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.

Для нашего примера действительные A(ω) и C(ω) и мнимая D(ω) части числителя и знаменателя коэффициента передачи (9) зависят от частоты и не только меняют свое значение, но и меняют знак. А это значит, что комплексные числа числителя и знаменателя меняют свое положение на комплексной плоскости. Это обстоятельство требует анализа аргументов числителя φ_числ(ω) и знаменателя φ_знам(ω) при изменении частоты от нуля до бесконечности.

1. Анализ числителя для определения его аргумента.

Действительная часть числителя равна A(ω)=10¹⁰–ω². Если , т.е. , числитель представляет собой действительное и положительное число – A(ω) ≥ 0. Поэтому φ _числ( ω )= 0 при .

При , A(ω) < 0. Поэтому φ _числ( ω )= .

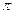2. Анализ знаменателя для определения его аргумента.

Действительная часть знаменателя равна действительной части числителя C(ω)=A(ω)=10¹⁰–ω² и изменяется с изменением частоты также, как и числитель. Мнимая часть знаменателя D(ω)=0.3636·10⁵ω прямо пропорциональна частоте ω и положительная D(ω)> 0 при ω > 0.

При точка, отображающая знаменатель, находится в первом квадранте комплексной плоскости, причем при ω>0.8346 10⁵ она пересекает биссектрису первого квадранта. Поэтому в диапазоне 0< ω<0.8346·10⁵ при вычислении фазового угла знаменателя нужно использовать формулу 1 из таблицы 1: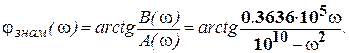

При 0.8346·10⁵ <ω 1.1982·10⁵ отображающая точка находится в области 2 таблицы 1. Поэтому

При ω >1.1982·10⁵ точка переходит в область 4 таблицы 1.

Таким образом, ФЧХ коэффициента передачи в нашем примере будет описываться различными формулами для четырех частотных областей.