Кг хлеба, 4 л молока, 1 кг сахара.
В этом случае второй закон Госсена выполняется: 5/2 = 7/2,8 = 10/4.
Общая полезность этого набора:
15 + 10 + 8 + 7 + 5 + 12 + 11 + 10 + 7 + 10 = 95
превышает общую полезность купленного Максимом набора:
15 + 10 + 8 + 12 + 11 + 10 + 7 + 10 + 8 = 91.
|
|
| Задача №6.7.1
Как изменились цены, если прямая бюджетного ограничения сдвинулась таким образом, как это изображено на рисунке.
Прокомментируйте каждый изображённый на рисунке случай
(в первом ряду – случаи а) и б))?
а) Цена одного товара увеличилась.
б) Цены обоих товаров снизились в два раза.
в) Цена одного товара выросла, а другого снизилась.
г) Цена одного товара снизилась.
Решение
В данной задаче важно понимать, что снижение цен ведёт к росту покупательной способности того же дохода, а рост цен – к снижению его покупательной способности, поэтому в первом случае бюджетная линия смещается вправо и вверх, во втором случае – влево и вниз. Если цена меняется только на один товар, то смещается только соответствующая часть бюджетной линии.
|
|
| Задача №6.7.2
Опишите, опираясь на данные графика, предпочтения Робинзона.
Ответ
Робинзон может проводить время, бездельничая на пляже и, тем самым, потребляя досуг или же собирая кокосы. Чем больше он соберет кокосов, тем больше у него будет еды, но тем меньше времени останется на улучшение загара. Предпочтения Робинзона в отношении кокосов и досуга изображены на рисунке. Они имеют точно такой же вид, как предпочтения в отношении досуга и потребления, за исключением того, что теперь мы откладываем по горизонтальной оси труд, а не доход.
|
|
| Задача №6.7.3
Функция полезности ТU = 5х + 4y + 6z, доход потребителя равен 60, цены продуктов X, Y и Z равны 3, 2 и 9 соответственно. Найдите равновесный набор.
Решение
1) Отношение предельной полезности к цене равно: 5/3 для продукта X, 4/2 для продукта Y, 6/9 для продукта Z. Эти числа различны. Касания нет.
2) В этом случае равновесным является набор на бюджетной плоскости, в котором имеется только продукт с наибольшим отношением предельной полезности к цене. Таким продуктом является Y, так как 4/2 > 5/3 и 4/2 > 6/9.
Ответ:набор (0; 30; 0) – равновесный.
|
|
| Задача №6.7.4
Функция полезности ТU = ху, доход потребителя – 24, цены продуктов Х и Y равны 2 и 3 соответственно. Найдите равновесный набор.
Решение
1) Найдем формулу для предельной нормы замещения продукта X.
Так как MUХ = у и MUY = х, то MRS = у/х. В точке равновесия y/х = 2/3.
2) Запишем бюджетное ограничение: 2х + 3у = 24.
Составим систему двух уравнений из соотношений, полученных в предыдущих пунктах. Ее решение: х = 6, у = 4 – равновесный набор.
Максимальное значение полезности равно 6 * 4 = 24.
Ответ: х = 6, у = 4 – равновесный набор.
|
|
| Задача №6.7.5
Некто потреблял 5 шт. товара А, приносящего ему 8 ед. полезности, и 12 шт. товара Б, дающего 18 ед. полезности. Он решил, что ничего не произойдет, если он будет потреблять 7 шт. товара А и 10 шт. товара Б, которые принесут ему, соответственно 10 и 16 ед. полезности.
Определить величины предельной полезности для каждого товара и предельную норму замещения товаров.
Решение
MU А = (10 – 8)/(7 – 5) = 1
MU Б = (18 – 16)/(12 – 10) = 1
MRS А/Б = 1.
|
|
| Задача №6.7.6
Студент потребляет в месяц 2 кг сосисок по цене 141 руб. за 1 кг и 4 буханки хлеба по цене 12 руб. за одну буханку.
Чему равна предельная норма замены сосисок хлебом в состоянии равновесия?
Решение
В состоянии равновесия отношения предельных полезностей равно отношению цен товаров:
MRSc,х = |– С / + X| = MUx / MUc = Рх / Рс,
где С – количество сосисок; Х – количество хлеба;
MUx; MUc – предельные полезности хлеба и сосисок.
MRSc, х – предельная норма замены.
Поскольку Рс = 141, а Рх = 12, то MRSc,х = 12 /141.
|
|
| Задача №6.7.7
За месяц студент расходует на апельсины и бананы 100 рублей.
Цена одного апельсина равна 5 руб., а цена одного банана – 2 руб.
Какое количество апельсинов и бананов потребляет рациональный студент в месяц, если общая полезность от количества потребляемых фруктов составляет TU(x,y) = 10XY, где X и Y количество апельсинов и бананов соответственно.
Решение
Выбор студента предопределён бюджетным ограничением:
100 = 5Х + 2Y;
В состоянии равновесия отношение предельных полезностей продуктов равно отношению цен на них:
MU(x) / MU(y) = Рх / Ру;
Найдём значения предельных полезностей потребляемых товаров:
TU(x, у)’х = MU(x) = 10Y;
TU(x, у)’у = MU(y) = 10Х.
Согласно теории потребления, рациональный студент должен достичь максимума совокупной полезности от количества потребляемого продукта в точке касания кривой безразличия с линией бюджетного ограничения.
Поэтому составим и решим систему уравнений:
5Х + 2Y = 100,
10Y / 10Х = 5/2.
Таким образом X = 10, a Y = 25,
т.е. рациональный студент потребляет за месяц 10 апельсинов и 25 бананов.
|
|
Задача №6.7.8
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение
В точке оптимума выполняется равенство:
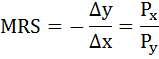По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5 = 4.
Найдём доход индивида, используя бюджетное ограничение:
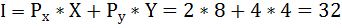где: I – доход, Рх и Ру – цены двух рассматриваемых благ, Х и Y – их количества.
|
|
| Задача №6.7.9
Максим составил для себя таблицу полезности трех благ.
Имея 25,2 ден. ед., он купил 3 кг хлеба по цене 2 руб. за 1 кг, 4 л молока по цене 2,8 руб. за 1 л и 2 кг сахара по цене 4 руб. за 1 кг.
1. Доказать, что Максим не достиг максимума полезности при своем бюджете.
2. Какой набор благ обеспечивает Максиму максимум полезности при его бюджете?
Номер Вид блага, ютили
порции Хлеб Молоко Яблоки
I 5 12 10
II 10 11 8
III 8 10 6
IV 7 7 3
V 5 6 1
Решение
1. Ассортимент купленных Максимом благ не удовлетворяет второму закону Госсена:
8/2 ≠ 7/2,8 ≠ 8/4; поэтому максимум полезности не достигнут.
2. За счет перераспределения денег с самой нерентабельной покупки – 2-го кг сахара на самую рентабельную покупку хлеба можно приобрести следующий набор:
5 кг хлеба, 4 л молока, 1 кг сахара.
В этом случае второй закон Госсена выполняется: 5/2 = 7/2,8 = 10/4.
Общая полезность этого набора: 15 + 10 + 8 + 7 + 5 + 12 + 11 + 10 + 7 + 10 = 95
превышает общую полезность купленного Максимом набора:
15 + 10 + 8 + 12 + 11 + 10 + 7 + 10 + 8 = 91
|
|
| Задача №6.7.10
Функция полезности потребителя описывается формулой U = XY/2,
где X – объем потребления бананов, Y – объем потреб ления пепси-колы.
Цена 1 кг бананов 3 руб., 1 л пепси-колы стоит 2 руб.
Летом потребитель тратил на эти товары 20 руб. в неделю. Зимой цена бананов поднялась до 5 руб. за килограмм, цена пепси-колы не изменилась.
Определите: а) Объем оптимального потребления бананов и пепси-колы летом. б) Величину расходов, необходимую зимой для достижения того же уровня полезности, что и летом. в) Количественное значение эффекта дохода и эффекта замещения.
Решение
а) Поскольку 3Х + 2Y = 20, а Y/X = – 3/2,
то оптимальное потребление составит 3,3 кг бананов и 5 л пепси-колы.
б) Зимой оптимальный потребительский набор составит:
2,6 кг бананов и 6,5 л пепси-колы, на его покупку будет затрачено 26 руб.
в) Эффект замещения составит – 0,7 кг бананов и 1,5 л пепси-колы.
Если бы покупатель тратил зимой на покупки 20 руб, то его оптимальный набор составил бы 2 кг бананов и 5 л пепси-колы.
Следовательно, эффект дохода составляет 0,6 кг бананов и 1,5 л пепси-колы.
|
|
| Задача №6.7.11
Предельная полезность масла для француза зависит от его количества:
MU = 40 – 5QM, где QM – количество масла, в кг; MUM – предельная полезность масла.
Предельная полезность хлеба равна: MUx = 20 – 3Qx,
где Qx – количество батонов хлеба; MUX – предельная полезность хлеба.
Цена килограмма масла равна 5 франкам, цена батона хлеба – 1 франку.
Общий доход потребителя составляет 20 франков в неделю.
Какое количество хлеба и масла потребляет француз?
Ответ. Масла – 3 кг, хлеба – 5 батонов.
|
|
| Задача №6.7.12
Эластичность спроса на концерты по цене для Маши равна -1.
Эластичность ее спроса по доходу составляет 3.
Перекрестная эластичность по цене между концертами и бассейном равна -2.
В 1995 г. Маша посетила 100 концертов. В 1996 г. цена билета на концерт возросла на 15%, цена одного посещения бассейна упала на 5%, а доход Маши возрос на 10%.
Какое количество концертов посетит Маша в 1996 г.?
Решение
1) ΔQ% = -1*15 = -15%;
2) ΔQп% = -2*5 = -10%;
3) ΔQ% = 3*10 = +30%.
Всего ΔQ% = -15 - 10 + 30 = + 5%. Qк = 105 концертов
|
|
| Задача №6.7.13
Потребитель тратит 20 руб. в день на апельсины и яблоки.
Предельная полезность яблок для него равна 20 – 3х, где X – количество яблок, в шт.
Предельная полезность апельсинов: 40 – 5у, где Y – количество апельсинов, в шт.
Цена одного яблока составля ет 1 руб., цена одного апельсина – 5 руб.
Какое количество яблок и апельсинов купит рациональный потребитель?
Решение
1) В состоянии равновесия отношение предельных полезностей равно отношению цен товаров MUх / MUу = Рх / Ру
2) Выбор потребителя предопределен бюджетным ограничением:
Рх * X + Ру * Y = 1.
3) Поэтому: (20 – 3х) /(40 – 5у) = 1 / 5; х + 5у = 20.
Решая систему уравнений, получаем ответ: х = 5, у = 3.
|
|
Задача №6.7.14
Заполните таблицу.
Госпожа N любит как кино, так и театр. В таблице показана полезность, которую она получает от потребления того и другого блага в разных количествах.
Пусть цена театральных билетов равна $7,5, а цена билетов в кинотеатр равна $1,5.
Обычно госпожа N за осень ходит дважды в театр и 10 раз в кино.
Таблица
| Количество
| Кино
| Театр
| | общая полезность
(ед.)
| предельная
полезность
(ед.)
| MU/P
| общая полезность
(ед.)
| предельная
полезность
(ед.)
| MU/P
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| | | | | | | | | Пользуясь данными таблицы, ответьте на следующие вопросы.
| Вопросы
| | а) Сколько денег тратит госпожа N на удовлетворение
своих духовных потребностей за осень?
б) Какую полезность она получает от собственного потребления?
в) Какова предельная полезность, которую она получает от кино и театра?
г) При какой комбинации услуг театра и кино
полезность окажется максимальной?
д) Какую полезность получит госпожа N, если весь бюджет будет тратить на театр?
| |
|
Задача №6.7.15
В набор потребителя входят два товара: минеральная вода и печенье.
Предельная полезность характеризуется следующими данными:
| Количество минеральной воды
|
|
|
|
|
|
| | Предельная полезность (MU)
|
|
|
|
|
|
| | Количество печенья
|
|
|
|
|
|
| | Предельная полезность (MU)
|
|
|
|
|
|
|
Цена одной бутылки минеральной воды 10 ден. ед.,
цена одной пачки печенья – 5 ден. ед.
Общий доход потребителя, который он тратит на минеральную воду и печенье, равен 25 ден. ед.
Какое количество минеральной воды и печенья покупает рациональный потребитель?
Дано:
Рх = 10 ден. ед.
Ру = 5 ден. ед.
I = 25 ден. ед.
Найти: параметры рационального выбора.
Решение
Потребителький выбор – это выбор, максимизирующий функцию полезности рационального потребителя в условиях ограниченности ресурсов (денежного дохода). Функция полезности максимизируется в том случае, когда денежный доход распределяется таким обоазом, что последняя денежная единица (рубль, евро и т. д), затраченная на приобретение любого блага, приносит одинаковую предельную полезность.
Равновесие потребителя соответствует следующему условию:
Рассчитаем значение предельно полезности на одну ден. ед.
| Количество минер. воды
| Предельная полезность
минер. воды на 1 ден. ед.
| Количество печенья
| Предельная полезность печенья на 1 ден. ед.
| |
|
|
| 1,4
| |
| 0,8
|
| 1,2
| |
| 0,6
|
|
| |
| 0,4
|
| 0,8
| |
| 0,3
|
| 0,6
| |
| 0,2
|
| 0,4
|
Этому равенству соответствует несколько комбинаций:
1 бутылка мин. воды и 3 пачки печенья;
2 бутылки мин. воды и 4 пачеи печенья;
3 бутылки минеральной воды и 5 пачек печенья;
4 бутылки минеральной воды и 6 пачек печенья,
но только одна комбинация входит в бюджет потребителя, а другие выходят за рамки данного бюджета.
С учетом бюджетного ограничения:
I = Px*Qx + Py*Qy
25 = 10*1 + 5*3
10 + 15 = 25
|
Поиск по сайту:
|
