Для того чтобы принимать разумное решение о долговременных инвестициях, вы должны учитывать как процентную ставку, так и уровень инфляции. Простые акции, дивиденды по которым не являются постоянной величиной, застрахованы от инфляции, так как с ростом ее темпов увеличивается и прибыль, из которой выплачиваются дивиденды. Кроме того, действенным средством страховки (хеджирования) против инфляции является выплата дивидендов в виде акций. По облигациям и сбережениям на счетах в банках выплачивается меньший доход по сравнению с простыми акциями, однако здесь и гораздо меньше риск потери первоначального капитала. Вместе с тем риск уменьшения покупательской способности денег вследствие инфляционного воздействия для всех видов инвестиций весьма высок.
Для учета соотношения между процентной ставкой и уровнем инфляции следует различать номинальную процентную ставку 
, выраженную в той или иной валюте без поправки на инфляцию, и реальную процентную ставку 
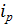, корректирующую номинальную на уровень инфляции.
Общая формула, отображающая соотношение реальной ставки доходности, номинальной процентной ставки и уровня доходности, имеет следующий вид:
или, соответственно,
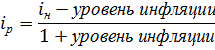
Если использовать соотношение годовых процентных ставок (АРR) с непрерывным начислением процентов, то последнее выражение принимает вид:
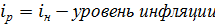
Так, если номинальная АРR 8% годовых и уровень инфляции 6% (с учетом непрерывного начисления), то реальная ставка будет равна 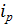= 8 – 6 = 2% годовых, начисляемых непрерывно.
Инструмент с фиксированным доходом, который в номинальном выражении является надежным, в реальном выражении несет определенную степень риска. Например, представим, что банк предлагает вкладчикам безрисковую годовую процентную ставку в размере 8%. Поскольку на текущий момент будущий уровень инфляции заранее неизвестен, в реальном выражении помещение денег на данный банковский счет будет рискованным.
|
|
Для нашего случая ожидаемая реальная ставка доходности будет:
или 1,89% годовых. Если же уровень инфляции окажется выше 6%, то и реальная ставка будет меньше 1,89%.
Инфляционная премия
Пусть первоначальная сумма 
при заданной ставке процентов превращается за определенный период в сумму 
, а в условиях инфляции она превращается в сумму 
, что требует уже иной процентной ставки.
Величина
называется темпом инфляции, а величина
называется индексом инфляции, то есть, если годовой уровень инфляции α, то через n лет первоначальная сумма превратится в 
, что то же самое, что наращение суммы Р по сложной годовой ставке процентов α.
Пример. Пусть цены каждый месяц растут на 2%. Банки и финансовые компании часто вовлекают клиентов в рискованные вклады, к примеру, под 25% годовых, приводя такие расчеты уровня инфляции: 2% · 12 = 24%; и вроде бы есть выгода. На самом деле за 12 месяцев цены вырастут в (1 + 0,02)^12 = 1,268 раз, то есть годовой темп инфляции составляет 1,268 – 1 = 0,268, или 26,8%.
Расчет показывает, что процентная ставка 25% годовых совсем не привлекательна и может лишь рассматриваться в плане минимизации потерь от инфляции.
Если простая годовая ставка ссудного процента равна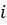 
, а ставка ссудного процента, учитывающая инфляцию — 
, то с одной стороны
а с другой стороны
Из уравнения эквивалентности
|
|
следует:
называемая формулой И. Фишера, в которой сумма (
) является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина называется инфляционной премией.
Формула Фишера позволяет избежать такой распространенной ошибки, когда для подсчета процентной ставки, учитывающей инфляцию, к величине реальной ставки доходности просто прибавляют величину темпа инфляции, т.е. если i = 20% и α = 10%, то за процентную ставку, учитывающую инфляцию, принимается сумма i + α = 0,2 + 0,1 = 0,3, или 30%. Однако сюда нужно добавить еще слагаемое, равное iα = 0,2 · 0,1 = 0,02, или 2%. Этот мно-житель, умноженный на десятки тысяч у.е., дает значительную добавку к сумме инфляции.