Знание функций спроса (8.5) и функции предложения (8.6) позволяет отслеживать реакцию производителя на изменение цены выпуска продукции ( ) и цен на ресурсы (
) и цен на ресурсы ( ,
,  ), а также определять их ценность, взаимозаменяемость и взаимодополняемость.
), а также определять их ценность, взаимозаменяемость и взаимодополняемость.
Пусть функции спроса на ресурсы

описывают оптимальное распределение ресурсов, при этом функция

есть функция предложения выпуска.
Введем обозначения  ,
,  матрица Гессе для ПФ
матрица Гессе для ПФ  (в силу ограничений матрица Гессе определенно-отрицательная и
(в силу ограничений матрица Гессе определенно-отрицательная и  ).
).
Следующая система уравнений в теории моделирования поведения производителя называется основным матричным уравнением теории фирмы:
 (8.9)
(8.9)
Она позволяет оценивать поведение производителя при одновременном изменение цены выпуска и цен на ресурсы.
Первое уравнение в системе (8.9) показывает, как изменится выпуск  при увеличении цены
при увеличении цены  на продукцию фирмы. Так как матрица Гессе определенно-отрицательная, то
на продукцию фирмы. Так как матрица Гессе определенно-отрицательная, то 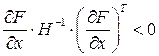 при всех
при всех  , т.е.
, т.е.  (с ростом цены
(с ростом цены  выпуск растет; выпуск как функция цены является возрастающей).
выпуск растет; выпуск как функция цены является возрастающей).
Второе уравнение в системе (8.9) позволяет оценить поведение функции спроса на ресурсы при увеличении цены выпуска  . При этом ресурс (например, капитал
. При этом ресурс (например, капитал 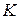 ) называется ценным (малоценным), если
) называется ценным (малоценным), если  (соответственно
(соответственно  ). Можно доказать, что обязательно среди двух ресурсов (капитала
). Можно доказать, что обязательно среди двух ресурсов (капитала 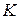 и труда
и труда  ) найдется, по крайней мере, хотя бы один ценный (при увеличении цены выпуска
) найдется, по крайней мере, хотя бы один ценный (при увеличении цены выпуска  увеличивается спрос на этот ресурс).
увеличивается спрос на этот ресурс).
Третье уравнение в системе (8.9) позволяет оценить поведение функции предложения 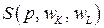 при изменении цен
при изменении цен  ,
,  на ресурсы, причем
на ресурсы, причем
 .
.
Возрастание цены  продукции приводит к повышению (понижению) спроса на отдельные виды ресурсов, если повышение цены на этот ресурс приводит к сокращению (возрастанию) оптимального выпуска. В частности, увеличение цены на малоценный ресурс ведет к увеличению выпуска.
продукции приводит к повышению (понижению) спроса на отдельные виды ресурсов, если повышение цены на этот ресурс приводит к сокращению (возрастанию) оптимального выпуска. В частности, увеличение цены на малоценный ресурс ведет к увеличению выпуска.
Четвертое уравнение в системе (8.9) позволяет выяснить, как ведут себя функции спроса на ресурсы при изменении цен  ,
,  на ресурсы. Имеем
на ресурсы. Имеем
 ,
,
причем  . Повышение цены на ресурс (капитал и труд) всегда приводит к падению спроса на этот ресурс (функции спроса как функции цен на ресурсы являются убывающими).
. Повышение цены на ресурс (капитал и труд) всегда приводит к падению спроса на этот ресурс (функции спроса как функции цен на ресурсы являются убывающими).
Ресурсы 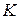 и
и  называются взаимозаменяемыми (взаимодополняемыми), если
называются взаимозаменяемыми (взаимодополняемыми), если  (соответственно
(соответственно  ). Для взаимозаменяемых ресурсов увеличение цены на один из них приводит к падению спроса на этот ресурс, но к увеличению спроса на другой. Для взаимодополняемых ресурсов увеличение цены на один из них приводит к одновременному падению спроса на оба ресурса.
). Для взаимозаменяемых ресурсов увеличение цены на один из них приводит к падению спроса на этот ресурс, но к увеличению спроса на другой. Для взаимодополняемых ресурсов увеличение цены на один из них приводит к одновременному падению спроса на оба ресурса.
Замечание 8.5.Система уравнений (8.9) применяется и в том случае, если не удалось в явном аналитическом виде найти функции спроса на ресурсы (8.5). В этом случае предполагается, что найдено оптимальное распределение ресурсов  (локальное рыночное равновесие) при наперед заданных ценах
(локальное рыночное равновесие) при наперед заданных ценах  ,
,  ,
,  . Тогда исследование проводится в окрестности точки
. Тогда исследование проводится в окрестности точки  .
.
Пример 8.3. Используя решение в среде Maple примера 8.2 (учитывая, что в явном виде найдены функции спроса на ресурсы и функция предложения), оценить поведение производителя при изменениях цен на ресурсы и цены продукции.
Рекомендуем самостоятельно составить программу в среде Maple для решения этого примера.
8.4. Минимизация издержек при постоянном уровне выпуска
Пусть заданы производственная функция  вида (8.1) функция затрат
вида (8.1) функция затрат  на ресурсы
на ресурсы 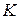 и
и  . Уровень производства задан величиной
. Уровень производства задан величиной  . Требуется найти точку
. Требуется найти точку  оптимального распределения ресурсов (называемую также точкой наиболее экономичного производства) такую, что при данном уровне выпуска
оптимального распределения ресурсов (называемую также точкой наиболее экономичного производства) такую, что при данном уровне выпуска  издержки
издержки  были минимальны:
были минимальны:
 (8.10)
(8.10)
Задача (8.10)  задача на условный экстремум, решаемая методом множителя Лагранжа. Вводится функция Лагранжа
задача на условный экстремум, решаемая методом множителя Лагранжа. Вводится функция Лагранжа

Необходимое условие точки условного экстремума имеет вид:

Пример 8.4. Используя ПФ CES предприятия из примера 8.2, найти точку  наиболее экономичного производства такую, что при уровне выпуска
наиболее экономичного производства такую, что при уровне выпуска  издержки
издержки  были минимальны.
были минимальны.
Решение. Программа в среде Maple имеет вид.
[> restart; with(Optimization): Digits:=6:
[> F:=A*(alpha*K^(-rho)+(1-alpha)*L^(-rho))^((-1)*g/rho);
C:=w[1]*K+w[2]*L; Pribyl:=P*F-C;


 [> A:=2.5: alpha:=1/3: rho:=-0.75: g:=0.75: w[1]:=1.5: w[2]:=2:
P:=6: Q[0]:=100:
[> F_Lagrang:=C+lambda*(Q[0]-F);
[> A:=2.5: alpha:=1/3: rho:=-0.75: g:=0.75: w[1]:=1.5: w[2]:=2:
P:=6: Q[0]:=100:
[> F_Lagrang:=C+lambda*(Q[0]-F);
 [> Gradient_F_Lagrang:={diff(F_Lagrang,K), diff(F_Lagrang,L),
diff(F_Lagrang, lambda)};
sys:={Gradient_F_Lagrang[1]=0, Gradient_F_Lagrang[2]=0,
Gradient_F_Lagrang[3]=0}:
Optimal_Raspred:=fsolve(sys, {K,L,lambda});
[> Gradient_F_Lagrang:={diff(F_Lagrang,K), diff(F_Lagrang,L),
diff(F_Lagrang, lambda)};
sys:={Gradient_F_Lagrang[1]=0, Gradient_F_Lagrang[2]=0,
Gradient_F_Lagrang[3]=0}:
Optimal_Raspred:=fsolve(sys, {K,L,lambda});

 [> K:=rhs(Optimal_Raspred[1]): L:=rhs(Optimal_Raspred[2]):
Minimum_C:=evalf(C); Maximum_Pribyl:=evalf(Pribyl);
[> K:=rhs(Optimal_Raspred[1]): L:=rhs(Optimal_Raspred[2]):
Minimum_C:=evalf(C); Maximum_Pribyl:=evalf(Pribyl);

 [> K:='K': L:='L':
[> Min_C:=evalf(Minimize(C, {F=Q[0]}, assume=nonnegative));
[> K:='K': L:='L':
[> Min_C:=evalf(Minimize(C, {F=Q[0]}, assume=nonnegative));
 [> Max_Pribyl=evalf(Maximize(Pribyl, {F=Q[0]},
assume=nonnegative));
[> Max_Pribyl=evalf(Maximize(Pribyl, {F=Q[0]},
assume=nonnegative));

|
§ 9. Моделирование рыночного равновесия
9.1. Понятие о рыночном равновесии
В § 7 была изучена модель поведения потребителя. Анализ модели показал, что если в многофакторной функции спроса меняется только цена  товара, а все остальные факторы (цены на другие товары, доход потребителя) неизменны, то функция спроса имеет вид
товара, а все остальные факторы (цены на другие товары, доход потребителя) неизменны, то функция спроса имеет вид  (функция монотонно убывает).
(функция монотонно убывает).
В § 8 изучалась модель поведения производителя, которая позволяла построить функцию предложения. Анализ показал, что если изменяется только цена  данного товара, а все остальные факторы (цены на другие товары, основные производственные фонды) остаются постоянными, то функция предложения имеет вид
данного товара, а все остальные факторы (цены на другие товары, основные производственные фонды) остаются постоянными, то функция предложения имеет вид  (функция монотонно возрастает).
(функция монотонно возрастает).
Функции спроса  и предложения
и предложения  являются основными составляющими модели рынка товаров, так как они являются решениями оптимизационных задач (см. § 7, § 8), которые возникают перед участниками.
являются основными составляющими модели рынка товаров, так как они являются решениями оптимизационных задач (см. § 7, § 8), которые возникают перед участниками.
Пересечение графиков функций спроса и предложения происходит в точке  (см. рис. 9.1), называемой точкой рыночного равновесия. Цену (см. рис. 9.1), называемой точкой рыночного равновесия. Цену  , при которой достигается состояние рыночного равновесия, называют равновесной ценой. При этом при фиксированной равновесной цене , при которой достигается состояние рыночного равновесия, называют равновесной ценой. При этом при фиксированной равновесной цене  потребитель, стремясь максимизировать свою полезность, предъявляет спрос потребитель, стремясь максимизировать свою полезность, предъявляет спрос  ; товаропроизводитель, максимизируя прибыль, поставляет на рынок товар в количестве ; товаропроизводитель, максимизируя прибыль, поставляет на рынок товар в количестве  . .
|  Рис.9.1.
Рис.9.1.
|
Равновесная цена  находится как решение уравнения
находится как решение уравнения
 .
.
Если параметры уравнения  не зависят явно от времени, то его называют статической моделью «спрос-предложение », в противном случае – динамической моделью «спрос-предложение ».
не зависят явно от времени, то его называют статической моделью «спрос-предложение », в противном случае – динамической моделью «спрос-предложение ».
Замечание 9.1. Помимо прямых функций спроса, полученных в § 7, в экономико-математических моделях часто используются так называемые логистические функции спроса от дохода потребителя [7]. На их основе можно получить следующие функции спроса  от цены
от цены  :
:

В данном пособии при составлении модели рыночного равновесия используем дискретные модели, когда переменные на промежутке времени  принимаются постоянными, равными
принимаются постоянными, равными
 .
.
Дискретные модели более актуальны в экономической ситуации, так как в них последовательно отражаются процедуры принятия решений.
Замечание 9.2. Для исследования дискретной модели «спрос-предложение» на устойчивость вводится понятие эластичности функций спроса  и предложения
и предложения  по цене
по цене  [2, 3, 8]:
[2, 3, 8]:

Замечание 9.3. В случае, когда функции спроса и предложения линейно зависят от цены  :
:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
мы имеем так называемую статическую модель Эванса [2, 3, 8].
9.2. Дискретные паутинообразные модели