§ 1. Математическая система Maple: основные принципы работы
Система Maple (разработана канадской компанией Waterloo Maple Software) на сегодняшнее время является одной из ведущих вычислительных систем компьютерной математики (наряду с MathCad, MathLab, Mathematica). По сути, Maple – это не просто математическая программа, а целый комплекс так называемых пакетов (packages), каждый из которых направлен на решение различных задач линейной алгебры, аналитической геометрии, математического анализа, дифференциальных уравнений, математической статистики, линейного и нелинейного программирования и т.д.
Maple традиционно считают системой аналитико-символьных вычислений (в отличие от нее MathCad – в основном программа для численных расчетов). Это означает, что система в большинстве случаев выдает ответ на решение задачи в самом общем – символьном виде. Maple одна из самых надежных идостоверных систем компьютерной математики. Надежных – в смысле высокой достоверности и точности полученных результатов при самых сложных символьных вычислениях.
Особенно эффективно использование Maple при обучении математике. Высочайший «интеллект» этой системы символьной математики объединяется в ней с мощными средствами математического численного моделирования и возможностями графической визуализации решений.
Maple – интегрированная система. Она объединяет в себе:
- мощный язык программирования, основанный на языке С++ (он же язык для интерактивного общения с системой);
- редактор для подготовки и редактирования документов и программ;
- современный многооконный пользовательский интерфейс с возможностью работы в диалоговом режиме;
- мощную справочную систему [меню Help, вкладки Introduction (общая справочная система), Topic Search… (поиск справки по какому-то определенному разделу или команде), Glossary (глоссарий)];
- ядро алгоритмов и правил символьных и аналитических преобразований математических выражений;
- численный и символьный процессоры;
- систему диагностики ошибок при вычислениях и преобразованиях;
- библиотеки встроенных и дополнительных процедур и функций;
- пакеты (packages) внешних функций для решения различного рода задач и поддержи других языков программирования и программ.
Рассмотрим кратко основные принципы работы в Maple. Более подробную информацию можно взять в [1, 9, 12, 13], а также на многочисленных сайтах, посвященных этой системе.
Основой для работы с символьными преобразованиями в Maple является ядро системы. Оно содержит сотни базовых функций и алгоритмов численных и символьных преобразований. В ядре имеются также библиотека операторов, команд и специально подключаемые пакеты (packages).
При первоначальном запуске появляется рабочее окно программы Maple (см. рис. 1.1).

Рис. 1.1.
В некоторых новых версиях программы оно может несколько отличаться от этого (в данном пособии речь идет о версии Maple 12, большинство примеров и описаний идут корректно на версиях Maple 10 и Maple 11). Рабочее окно программы состоит из следующих элементов:
1) основного (главного) меню (вкладки File, Edit, View, Insert, Format, Spreadsheet, Window, Help);
2) панели главных инструментов;
3) контекстной панели инструментов;
4) рабочей области (окно ввода и редактирования документов).
Рабочий лист (worksheet) среды является основным документом, в котором вводятся команды пользователя и в который выдаются результаты работы.
В рабочем листе Maple выделяются области ввода и области вывода. В области ввода пользователем вводятся команды (более подробное описание видов команд смотри далее), а также комментарии и текстовая информация. В полях вывода отображаются результаты выполнения введенных команд, включая сообщения об ошибках и графика. Комментарии и текстовая информация ядром Maple не обрабатываются и предназначены только для разработчиков и пользователей программ.
Основной режим работы системы Maple – командно-диалоговый режим. Это означает, что пользователь на запрос системы
[ >
должен ввести команды, понятные процессору Maple. Признаком окончания ввода команды служит символ точка с запятой (;) (результат действия процессора и вычисления будет выведен на экран) или символ двоеточие (:) (вычисления не будут выведены на экран, данный символ используется как знак разделителя при записи некоторых команд в одной строке).
Область ввода и соответствующая ей область вывода называются группой вычислений. На рабочем листе она отмечается квадратной скобкой слева. В группе вычислений может содержаться несколько областей ввода и вывода: все команды и операторы в областях ввода одной группы вычислений обрабатываются системой за одно обращение по нажатию клавиши <Enter>.
Maple имеет следующие основные виды команд:
1) оператор присваивания. Имеет следующий синтаксис (правило описания):
[ > имя_переменной:=значение[;\:]
Например,
[ > x:=3; v:=vector([1,2,3]); f(y):=sin(ln(y));


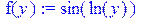
2) вызов процедуры или функции. Имеет следующий синтаксис:
[> имя_процедуры(список параметров)[;\:]
или
[> имя_переменной:=имя_функции(список параметров)[;\:]
В следующих строках определены функция  , дробно-рациональная функция
, дробно-рациональная функция 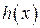 , процедуры интегрирования функции
, процедуры интегрирования функции  , дифференцирования
, дифференцирования 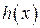 и функция упрощения производной от
и функция упрощения производной от 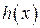 :
:
[ > restart; f(x):=tan(x); g(x):=int(f(x),x);


[ > h(x):=(x+2)/(x-2); diff(h(x),x); R:=simplify(diff(h(x),x));
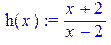


Приведем описание некоторых встроенных функций элементарных преобразований, которые нам потребуются в дальнейшем:
restart – “обнуление” значений всех переменных, отмена подключенных пакетов и т.д. (рекомендуется использовать в качестве первой команды рабочего листа);
evalf – преобразования числа в число с плавающей точкой (перевод точного числа в приближенное). Имеет следующий синтаксис:
[> evalf(<выражение>, <кол_цифр>);
[> evalf[<кол_цифр>](<выражение>);
Здесь параметры:
<выражение> – выражение, в котором все числа требуется привести к виду чисел с плавающей точкой;
<кол_цифр> – целое число, указывающее количество значащих цифр для вычислений (необязательный параметр);
Digits – глобальная переменная пакета Maple, значение которой (по умолчанию оно равно 10) показывает количество значащих цифр, выводимых на экран;
% (символ процента) – вывод результата выполнения предыдущей операции;
%% – вывод результата выполнения “предпредыдущей” операции;
# (символ решетка) – использование комментария в программе;
simplify – упростить выражение. Имеет следующий синтаксис:
[> simplify(<выражение>);
С полным списком функций, входящих в ядро Maple, и их обозначениями можно познакомиться, набрав команду inifcn, выделить ее мышкой и нажать кнопку <F1>;
3) подключение специальных пакетов Maple. Подключение пакета осуществляется следующим образом:
[> with(имя_пакета)[;\:]
Например, с помощью следующих команд:
[> restart; with(LinearAlgebra):
[> with(simplex);

в оперативную память загружаются пакет LinearAlgebra, ориентированный на решение задач линейной алгебры, и пакет simplex, предназначенный для решения задач линейного программирования.
Напомним, что при начальном запуске системы в оперативную память загружено только ядро системы. Однако при решении огромного класса задач, требующих сложных расчетов, встроенных процедур и функций ядра не хватает. В состав Maple 12 входит около 80 пакетов. Дадим список наиболее часто используемых пакетов Maple (с полным списком пакетов можно ознакомиться, используя главное меню Help –> вкладка Introduction –> Mathematics… –> Packages…):
· DEtools – решение обыкновенных дифференциальных уравнений и систем в численном и аналитическом видах, представление результатов в виде фазовых портретов, полей направлений, интегральных кривых и т.д.;
· finance – пакет финансовой математики;
· geom3d, geometry – пакеты трехмерной и двумерной евклидовой геометрии;
· LinearAlgebra – линейная алгебра (основной и незаменимый пакет для решения задач линейной и матричной алгебры);
· linalg – линейная алгебра и структуры данных массивов (до версии 6.0 являлся основным пакетом для решения задач линейной алгебры);
· inttrans – интегральные преобразования и их обратные преобразования;
· networks – пакет для работы с графами;
· numapprox – численная аппроксимация;
· Optimization – пакет для решения задач нелинейного программирования;
· plots – пакет для расширения графических возможностей;
· powseries – разложение функций в степенные ряды;
· simplex – пакет для решения задач линейного программирования;
· statistic – пакет для обработки статистических данных;
· sumtools — числовые ряды;
4) вызов справки (или примера) по определенному разделу, процедуре, функции, пакету. Вызов производится следующим образом:
[> help(имя)[;\:]
[> example(имя)[;\:]
§ 2. Применение пакета Maple к решению задач математического анализа
В этом параграфе будет рассмотрено применение Maple к решению часто встречающихся задач математического анализа. В состав ядра Maple входит достаточное количество встроенных процедур и функций [1, 9, 12, 13], ориентированных на решение задач математического анализа. В табл. 2.1 приводится список процедур и функций, которые нам потребуются в дальнейшем.
Таблица 2.1.
| Процедура, функция | Назначение процедуры, функции |
| plot(f(x),x) | Построение графика функции 
|
| solve(f(x),x) | Решение уравнения  , неравенства , неравенства 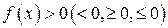
|
| fsolve(f(x),x) | Решение нелинейного уравнения  или неравенства или неравенства  
|
| diff(f(x),x[i]) | Процедура дифференцирования функции  по переменной по переменной 
|
| int(f(x),x[i]) | Процедура интегрирования функции  по переменной по переменной 
|
| int(f(x),x=a..b) | Вычисление определенного ( ) или несобственного ( ) или несобственного ( ) интеграла ) интеграла
|
| piecewise(f1,g1,…,fn,gn) | Определение кусочно-заданной функции в виде 
|
| limit(f(x),x=x0,dir) | Нахождение предела функции  в точке в точке  , dir - параметр, принимающий значения left (предел слева), right (предел , dir - параметр, принимающий значения left (предел слева), right (предел
|
Окончание табл.2.1.
| справа) | |
| discont(f(x),x) | Функция, возвращающая значения  , в которых нарушается условие непрерывности функции , в которых нарушается условие непрерывности функции 
|
| maximized(f(x), x=a..b) minimized(f(x), x=a..b) | Нахождение наибольшего и наименьшего значений функции  на отрезке на отрезке 
|
| ехtrema(f(x),{переменные}) | Нахождение безусловных экстремумов функции  нескольких переменных нескольких переменных
|
| ехtrema(f(x),{g(x)}, {переменные}) | Нахождение условных экстремумов функции  с условием с условием 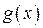
|
2.1. Дифференциальное исчисление функции одной переменной
Покажем, как применяется аппарат Maple при исследовании функции одной переменной. А график, построенный командой plot, будем использовать в качестве иллюстрации полученных результатов.
Пример 2.1. Провести полное исследование функции  . Решение
. Решение
Рабочий лист в среде Maple имеет следующий вид.
[> restart; f(x):=(3-x)*exp(x);
 /определяем точки разрыва функции и область
/определяем точки разрыва функции и область  значений функции /
[> Point_Discont:=discont(f(x),x); E_f:={limit(f(x),
x=-infinity), limit(f(x), x=+infinity)}; значений функции /
[> Point_Discont:=discont(f(x),x); E_f:={limit(f(x),
x=-infinity), limit(f(x), x=+infinity)};

 /проверяем функцию на четность
/проверяем функцию на четность  и нечетность и нечетность  с помощью команды evalb/
[> evalb(f(-x)=f(x)); evalb(f(-x)=-f(x)); с помощью команды evalb/
[> evalb(f(-x)=f(x)); evalb(f(-x)=-f(x));
  /функция является функцией общего вида/
/находим уравнение
/функция является функцией общего вида/
/находим уравнение 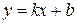 ( ( , ,  ) наклонной или горизонтальной асимптоты с помощью команды limit/
[> k[1]:=limit(f(x)/x, x=-infinity); k[2]:=limit(f(x)/x,
x=+infinity); ) наклонной или горизонтальной асимптоты с помощью команды limit/
[> k[1]:=limit(f(x)/x, x=-infinity); k[2]:=limit(f(x)/x,
x=+infinity);

 [> b[1]:=limit(f(x)-k[1]*x, x=-infinity);
b[2]:=limit(f(x)-k[2]*x, x=+infinity);
[> b[1]:=limit(f(x)-k[1]*x, x=-infinity);
b[2]:=limit(f(x)-k[2]*x, x=+infinity);
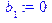
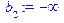 /график функции имеет горизонтальную асимптоту
/график функции имеет горизонтальную асимптоту  на на  /
/определяем области знакоположительности (OBlast_ZnakoPol_f) и знакоотрицательности (OBlast_ZnakoOtr_f) функции, а также нули функции/
[> OBlast_ZnakoPol_f:=solve(f(x)>0,x);
OBlast_ZnakoOtr_f:=solve(f(x)<0,x); Null_f:=solve(f(x)=0,x); /
/определяем области знакоположительности (OBlast_ZnakoPol_f) и знакоотрицательности (OBlast_ZnakoOtr_f) функции, а также нули функции/
[> OBlast_ZnakoPol_f:=solve(f(x)>0,x);
OBlast_ZnakoOtr_f:=solve(f(x)<0,x); Null_f:=solve(f(x)=0,x);


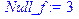 /находим первую производную
/находим первую производную  функции, стационарную точку функции функции, стационарную точку функции  , определяем интервалы возрастания (Interval_Vosrastan) и убывания (Interval_Ubyvan) функции/
[> g(x):=diff(f(x),x); x[0]:=fsolve(g(x)=0,x); , определяем интервалы возрастания (Interval_Vosrastan) и убывания (Interval_Ubyvan) функции/
[> g(x):=diff(f(x),x); x[0]:=fsolve(g(x)=0,x);
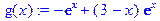
 [> Interval_Vosrastan:=solve(g(x)>0,x);
Interval_Ubyvan:=solve(g(x)<0,x);
[> Interval_Vosrastan:=solve(g(x)>0,x);
Interval_Ubyvan:=solve(g(x)<0,x);
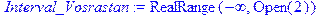
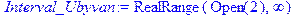 /находим вторую производную
/находим вторую производную  функции, определяем интервалы выпуклости вниз (Interval_Vypuklost_Vnis) и выпуклости вверх (Interval_Vypuklost_Vverh) функции/
[> h(x):=diff(f(x),x$2); x[1]:=fsolve(h(x)=0,x); функции, определяем интервалы выпуклости вниз (Interval_Vypuklost_Vnis) и выпуклости вверх (Interval_Vypuklost_Vverh) функции/
[> h(x):=diff(f(x),x$2); x[1]:=fsolve(h(x)=0,x);

 [> Interval_Vypuklost_Vnis:=solve(h(x)>0,x);
Interval_Vypuklost_Vverh:=solve(h(x)<0,x);
[> Interval_Vypuklost_Vnis:=solve(h(x)>0,x);
Interval_Vypuklost_Vverh:=solve(h(x)<0,x);

 /строимграфикфункции/
[> plot((3-x)*exp(x),x=-3..4, color=black, thickness=3);
/строимграфикфункции/
[> plot((3-x)*exp(x),x=-3..4, color=black, thickness=3);

|
2.2. Дифференциальное исчисление функции многих переменных
В данном разделе рассмотрим применение аппарата Maple к вычислению частных производных и нахождению экстремумов функции многих переменных. Встроенная в ядро Maple функция дифференцирования diff применима к функции  многих переменных
многих переменных  . Ее формат для вычисления частной производной
. Ее формат для вычисления частной производной 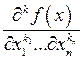 (
( ) имеет вид:
) имеет вид:
[> diff(f(x), x1$k1, …, xn$kn);
Пример 2.2. Дана функция  . Найти частные производные первого и второго порядков, проверить справедливость равенства смешанных производных второго порядка.
. Найти частные производные первого и второго порядков, проверить справедливость равенства смешанных производных второго порядка.
[> z:=cos(x*x+y)-exp(x-y*y);
/задаем функцию/
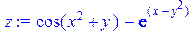 [> dzdx:=diff(z,x); dzdy:=diff(z,y);
/вычисляем частные производные первого порядка/
[> dzdx:=diff(z,x); dzdy:=diff(z,y);
/вычисляем частные производные первого порядка/
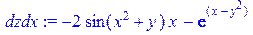
 [> d2zdx2:=diff(z,x$2); d2zdy2:=diff(z,y$2);
/вычисляем частные производные второго порядка/
[> d2zdx2:=diff(z,x$2); d2zdy2:=diff(z,y$2);
/вычисляем частные производные второго порядка/

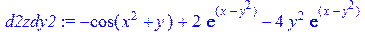 [> d2zdxdy:=diff(z,x,y); d2zdydx:=diff(z,y,x);
/вычисляем смешанные производные второго порядка/
[> d2zdxdy:=diff(z,x,y); d2zdydx:=diff(z,y,x);
/вычисляем смешанные производные второго порядка/
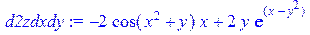
 [> evalb(d2zdxdy=d2zdydx);
/проверяем равенство смешанных производных/
[> evalb(d2zdxdy=d2zdydx);
/проверяем равенство смешанных производных/
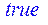
|
Безусловные экстремумы функции  переменной
переменной  находятся с помощью встроенной процедуры ехtrema:
находятся с помощью встроенной процедуры ехtrema:
[> ехtrema(f(x),{},{переменные});
Однако эта функция, как мы увидим из примера, дает только точки, подозрительные на экстремум. Для точного ответа на вопрос об экстремуме необходимо исследовать функцию с помощью известного критерия Сильвестра.
Пример 2.3. Исследовать на безусловный экстремум функцию
 .
.
Рабочий лист Maple имеет вид:
[> z:=2*x[1]^2-4*x[1]*x[2]+2*x[2]^2-x[1]^4-x[2]^4:
[> plot3d(z, x[1]=-2..2, x[2]=-2..2);
/строим график целевой функции/
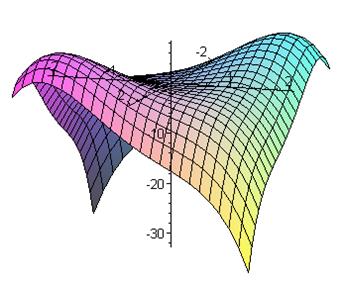 /из графика функции видно, что она имеет две точки максимума/
[> extrema(z,{},{x[1],x[2]});
/вычисляем возможные экстремумы/
/из графика функции видно, что она имеет две точки максимума/
[> extrema(z,{},{x[1],x[2]});
/вычисляем возможные экстремумы/
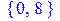 [> dzdx1:=diff(z,x[1]); dzdx2:=diff(z,x[2]);
/вычисляем частные производные первого порядка/
[> dzdx1:=diff(z,x[1]); dzdx2:=diff(z,x[2]);
/вычисляем частные производные первого порядка/
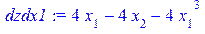
 [> fsolve({dzdx1=0,dzdx2=0},{x[1],x[2]});
/вычисляем точку возможного экстремума, пользуясь необходимым признаком точки экстремума/
[> fsolve({dzdx1=0,dzdx2=0},{x[1],x[2]});
/вычисляем точку возможного экстремума, пользуясь необходимым признаком точки экстремума/

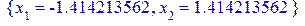
 [> d2zdx12:=diff(z,x[1]$2); d2zdx22:=diff(z,x[2]$2); d2zdx1dx2:=diff(z,x[1],x[2]);
/вычисляем частные производные второго порядка/
[> d2zdx12:=diff(z,x[1]$2); d2zdx22:=diff(z,x[2]$2); d2zdx1dx2:=diff(z,x[1],x[2]);
/вычисляем частные производные второго порядка/


 [>Gesse:= Matrix(2,2,[[d2zdx12,d2zdx1dx2],[d2zdx1dx2,d2zdx22]]); /строим матрицу Гессе частных производных второго порядка /
[>Gesse:= Matrix(2,2,[[d2zdx12,d2zdx1dx2],[d2zdx1dx2,d2zdx22]]); /строим матрицу Гессе частных производных второго порядка /
 /Ниже исследуется точка
/Ниже исследуется точка  возможного экстремума с помощью критерия Сильвестра/
[> x[1]:=1.414213562: x[2]:=-1.414213562: Gesse; Delta[1]:=
Gesse[1,1]; Delta[2]:=Gesse[1,1]*Gesse[2,2]-Gesse[1,2]^2; возможного экстремума с помощью критерия Сильвестра/
[> x[1]:=1.414213562: x[2]:=-1.414213562: Gesse; Delta[1]:=
Gesse[1,1]; Delta[2]:=Gesse[1,1]*Gesse[2,2]-Gesse[1,2]^2;

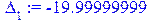 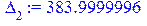
|
Согласно критерию Сильвестра точка  является точкой максимума функции. Вторая точка
является точкой максимума функции. Вторая точка  также является точкой максимума функции (матрица Гессе в ней имеет такой же вид).
также является точкой максимума функции (матрица Гессе в ней имеет такой же вид).
Исследуем точку  с помощью критерия Сильвестра.
с помощью критерия Сильвестра.
[> x[1]:=0: x[2]:=0: Gesse; Delta[1]:=Gesse[1,1];
Delta[2]:=Gesse[1,1]*Gesse[2,2]-Gesse[1,2]^2;
[> restart;z:=2*x[1]^2-4*x[1]*x[2]+2*x[2]^2-x[1]^4-x[2]^4:
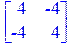  
|
Главный минор  матрицы Гессе равен нулю, следовательно, необходимо проводить дополнительные исследования. Ниже показано, что при:
матрицы Гессе равен нулю, следовательно, необходимо проводить дополнительные исследования. Ниже показано, что при:
 ,
, 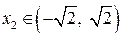 :
:  ,
,
 :
: 
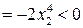 .
.
В достаточно малой окрестности точки  функция меняет свой знак (при этом
функция меняет свой знак (при этом  ), и точка
), и точка  не является точкой экстремума.
не является точкой экстремума.
[> x[1]:=0: z; solve(z>=0, x[2]);
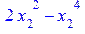
 [> x[1]:=x[2]: z; solve(z<0, x[2]);
[> x[1]:=x[2]: z; solve(z<0, x[2]);


|
Условные экстремумы функции  многих переменных
многих переменных  находятся с помощью той же процедуры ехtrema, только в фигурных скобках {} указываются ограничения (уравнения связи) на переменные
находятся с помощью той же процедуры ехtrema, только в фигурных скобках {} указываются ограничения (уравнения связи) на переменные  .
.
Известно, что задача на условный экстремум ставится так: найти точку 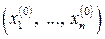 условного экстремума (максимума или минимума) функции
условного экстремума (максимума или минимума) функции  , если на переменные
, если на переменные  накладываются дополнительные ограничения (уравнения связи):
накладываются дополнительные ограничения (уравнения связи): 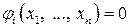 (
( ).
).
Пример 2.4. Найти точку условного экстремума функции
 ,
,
где переменные 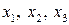 удовлетворяют уравнениям связи
удовлетворяют уравнениям связи
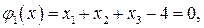

Решение
Рабочий лист Maple имеет вид:
[> z:=x[1]*x[2]*x[3]; phi[1]:=x[1]+x[2]+x[3]-4;
phi[2]:=x[1]*x[2]+x[1]*x[3]+x[2]*x[3]-5;
 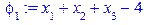  /Находим экстремумы функции с помощью команды ехtrema (заметим, что команда выдает нам только значение экстремума функции)/
[> extrema(z,{phi[1],phi[2]},{x[1],x[2],x[3]});
/Находим экстремумы функции с помощью команды ехtrema (заметим, что команда выдает нам только значение экстремума функции)/
[> extrema(z,{phi[1],phi[2]},{x[1],x[2],x[3]});
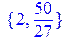 /С помощью процедуры solve находим точки возможного условного экстремума функции/
[> solve({z=2,phi[1],phi[2]},{x[1],x[2],x[3]});
/С помощью процедуры solve находим точки возможного условного экстремума функции/
[> solve({z=2,phi[1],phi[2]},{x[1],x[2],x[3]});
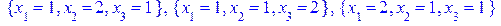 [> solve({z=50/27,phi[1],phi[2]},{x[1],x[2],x[3]});
[> solve({z=50/27,phi[1],phi[2]},{x[1],x[2],x[3]});
 /Строим функцию Лагранжа
/Строим функцию Лагранжа  . Применяя необходимый признак условного экстремума . Применяя необходимый признак условного экстремума
 для функции Лагранжа, находим ее условно-стационарные точки/
[> L:=z+lambda[1]*phi[1]+lambda[2]*phi[2];
для функции Лагранжа, находим ее условно-стационарные точки/
[> L:=z+lambda[1]*phi[1]+lambda[2]*phi[2];
 [> dLdx1:=diff(L,x[1]); dLdx2:=diff(L,x[2]);
dLdx3:=diff(L,x[3]); dLdlambda1:=diff(L,lambda[1]);
dLdlambda2:=diff(L,lambda[2]);
[> dLdx1:=diff(L,x[1]); dLdx2:=diff(L,x[2]);
dLdx3:=diff(L,x[3]); dLdlambda1:=diff(L,lambda[1]);
dLdlambda2:=diff(L,lambda[2]);




 [> Uslov_Stat_Point:=solve({dLdx1=0, dLdx2=0, dLdx3=0,
dLdlambda1=0, dLdlambda2=0},{x[1],x[2],x[3],lambda[1],
lambda[2]}):
[> Uslov_Stat_Point[1]; Uslov_Stat_Point[2];
Uslov_Stat_Point[3]; Uslov_Stat_Point[4];
Uslov_Stat_Point[5];Uslov_Stat_Point[6];
[> Uslov_Stat_Point:=solve({dLdx1=0, dLdx2=0, dLdx3=0,
dLdlambda1=0, dLdlambda2=0},{x[1],x[2],x[3],lambda[1],
lambda[2]}):
[> Uslov_Stat_Point[1]; Uslov_Stat_Point[2];
Uslov_Stat_Point[3]; Uslov_Stat_Point[4];
Uslov_Stat_Point[5];Uslov_Stat_Point[6];


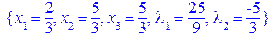
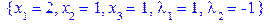


|
Далее с помощью достаточного признака условного экстремума выясняем, является ли 
 точкой условного экстремума. Для этого построим квадратичную форму второго дифференциала для функции Лагранжа в точке
точкой условного экстремума. Для этого построим квадратичную форму второго дифференциала для функции Лагранжа в точке  :
:
 ,
,
где приращения  переменных
переменных 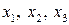 связаны соотношениями
связаны соотношениями

или в обозначениях Maple
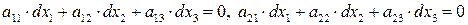
(связь между  найдем, решив соответствующую систему уравнений).
найдем, решив соответствующую систему уравнений).
[> d2Ldx1dx1:=diff(L,x[1]$2); d2Ldx2dx2:=diff(L,x[2]$2);
d2Ldx3dx3:=diff(L,x[3]$2); d2Ldx1dx2:=diff(L,x[1],x[2]);
d2Ldx1dx3:=diff(L,x[1],x[3]); d2Ldx2dx3:=diff(L,x[2],x[3]);
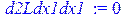




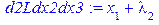 [> a[1,1]:=diff(phi[1],x[1]); a[1,2]:=diff(phi[1],x[2]);
a[1,3]:=diff(phi[1],x[3]);
[> a[1,1]:=diff(phi[1],x[1]); a[1,2]:=diff(phi[1],x[2]);
a[1,3]:=diff(phi[1],x[3]);


 [> a[2,1]:=diff(phi[2], x[1]); a[2,2]:=diff(phi[2], x[2]);
a[2,3]:=diff(phi[2], x[3]);
[> a[2,1]:=diff(phi[2], x[1]); a[2,2]:=diff(phi[2], x[2]);
a[2,3]:=diff(phi[2], x[3]);

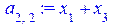
 [> eq1:=a[1,1]*dx[1]+a[1,2]*dx[2]+a[1,3]*dx[3]=0;
eq2:=a[2,1]*dx[1]+a[2,2]*dx[2]+a[2,3]*dx[3]=0;
[> eq1:=a[1,1]*dx[1]+a[1,2]*dx[2]+a[1,3]*dx[3]=0;
eq2:=a[2,1]*dx[1]+a[2,2]*dx[2]+a[2,3]*dx[3]=0;

 [> x[1]:=1: x[2]:=1: x[3]:=2: lambda[1]:=1: lambda[2]:=-1:
solve({eq1,eq2},{dx[1],dx[2],dx[3]});
[> x[1]:=1: x[2]:=1: x[3]:=2: lambda[1]:=1: lambda[2]:=-1:
solve({eq1,eq2},{dx[1],dx[2],dx[3]});
 [> Forma_Vtorogo_Porydka:=d2Ldx1dx1*dx[1]*dx[1]+
d2Ldx2dx2*dx[2]*dx[2]+d2Ldx3dx3*dx[3]*dx[3]+
2*d2Ldx1dx2*dx[1]*dx[2]+2*d2Ldx1dx3*dx[1]*dx[3]+
2*d2Ldx2dx3*dx[2]*dx[3];
[> Forma_Vtorogo_Porydka:=d2Ldx1dx1*dx[1]*dx[1]+
d2Ldx2dx2*dx[2]*dx[2]+d2Ldx3dx3*dx[3]*dx[3]+
2*d2Ldx1dx2*dx[1]*dx[2]+2*d2Ldx1dx3*dx[1]*dx[3]+
2*d2Ldx2dx3*dx[2]*dx[3];

|
Учитывая, что 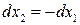 , получаем
, получаем  . Это означает, что
. Это означает, что  есть точка максимума для функции
есть точка максимума для функции  , где переменные
, где переменные 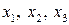 удовлетворяют двум уравнениям связи
удовлетворяют двум уравнениям связи 
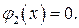
§ 3. Описание пакета LinearAlgebra
В Maple имеется пакет LinearAlgebra, ориентированный на решение задач линейной (матричной) алгебры. Он загружается соответствующей командой:
[> with(LinearAlgebra);
После выполнения этих команд система выводит на экран список процедур и функций, которыми располагает пакет LinearAlgebra.
Пакет LinearAlgebra является более мощным и совершенным по сравнению с linalg (в ранних версиях программы). Он предназначен для работы с матрицами и векторами больших размеров. Самым простым образом матрицу  размером
размером  в пакете LinearAlgebra можно сформировать при помощи команды
в пакете LinearAlgebra можно сформировать при помощи команды
[> Matrix(m, n, [[a[1,1],…,a[1,n]],…,[a[m,1],…,a[m,n]]]);
Приведем в табл. 3.1 назначение наиболее часто применимых процедур и функций пакета LinearAlgebra. Более полную информацию о каждой процедуре или функции можно узнать в справке, или набрав команду
[> help(имя_процедуры);
Таблица 3.1.
| Название процедуры, функции | Назначение процедуры, функции |
| Basis | Определяет базис для векторного пространства, заданного системой векторов |
| CharacteristicMatrix | Создает для квадратной матрицы ее характеристическую матрицу |
| CharacteristicPolynomial | Создает для квадратной матрицы ее характеристический многочлен |
| Determinant | Вычисляет для квадратной матрицы ее определитель |
| DiagonalMatrix | Создает диагональную матрицу |
| Eigenvalues | Вычисляет для квадратной матрицы ее собственные значения (собственные числа) |
| Eigenvectors | Вычисляет для квадратной матрицы ее собственные векторы (рекомендуется использовать вместе с процедурой Eigenvalues) |
| LinearSolve | Решает систему линейных алгебраических уравнений (СЛАУ) в матричной форме |
| MatrixAdd | Процедура сложения двух матриц |
| Matrixlnverse | Процедура нахождения обратной матрицы |
| MatrixMatrixMultiply | Процедура произведения двух матриц |
| MatrixNorm | Функция вычисления нормы матрицы |
| MatrixScalarMultiply | Процедура умножения матрицы на скаляр |
| MatrixVectorMultiply | Процедура умножения матрицы на вектор |
| Minor | Вычисляет минор матрицы |
| Normalize | Нормализует вектор |
| NullSpace | Возвращает нуль-пространство (ядро) матрицы |
| Rank | Вычисляет ранг матрицы |
| SylvesterMatrix | Конструирует матрицу Сильвестра из многочленов |
| Transpose | Вычисляет матрицу, транспонированную к данной |
Приведем примеры решения наиболее часто встречающихся задач линейной алгебры (исследование систем линейных алгебраических уравнений на совместность, вычисление собственных векторов и чисел матриц).
Пример 3.1. Исследовать СЛАУ с параметром  (СЛАУ задана своей расширенной матрицей) и решить в каждом случае:
(СЛАУ задана своей расширенной матрицей) и решить в каждом случае:
 .
.
Ниже приведен текст рабочего листа по решению данной задачи (с описаниями по ходу выполнения команд).
[> restart; with(LinearAlgebra):
/задаем вектор-столбцы основной матрицы/
[> a1:=Vector([2,1,3]); a2:=Vector([lambda+1,lambda,-3]);
a3:=Vector([lambda-2,-3,-7]);
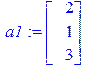

 /задаем основную матрицу и вектор-столбец свободных коэффициентов системы/
[> A:=Matrix(3,3,[a1,a2,a3]); B:=Vector([3,lambda+2,3]);
/задаем основную матрицу и вектор-столбец свободных коэффициентов системы/
[> A:=Matrix(3,3,[a1,a2,a3]); B:=Vector([3,lambda+2,3]);

 /выводим определитель основной матрицы системы, решение системы в матричном виде (при значениях, в которых определитель основной матрицы не равен нулю)/
[> Delta:=Determinant(A); X:=LinearSolve(A,B);
/выводим определитель основной матрицы системы, решение системы в матричном виде (при значениях, в которых определитель основной матрицы не равен нулю)/
[> Delta:=Determinant(A); X:=LinearSolve(A,B);

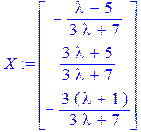 /вычисляем значения параметра
/вычисляем значения параметра  , при котором определитель обращается в нуль/
[> Korni:=solve(Determinant(A)=0); , при котором определитель обращается в нуль/
[> Korni:=solve(Determinant(A)=0);
 [> lambda:=Korni[1]; X:=LinearSolve(A,B);
[> lambda:=Korni[1]; X:=LinearSolve(A,B);
 Error,(in LinearAlgebra:-LA_Main:-LinearSolve) inconsistent system
/Maple предупреждает, что СЛАУ при данном значении параметра
Error,(in LinearAlgebra:-LA_Main:-LinearSolve) inconsistent system
/Maple предупреждает, что СЛАУ при данном значении параметра  несовместна/
[> lambda:=Korni[2]; X:=LinearSolve(A,B);
/СЛАУ имеет бесконечное множество решений при этом значении параметра несовместна/
[> lambda:=Korni[2]; X:=LinearSolve(A,B);
/СЛАУ имеет бесконечное множество решений при этом значении параметра  / /


|
Пример 3.2. Найти собственные числа и соответственные собственные векторы матрицы
 .
.
Текст рабочего листа по решению задачи имеет вид:
[> restart; with(LinearAlgebra):
[> A:=Matrix(3,3,[[3,-6,9],[1,-2,3],[-3,6,-9]]);
/задание исходной матрицы/
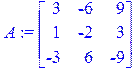 [> Add(A,-lambda): p(lambda):=Determinant(Add(A,-lambda));
/составление характеристического многочлена
[> Add(A,-lambda): p(lambda):=Determinant(Add(A,-lambda));
/составление характеристического многочлена 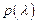 матрицы/ матрицы/
 [> solve(p(lambda)=0,{lambda});
/вычисление собственных чисел матрицы/
[> solve(p(lambda)=0,{lambda});
/вычисление собственных чисел матрицы/
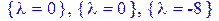 [> v:=Eigenvalues(A); F:=Eigenvectors(A);
/вычисление собственных чисел и собственных векторов матрицы с помощью процедуры Eigenvectors: первый столбец v – собственные числа матрицы, вторая матрица F содержит соответствующие собственные векторы матрицы, они расположены по столбцам!)/
[> v:=Eigenvalues(A); F:=Eigenvectors(A);
/вычисление собственных чисел и собственных векторов матрицы с помощью процедуры Eigenvectors: первый столбец v – собственные числа матрицы, вторая матрица F содержит соответствующие собственные векторы матрицы, они расположены по столбцам!)/


|
§ 4. Описание пакета Optimization
Пакет Optimization, входящий в состав Maple, предназначен для решения оптимизационных задач. Он загружается в память с помощью команды
[> with(Optimization);

Как видно, в состав этого пакета входят 8 процедур и функций. Описание наиболее важных из них приведено в табл. 4.1.
Таблица 4.1.
| Название процедуры, функции | Назначение процедуры, функции |
| Interactive | Решение оптимизационной задачи с выводом процесса решения в интерактивном виде |
| LPSolve | Решение задачи линейного программирования. Процедура равносильна решению задачи с использованием пакета simplex(см. §5) |
| Maximize | Процедура вычисления максимума целевой функции |
| Minimize | Процедура вычисления минимума целевой функции |
| NLPSolve | Решение задачи нелинейного программирования |
| QPSolve | Решение задачи квадратичного программирования |
Пусть даны целевая функция  переменной
переменной  (
(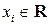 – управляющие переменные,
– управляющие переменные, 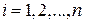 ) и система из
) и система из  ограничений, выраженных неравенствами (равенствами)
ограничений, выраженных неравенствами (равенствами)
 (4.1)
(4.1)
Ниже приведены варианты использования процедуры Maximize при решении различных оптимизационных задач:
[> Maximize(object_function);
процедура нахождения наибольшего значения целевой функции  при любых значениях управляющих переменных (решается задача на безусловный экстремум:
при любых значениях управляющих переменных (решается задача на безусловный экстремум: 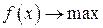 ,
, 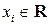 );
);
[> Maximize(object_function, { constr});
процедура нахождения наибольшего значения целевой функции  при выполнении системы ограничений {constr} (решается задача на условный экстремум:
при выполнении системы ограничений {constr} (решается задача на условный экстремум: 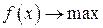 ,
, 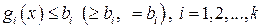 ,
, 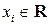 );
);
[> Maximize(object_function, { constr}, assume=nonnegative);
процедура нахождения наибольшего значения целевой функции  при выполнении системы ограничений {constr} (решается задача на условный экстремум:
при выполнении системы ограничений {constr} (решается задача на условный экстремум: 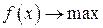 ,
, 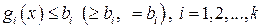 ,
, 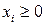 ).
).
Здесь object_function – целевая функция  , {constr} – список ограничений вида (4.1), параметр assume=nonnegative означает, что задача решается в области неотрицательных значений управляющих переменных.
, {constr} – список ограничений вида (4.1), параметр assume=nonnegative означает, что задача решается в области неотрицательных значений управляющих переменных.
Процедура NLPSolve во многих случаях описывается одним из следующих способов:
[> NLPSolve(object_function, initialpoint={x[1]=a1, x[2]=a2,
…, x[n]=an}, maximize );
решается задача нелинейного программирования на максимум целевой функции