Для каждого из заданий 1-7 необходимо составить программу в среде
Maple согласно своему номеру варианта.
Задание 1. Матричные балансовые модели макроэкономики
Задана матрица  (
( ) коэффициентов прямых затрат (технологическая матрица) и вектор
) коэффициентов прямых затрат (технологическая матрица) и вектор  валового выпуска. Требуется:
валового выпуска. Требуется:
1) Составить статическую модель Леонтьева межотраслевого баланса, найти вектор  конечного потребления;
конечного потребления;
2) доказать, что матрица  является продуктивной и найти ее запас продуктивности
является продуктивной и найти ее запас продуктивности  .
.
3) найти объем валового выпуска – вектор  , если вектор конечного потребления увеличить на вектор
, если вектор конечного потребления увеличить на вектор  .
.
Таблица 1.
| № | Матрица | № | Матрица | № | Матрица |

| 
| 
| |||

| 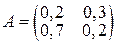
| 
| |||
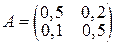
| 
| 
| |||
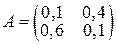
| 
| 
| |||

| 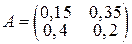
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
Задание 2. Матричные балансовые модели макроэкономики
Табл. 2 содержит данные баланса трех отраслей промышленности за некоторый период времени (фактические значения параметров  даны в табл. 3). Требуется:
даны в табл. 3). Требуется:
1) составить матрицу  (
( ) коэффициентов прямых затрат (технологическую матрицу), выяснить, является ли эта матрица продуктивной.
) коэффициентов прямых затрат (технологическую матрицу), выяснить, является ли эта матрица продуктивной.
2) Найти объем валового выпуска – вектор  :
:

каждого вида продукции, если конечное потребление (вектор  ) по отраслям увеличить соответственно на 50, 40, 30 у.е (
) по отраслям увеличить соответственно на 50, 40, 30 у.е ( ). Соответствующую СЛАУ решить двумя способами (по формулам Крамера и методом обратной матрицы). Сравнить полученные результаты.
). Соответствующую СЛАУ решить двумя способами (по формулам Крамера и методом обратной матрицы). Сравнить полученные результаты.
3) Найти для матрицы  ее запас продуктивности
ее запас продуктивности  .
.
4) Считая статическую модель Леонтьева межотраслевого баланса прямой задачей, составить для нее двойственную задачу и решить ее.
5) Структуру конечного спроса задать в виде (см. табл. 2)
 .
.
Производственные ресурсы ограничены величиной  у.е. Используя технологическую матрицу
у.е. Используя технологическую матрицу  из пункта 1, найти вектор
из пункта 1, найти вектор  валового выпуска, вектор
валового выпуска, вектор  двойственных оценок материальных ресурсов и ставку
двойственных оценок материальных ресурсов и ставку  зарплаты. Проверить справедливость равенства
зарплаты. Проверить справедливость равенства
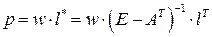 ,
,  .
.
Таблица 2.
| № | Отрасль | Производств.
потребление 
| Конечный продукт 
| Валовой
выпуск 
| ||
| Добыча и переработка | 
| 
| 
| 
| 
| |
| Энергетика | 
| 
| 
| 
| 
| |
| Машиностроение | 
| 
| 
| 
| 
|
Таблица 3.
| № вар. | 
| 
| 
| 
| № вар. | 
| 
| 
| 
|
Линейная модель международной торговли
Линейная модель международной торговли была предложена Д. Риккардо в XVIII веке. Будем предполагать, что 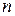 стран ведут торговлю. Обозначим через
стран ведут торговлю. Обозначим через  части национальных бюджетов этих стран, которые расходуются на покупку товаров. Эти величины называются национальными торговыми бюджетами.
части национальных бюджетов этих стран, которые расходуются на покупку товаров. Эти величины называются национальными торговыми бюджетами.
Пусть 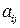 – доля бюджета
– доля бюджета  , которую
, которую  -я страна тратит на закупку товаров у
-я страна тратит на закупку товаров у  -ой страны. Введем матрицу коэффициентов
-ой страны. Введем матрицу коэффициентов 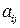
 .
.
Так как национальный торговый бюджет расходуется только на закупки товаров внутри страны и вне ее, то справедливы равенства
 .
.
Матрицу  с приведенным выше свойством называют структурной матрицей торговли.
с приведенным выше свойством называют структурной матрицей торговли.
Можно показать [3], что условие сбалансированной (бездефицитной) торговли заключается в выполнении равенств
 ,
,  .
.
Введя в рассмотрение вектор-столбец национальных торговых бюджетов  , условие сбалансированной (бездефицитной) торговли можно записать в матричной форме
, условие сбалансированной (бездефицитной) торговли можно записать в матричной форме
 .
.
Это уравнение означает, что собственный вектор структурной матрицы торговли 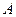 , соответствующий ее собственному значению
, соответствующий ее собственному значению 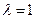 , состоит из национальных торговых бюджетов стран, удовлетворяющих условию бездефицитной международной торговли.
, состоит из национальных торговых бюджетов стран, удовлетворяющих условию бездефицитной международной торговли.
Задание 3. Линейная модель международной торговли
Задана матрица  структурной торговли (табл. 4). Требуется:
структурной торговли (табл. 4). Требуется:
1) Пользуясь теоремой о цепочке, составить какую-нибудь замкнутую цепочку импорта;
2) найти национальные доходы торгующих стран в сбалансированной системе международной торговли.
Таблица 4.
| № | Матрица | № | Матрица |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 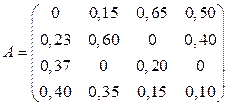
| ||
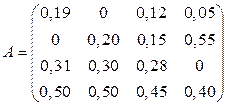
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 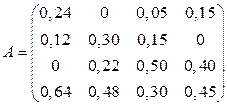
| ||
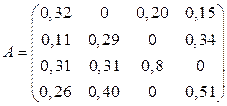
| 
| ||

| 
| ||

| 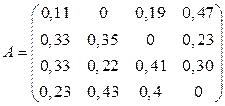
|
Задание 4. Моделирование поведения потребителя
Дана функция полезности  от двух видов товаров (табл. 5). Цены на товары равны соответственно
от двух видов товаров (табл. 5). Цены на товары равны соответственно  и
и  д.е., доход потребителя ограничен величиной
д.е., доход потребителя ограничен величиной  д.е. Найти:
д.е. Найти:
1) оптимальное распределение товаров  и
и 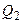 (точку локального рыночного равновесия);
(точку локального рыночного равновесия);
2) получить общий вид функций потребительского спроса, а также:
а) прямые функции спроса  ,
,  в зависимости от цен;
в зависимости от цен;
б) перекрестные функции спроса  ,
,  в зависимости от цен;
в зависимости от цен;
в) функции спроса  ,
,  в зависимости от дохода потребителя. Выяснить к какому типу принадлежат товары
в зависимости от дохода потребителя. Выяснить к какому типу принадлежат товары 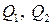 .
.
3) Найти частичные коэффициенты эластичности функций спроса, полученных при решении задачи потребительского выбора.
4) Рассчитать по уравнению Слуцкого эффекты замены при наличии компенсации для товаров 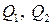 . Оценить товары
. Оценить товары 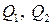 с точки зрения их взаимозаменяемости или взаимодополняемости.
с точки зрения их взаимозаменяемости или взаимодополняемости.
Таблица 5.
| № вар. | Функция полезности 
| Цена

| Цена

| Величина дохода 
|
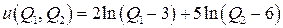 Логарифмическая Ф2П
Логарифмическая Ф2П
| ||||
 Функция Торнквиста двух переменных
Функция Торнквиста двух переменных
| ||||
 Мультипликативная Ф2П Стоуна
Мультипликативная Ф2П Стоуна
| ||||
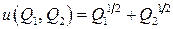 Аддитивная Ф2П
Аддитивная Ф2П
| ||||

| ||||

| ||||
 Логарифмическая Ф2П
Логарифмическая Ф2П
| ||||
 Функция Торнквиста двух переменных
Функция Торнквиста двух переменных
| 0,05 | 0,3 | ||
 Мультипликативная Ф2П Стоуна
Мультипликативная Ф2П Стоуна
| ||||
 Аддитивная Ф2П
Аддитивная Ф2П
| ||||

| ||||

| 1,3 | 2,1 | ||
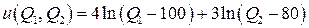 Логарифмическая Ф2П
Логарифмическая Ф2П
| 0,2 | 0,3 | ||
 Функция Торнквиста двух переменных
Функция Торнквиста двух переменных
| 0.1 | 0.6 | ||
 Мультипликативная Ф2П Стоуна
Мультипликативная Ф2П Стоуна
| ||||
 Аддитивная Ф2П
Аддитивная Ф2П
| ||||
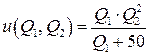
| ||||

| 0,3 | 0,15 | ||
 Логарифмическая Ф2П
Логарифмическая Ф2П
| 2,4 | 3,3 | ||
 Функция Торнквиста двух переменных
Функция Торнквиста двух переменных
| ||||
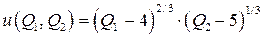 Мультипликативная Ф2П Стоуна
Мультипликативная Ф2П Стоуна
| ||||
 Аддитивная Ф2П
Аддитивная Ф2П
| 0,01 | 0,02 | ||

| ||||

| 1,3 | 2,1 | ||
 Логарифмическая Ф2П
Логарифмическая Ф2П
| 0.01 | 0.02 | ||
 Функция Торнквиста двух переменных
Функция Торнквиста двух переменных
| 1,9 | 2,4 | ||
 Мультипликативная Ф2П Стоуна
Мультипликативная Ф2П Стоуна
| ||||
 Аддитивная Ф2П
Аддитивная Ф2П
| 0,05 | 0,1 | ||
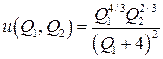
| 0,5 | 0,8 | ||

| 5,1 |
Задание 5. Построение функции спроса с помощью коэффициента эластичности. Логистические кривые
В табл. 6 даны формулы, определяющие коэффициент эластичности 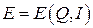 . Требуется найти аналитический вид функции спроса
. Требуется найти аналитический вид функции спроса 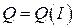 на товар в зависимости от дохода
на товар в зависимости от дохода  , построить соответствующую логистическую кривую.
, построить соответствующую логистическую кривую.
Таблица 6.
| № | Коэффициент эластичности
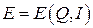
| Начальное
условие 
|

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 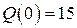
| |

| 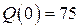
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 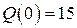
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
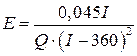
| 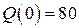
| |

| 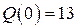
| |
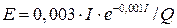
| 
| |

| 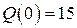
| |

| 
| |

| 
| |

| 
|
Задание 6. Моделирование поведения производителя
1) Дана производственная функция (ПФ)  (см. табл. 7). Выяснить, является ли она неоклассической. Найти основные характеристики этой функции, построить соответствующую поверхность, найти уравнения изоквант и построить карту изоквант;
(см. табл. 7). Выяснить, является ли она неоклассической. Найти основные характеристики этой функции, построить соответствующую поверхность, найти уравнения изоквант и построить карту изоквант;
2) Пусть цена единицы продукции  денежных единиц (д.е.), функция издержек линейна, стоимость аренды единицы производственных фондов
денежных единиц (д.е.), функция издержек линейна, стоимость аренды единицы производственных фондов 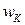 д.е., ставка заработной платы
д.е., ставка заработной платы  д.е. на человека. Найти функции спроса на ресурсы
д.е. на человека. Найти функции спроса на ресурсы
 ,
,
функцию предложения выпуска
 ,
,
оптимальное распределение ресурсов  и соответствующую ему прибыль от производства в долгосрочном периоде и в краткосрочном периоде (в последнем случае затраты ресурсов ограничены величиной
и соответствующую ему прибыль от производства в долгосрочном периоде и в краткосрочном периоде (в последнем случае затраты ресурсов ограничены величиной  д.е.). Вычислить рыночную цену
д.е.). Вычислить рыночную цену  единицы продукции;
единицы продукции;
3) зная в явном виде функции спроса на ресурсы и функцию предложения, оценить поведения производителя на изменения цен на ресурсы и цены продукции;
4) найти точку  наиболее экономичного производства, что при уровне выпуска
наиболее экономичного производства, что при уровне выпуска  издержки
издержки  минимальны.
минимальны.
Таблица 7.
| № | 
| 
| 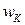
| 
| 
|

| |||||

| |||||

| |||||

| |||||

| 0,2 | 0,02 | 0,03 | ||

| |||||

| |||||

| 0,3 | 0,6 | |||

| 2,5 | ||||

| 0,09 | 0,04 | 0,02 | ||

| |||||
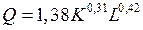
| 0,12 | 0,01 | 0,03 | ||

| 0,2 | 0,3 | |||

| 0,1 | 0,01 | 0,02 | ||
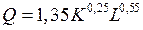
| 1,5 | 2,5 | |||

| 0,5 | 0,4 | |||

| 3,5 | 2,2 | 2,1 | ||

| 1,15 | 0,9 | 0,5 | ||

| 0,2 | 0,35 | |||

| |||||

| 3,2 | 1,2 | 1,5 | ||

| 1,2 | 2,3 | |||

| 0,08 | 0,02 | 0,04 | ||

| 4,5 | ||||

| 3,2 | 1,1 | 1,4 | ||

| 8,7 | 6,5 | 3,2 | ||

| 0,2 | 0,001 | 0,002 | ||

| 0,5 | 0,4 | |||

| 2,1 | 1,6 | 1,3 | ||

| 4,5 | 2,2 | 1,5 |
Задание 7. Моделирование рыночного равновесия
Даны логистическая функция спроса  и функции предложения
и функции предложения 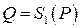 ,
,  (табл. 8).
(табл. 8).
1) Найти равновесную цену  для модели «спрос-предложение»
для модели «спрос-предложение»  , исследовать на сходимость и построить последовательность цен
, исследовать на сходимость и построить последовательность цен  , пользуясь моделью с запаздыванием спроса (модель А);
, пользуясь моделью с запаздыванием спроса (модель А);
2)Найти равновесную цену  для модели «спрос-предложение»
для модели «спрос-предложение»
 , исследовать на сходимость и построить последовательность цен
, исследовать на сходимость и построить последовательность цен  , пользуясь моделью с запаздыванием предложения (модель В).
, пользуясь моделью с запаздыванием предложения (модель В).
Таблица 8.
| № | 
| 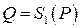
| 
|

| 
| 
| |

| 
| 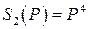
| |

| 
| 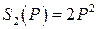
| |

| 
| 
| |

| 
| 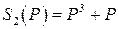
| |

| 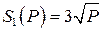
| 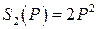
| |

| 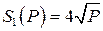
| 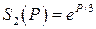
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 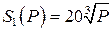
| 
| |
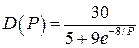
| 
| 
| |

| 
| 
| |
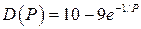
| 
| 
| |

| 
| 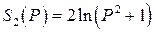
| |

| 
| 
| |

| 
| 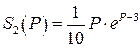
| |

| 
| 
| |
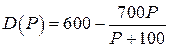
| 
| 
| |

| 
| 
| |

| 
| 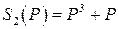
| |

| 
| 
| |
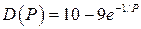
| 
| 
| |
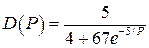
| 
| 
| |

| 
| 
| |
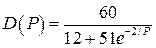
| 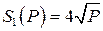
| 
| |

| 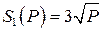
| 
| |

| 
| 
| |

| 
| 
|
Библиографический список
1. Дьяконов В.П. Математическая система Maple: учебный курс. – СПб.: Питер, 2001. – 608 с.
2. Замков О.О. Математические методы в экономике: учебник / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. – М.: Дело и сервис, 1998.
3. Колемаев В.А. Математическая экономика / В.А. Колемаев. – М.: ЮНИТИ-