Задача поиска равновесной цены  представляет собой торг между производителем и покупателем. В процессе торга возникает последовательность
представляет собой торг между производителем и покупателем. В процессе торга возникает последовательность  , состоящая из называемых производителем и покупателем цен. В зависимости от используемых гипотез в дискретной модели динамики цен происходит либо запаздывание спроса (назовем ее модель А), либо запаздывание предложения (назовем ее модель В).
, состоящая из называемых производителем и покупателем цен. В зависимости от используемых гипотез в дискретной модели динамики цен происходит либо запаздывание спроса (назовем ее модель А), либо запаздывание предложения (назовем ее модель В).
В табл. 9.1 представлены сравнительные характеристики этих моделей.
Таблица 9.1.
| Характеристики | Модель с запаздыванием спроса (модель А) | Модель с запаздыванием предложения (модель В) |
| Модель предложения | Предложение определяется по уровню цен предыдущего периода (товаропроизводитель прогнозирует цену следующего периода) | Предложение определяется по уровню спроса предыдущего периода (товаропроизводитель ориентируется на спрос за предыдущий период) |
| Модель потребления | Потребляется все, что предлагается | Потребление 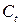 не превосходит ни предложение, ни спрос: не превосходит ни предложение, ни спрос:
 . .
|
| Модель ценообразования | Цена задается из условия равновесия в соответствии с функцией спроса | Цена устанавливается из условия равновесия в соответствии с функцией предложения |
| Вид (формула) итерационного процесса |  , ,

|  , ,

|
Продолжение таблицы 9.1.
| Алгоритм “нащупывания” равновесной цены | 1. Товаропроизводитель по значению цены  с помощью кривой потребления определяет с помощью кривой потребления определяет 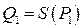 .
2. В силу модели ценообразования на рынке устанавливается цена .
2. В силу модели ценообразования на рынке устанавливается цена  в соответствии с кривой спроса, причем в соответствии с кривой спроса, причем  есть решение уравнения есть решение уравнения  .
3. Товаропроизводитель, ориентируясь на цену .
3. Товаропроизводитель, ориентируясь на цену  , определяет объем предложения , определяет объем предложения  .
4. Рассмотренный процесс повторяется. Получаем последовательность цен .
4. Рассмотренный процесс повторяется. Получаем последовательность цен  . .
| 1. На первом шаге при цене  имеет место избыточный спрос: имеет место избыточный спрос:  .
Потребление равно предложению: .
Потребление равно предложению:  . Товаропроизводитель теряет часть прибыли (цена занижена, предложено товара меньше, чем могло быть продано).
2. На втором шаге товаропроизводитель устанавливает цену . Товаропроизводитель теряет часть прибыли (цена занижена, предложено товара меньше, чем могло быть продано).
2. На втором шаге товаропроизводитель устанавливает цену  , используя кривую потребления , используя кривую потребления  ( ( – решение уравнения – решение уравнения  ).
3. Цене ).
3. Цене  соответствует спрос соответствует спрос  . Потребление равно спросу: . Потребление равно спросу:
 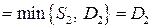 (часть предложенного товара не находит покупателя из-за высокой цены, товаропроизводитель теряет часть прибыли).
4. На третьем шаге для сохранения предложения цена снижается до уровня
(часть предложенного товара не находит покупателя из-за высокой цены, товаропроизводитель теряет часть прибыли).
4. На третьем шаге для сохранения предложения цена снижается до уровня  (решение уравнения (решение уравнения  , определяется по кривой потребления , определяется по кривой потребления  ).
5. Рассмотренный процесс повторяется. Получаем последовательность цен ).
5. Рассмотренный процесс повторяется. Получаем последовательность цен  . .
|
Условие сходимости итерационного процесса к 
|  ,
равновесная цена
устойчива ,
равновесная цена
устойчива
|  ,
равновесная цена
устойчива ,
равновесная цена
устойчива
|
| Условие расходимости итерационного процесса |  ,
равновесная цена
неустойчива ,
равновесная цена
неустойчива
|  ,
равновесная цена
неустойчива ,
равновесная цена
неустойчива
|
Окончание таблицы 9.1.
| Статическая модель Эванса | 
|
сходится при 
| сходится при 
|
На плоскости  (см. рис. 9.2) соответствующий процесс поиска равновесной цены модели А изображается в виде «паутины», которая «намотана» на кривые спроса и предложения. Это дало основание для названия модели – паутинная модель. (см. рис. 9.2) соответствующий процесс поиска равновесной цены модели А изображается в виде «паутины», которая «намотана» на кривые спроса и предложения. Это дало основание для названия модели – паутинная модель.
|  Рис. 9.2.
Рис. 9.2.
|
Пример 9.1. Даны логистическая функция спроса

и функции предложения
 ,
,  .
.
1. Найти равновесную цену  для модели «спрос-предложение»
для модели «спрос-предложение»  , исследовать на сходимость и построить последовательность цен
, исследовать на сходимость и построить последовательность цен  , пользуясь моделью с запаздыванием спроса (модель А).
, пользуясь моделью с запаздыванием спроса (модель А).
2.Найти равновесную цену  для модели «спрос-предложение»
для модели «спрос-предложение»
 , исследовать на сходимость и построить последовательность цен
, исследовать на сходимость и построить последовательность цен  , пользуясь моделью с запаздыванием предложения (модель В).
, пользуясь моделью с запаздыванием предложения (модель В).
Решение. В программе на Maple используем следующие переменные.
| Переменная | Назначение, описание |
| Function_D | Исходная функция спроса 
|
| Function_S[1] | Исходная функция предложения 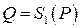
|
| Function_S[2] | Исходная функция предложения 
|
| Elast_D, Elast_S | Эластичности функций спроса и предложения по цене |
| P_Ravnoves | Значение равновесной цены 
|
| P[t] | последовательность цен  , являющихся решениями уравнений , являющихся решениями уравнений  и и 
|
| Q[t] | Значения функции предложения 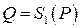 и функции спроса и функции спроса  при значении цены при значении цены 
|
| Points_P | Массив точек (цен) |
| Points_Q | Массив точек (объемов предложений) |
В программе используется структура цикла for с предопределенным количеством шагов N. Блок-схема этого цикла для решения задачи пункта 1 (схема реализует процесс “нащупывания” равновесной цены  в случае модели А) изображена на рис.9.3.
На выходе из цикла мы имеем последовательность цен в случае модели А) изображена на рис.9.3.
На выходе из цикла мы имеем последовательность цен  и соответствующих значений функции предложения и соответствующих значений функции предложения 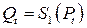 .
Подобную блок-схему можно составить и для реализации процесса “нащупывания” равновесной цены .
Подобную блок-схему можно составить и для реализации процесса “нащупывания” равновесной цены  в случае модели В. в случае модели В.
|  Рис. 9.3.
Рис. 9.3.
|
Текст программы по решению пункта 1 в среде Maple имеет вид:
[> restart; Digits:=5:
[> Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)): a[1]:=200:
a[2]:=3: a[3]:=5: a[4]:=2: Function_D:=Function_D;
Function_S[1]:=3*sqrt(P)+30: Function_S[1]:=Function_S[1];
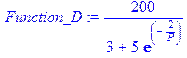
 /строим графики функций спроса и предложения, точка их пересечения – точка равновесной цены/
[> plot([Function_D, Function_S[1]], P=0..30, thickness=4, color=black);
/строим графики функций спроса и предложения, точка их пересечения – точка равновесной цены/
[> plot([Function_D, Function_S[1]], P=0..30, thickness=4, color=black);
 /вычисляем эластичности функций спроса и предложения при равновесной цене, коэффициент k. При
/вычисляем эластичности функций спроса и предложения при равновесной цене, коэффициент k. При  равновесная цена устойчива, итерационный процесс сходится/
[> Elast_D:=diff(Function_D,P)/(Function_D/P);
Elast_S:=diff(Function_S[1],P)/(Function_S[1]/P); равновесная цена устойчива, итерационный процесс сходится/
[> Elast_D:=diff(Function_D,P)/(Function_D/P);
Elast_S:=diff(Function_S[1],P)/(Function_S[1]/P);

 [> P_Ravnoves:=fsolve(Function_D=Function_S[1], P=0..infinity);
P:=P_Ravnoves: Q_Ravnoves:=Function_D;
[> P_Ravnoves:=fsolve(Function_D=Function_S[1], P=0..infinity);
P:=P_Ravnoves: Q_Ravnoves:=Function_D;

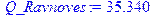 [> Elast_D:=simplify(Elast_D); Elast_S:=simplify(Elast_S);
k:=abs(Elast_S/Elast_D);
[> Elast_D:=simplify(Elast_D); Elast_S:=simplify(Elast_S);
k:=abs(Elast_S/Elast_D);


 [> P:='P': Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)):
Function_S[1]:=3*sqrt(P)+30:
/составляем цикл по нахождению последовательности
[> P:='P': Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)):
Function_S[1]:=3*sqrt(P)+30:
/составляем цикл по нахождению последовательности  цен/
[> N:=40:
[> P[1]:=P_Ravnoves-1: P:=P[1]: Q[1]:=Function_S[1]:
Point_P[1]:=P_Ravnoves-1: Point_Q[1]:=Q[1]:
for t from 2 by 1 to N do
P:='P':
P[t]:=fsolve(Function_D=Q[t-1]);
Point_P[t]:=P[t];
P:=P[t];
Q[t]:=Function_S[1];
Point_Q[t]:=Q[t];
end do:
[> t:='t': Points_P:=[[t, Point_P[t]] $t=1..N]; цен/
[> N:=40:
[> P[1]:=P_Ravnoves-1: P:=P[1]: Q[1]:=Function_S[1]:
Point_P[1]:=P_Ravnoves-1: Point_Q[1]:=Q[1]:
for t from 2 by 1 to N do
P:='P':
P[t]:=fsolve(Function_D=Q[t-1]);
Point_P[t]:=P[t];
P:=P[t];
Q[t]:=Function_S[1];
Point_Q[t]:=Q[t];
end do:
[> t:='t': Points_P:=[[t, Point_P[t]] $t=1..N];

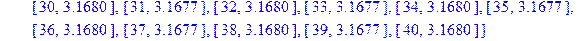 [> Points_Q:=[[t, Point_Q[t]] $t=1..N];
[> Points_Q:=[[t, Point_Q[t]] $t=1..N];

 /выводим результаты вычислений/
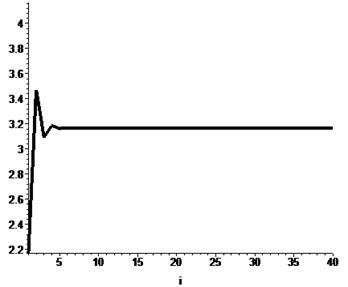
[> plot(Points_P, i=1..N, style=line, thickness=4, color=black,
view=[1..N, P_Ravnoves-1..P_Ravnoves+1]);
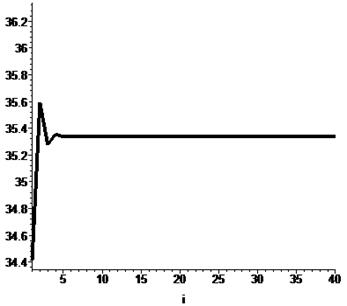
plot(Points_Q, i=1..N, style=line, thickness=4, color=black,
view=[1..N, Q_Ravnoves-1..Q_Ravnoves+1]);
/выводим результаты вычислений/
[> plot(Points_P, i=1..N, style=line, thickness=4, color=black,
view=[1..N, P_Ravnoves-1..P_Ravnoves+1]);
plot(Points_Q, i=1..N, style=line, thickness=4, color=black,
view=[1..N, Q_Ravnoves-1..Q_Ravnoves+1]);
|
Текст программы по решению пункта 2 в среде Maple имеет вид:
[> P:='P': Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)):
Function_D:=Function_D; Function_S[2]:=P*P+30:
Function_S[2]:=Function_S[2];
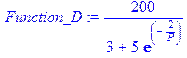
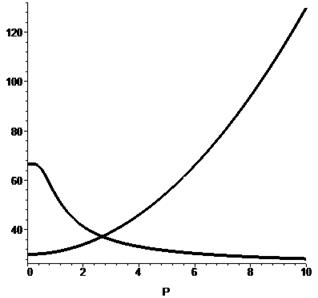
 [> plot([Function_D, Function_S[2]], P=0..10, thickness=4,
color=black);
[> plot([Function_D, Function_S[2]], P=0..10, thickness=4,
color=black);
 [> Elast_D:=diff(Function_D,P)/(Function_D/P);
Elast_S:=diff(Function_S[2],P)/(Function_S[2]/P);
[> Elast_D:=diff(Function_D,P)/(Function_D/P);
Elast_S:=diff(Function_S[2],P)/(Function_S[2]/P);

 [> P_Ravnoves:=fsolve(Function_D=Function_S[2], P=0..infinity);
P:=P_Ravnoves: Q_Ravnoves:=Function_D;
Q_Ravnoves:=Function_S[2];
[> P_Ravnoves:=fsolve(Function_D=Function_S[2], P=0..infinity);
P:=P_Ravnoves: Q_Ravnoves:=Function_D;
Q_Ravnoves:=Function_S[2];

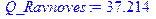
 [> Elast_D:=simplify(Elast_D); Elast_S:=simplify(Elast_S);
k:=abs(Elast_S/Elast_D);
[> Elast_D:=simplify(Elast_D); Elast_S:=simplify(Elast_S);
k:=abs(Elast_S/Elast_D);


 [> P:='P': Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)):
Function_S[2]:=P*P+30:
[> P[1]:=P_Ravnoves+1: P:=P[1]: Q[1]:=evalf(Function_D):
Point_P[1]:=P_Ravnoves+1:
for t from 2 by 1 to N do
P:='P':
P[t]:=fsolve(Function_S[2]=Q[t-1], P=0..infinity);
Point[t]:=P[t];
P:=P[t];
Q[t]:=Function_D;
Point_Q[t]:=Q[t];
end do:
[> t:='t': Points_P:=[[t, Point_P[t]] $t=1..N];
Points_Q:=[[t, Point_Q[t]] $t=1..N];
[> P:='P': Function_D:=a[1]/(a[2]+a[3]*exp(-a[4]/P)):
Function_S[2]:=P*P+30:
[> P[1]:=P_Ravnoves+1: P:=P[1]: Q[1]:=evalf(Function_D):
Point_P[1]:=P_Ravnoves+1:
for t from 2 by 1 to N do
P:='P':
P[t]:=fsolve(Function_S[2]=Q[t-1], P=0..infinity);
Point[t]:=P[t];
P:=P[t];
Q[t]:=Function_D;
Point_Q[t]:=Q[t];
end do:
[> t:='t': Points_P:=[[t, Point_P[t]] $t=1..N];
Points_Q:=[[t, Point_Q[t]] $t=1..N];



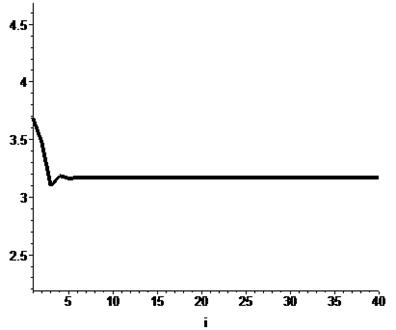
 [> plot(Points_P, i=1..N, style=line, thickness=4, color=black,
view=[1..N, P_Ravnoves-0.5..P_Ravnoves+2]);
plot(Points_Q, i=1..N, style=line, thickness=4, color=black,
view=[1..N, Q_Ravnoves-4..Q_Ravnoves+4]);
[> plot(Points_P, i=1..N, style=line, thickness=4, color=black,
view=[1..N, P_Ravnoves-0.5..P_Ravnoves+2]);
plot(Points_Q, i=1..N, style=line, thickness=4, color=black,
view=[1..N, Q_Ravnoves-4..Q_Ravnoves+4]);

|
Глава 3. Лабораторный практикум