Автоматические системы управления - динамические системы, содержащие как минимум один вход и один выход и обеспечивающие преобразование входных (задающих и возмущающих) воздействий в выходные (управляемые) переменные. В этом преобразовании могут участвовать достаточно большое число динамических элементов, называемых звеньями САУ. Характерной особенностью звеньев САУ является однонаправленность, т. е. отсутствие или ничтожное влияние выходных сигналов на входные. Данное обстоятельство позволяет осуществить декомпозицию ОУ и САУ в целом на ряд достаточно простых динамических звеньев, описываемых хорошо известными в математике методами. При этом физическая природа входных и выходных переменных звеньев может быть различной. Например, входными (управляющими) воздействиями электродвигателя постоянного тока являются напряжения на обмотках якоря и возбуждения, а выходными переменными – вращающий момент на валу двигателя и скорость вращения якоря, т. е. осуществляется преобразование электрической энергии в механическую.
Для составления уравнений элементов САУ используются фундаментальные законы природы, описываемые уравнениями Ньютона, Лагранжа, Максвелла, Ома, Кирхгофа и др. Математические модели подавляющего большинства технических ОУ уже разработаны, причем с различной степенью детализации (с различными допущениями) и подробно рассматриваются в соответствующих дисциплинах – механике, электротехнике, электромеханике, термодинамике и т. п. При этом для описания элементов САУ используют различные формы, в частности:
1. функциональные схемы и схемы замещения той или иной степени детализации, принципиальные и монтажные схемы и др.;
2. обыкновенные дифференциальные уравнения или дифференциальные уравнения в частных производных;
3. операторные уравнения, передаточные функции и матрицы (функции комплексной переменной s или оператора p Лапласа в непрерывных САУ, функции комплексной переменной z в дискретных САУ);
4. структурные схемы;
5. сигнальные графы;
6. частотные характеристики и диаграммы на их основе;
7. векторно-матричные уравнения;
8. схемы пространства состояний.
Большинство методов описания САУ базируются на теории линейных систем. Если хотя бы один элемент САУ содержит нелинейный элемент, то такая система является нелинейной и требует применения специальных методов исследования [2, 12, 19, 20, 21].
Синтез и анализ САУ осуществляют в частотной или временной области, что предполагает применение различных форм математического описания элементов САУ.
Частотные методы синтеза и анализа применимы к линейным стационарным САУ (непрерывным и дискретным) практически любой сложности. Сущность частотных методов исследования САУ заключается в оценке устойчивости и качества по установившейся реакции системы на гармоническое воздействие различной частоты (оцениваются изменение амплитуды и фазовый сдвиг выходного сигнала относительно входного). При этом переход от операторной формы представления к частотной осуществляется простейшей заменой оператора p на  в операторных уравнениях непрерывных САУ и оператора z на
в операторных уравнениях непрерывных САУ и оператора z на 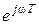 в операторных уравнениях дискретных САУ. Наиболее часто для описания и исследования САУ частотными методами применяют:
в операторных уравнениях дискретных САУ. Наиболее часто для описания и исследования САУ частотными методами применяют:
- логарифмические амплитудно- и фазо-частотные характеристики (ЛАЧХ и ЛФЧХ) разомкнутой САУ, образующие диаграмму Боде (позволяют оценить абсолютную и относительную устойчивость – запасы по модулю и фазе замкнутой САУ, а также полосу пропускания контура, частоту резонанса и другие характеристики);
- амплитудно-фазовую характеристику (АФХ) разомкнутой САУ - диаграмму Никольса (позволяет оценить абсолютную и относительную устойчивость замкнутой САУ и косвенно ряд других показателей);
- диаграмму (годограф) Найквиста разомкнутой САУ (позволяет оценить абсолютную и относительную устойчивость замкнутой САУ).
Временные методы синтеза и анализа САУ применимы к линейным и нелинейным, стационарным и нестационарным, непрерывным и дискретным, одно- и многомерным САУ любой сложности. Сущность временных методов анализа заключается в получении прямых или косвенных показателей качества управления по реакции САУ на типовой тестовый сигнал (в виде единичной ступенчатой функции или дельта-функции). Прямые оценки качества регулирования обычно определяют по виду переходной характеристики (время регулирования, время нарастания регулирования, перерегулирование, время запаздывания, частота установившихся колебаний, коэффициент затухания колебаний). К косвенным оценкам качества САУ относят корневые, частотные оценки качества, а также интегральные, в том числе интегральные квадратичные оценки. Они же лежат в основе формальных оптимизационных процедур синтеза САУ.
При исследовании САУ временными методами применяют решение тем или иным методом систем обыкновенных дифференциальных уравнений, описывающих элементы САУ и связи между ними, относительно заданных переменных с использованием средств вычислительной техники. Наибольшее применение нашли методы Эйлера 1-го порядка, Рунге-Кутта 4-го и 5-го порядка, а также метод переходных состояний, позволяющий практически с любой требуемой точностью осуществить переход САУ из произвольного начального состояния в следующее состояние, отстоящее на период, заданный в матрице перехода. Последний из методов базируется на векторно-матричном аппарате исследования систем и ориентирован на применение цифровой вычислительной техники (персональных компьютеров) и соответствующих программных систем и математических пакетов расширения.
Заметим, что, хотя между свойствами САУ во временной и частотной областях отсутствует прямая связь, по виду частотных характеристик можно во многом судить о поведении системы во временной области. Целесообразность применения того или иного метода исследования САУ не всегда очевидна и требует обоснования. Применительно к сложным многомерным нестационарным САУ целесообразность применения временных методов исследования и современных вычислительных средств не вызывает сомнений.
4.2. Статические и динамические характеристики САУ
Статические режимы САУ характеризуются установившимися состояниями при неизменных входных воздействиях. Уравнения статики легко получить из уравнений динамики САУ путем приравнивания в них нулю всех производных по времени переменных (координат состояния) и внешних воздействий. В операторных уравнениях и на структурных схемах (см. гл. 5) линейных САУ это эквивалентно нулевой частоте изменения переменных, что достигается приравниванием нулю оператора p.
Таким образом, статическая характеристика системы – это зависимость выходной переменной от какой-либо входной переменной в статическом (установившемся) режиме.
Примером статической характеристики является механическая характеристика двигателя постоянного тока (ДПТ) – зависимость угловой частоты вращения вала двигателя от момента нагрузки на валу в установившихся режимах (рис. 4.1). Как видим, при увеличении нагрузки на валу двигателя скорость вращения вала двигателя падает и появляется статическая ошибка регулирования скорости. При изменении нагрузки от нуля до номинального значения M сн скорость вращения уменьшается от скорости холостого хода  до номинальной скорости
до номинальной скорости  .
.
В номинальном режиме статическая ошибка регулирования скорости вращения
 . (4.1)
. (4.1)

Рис. 4.1. Статическая механическая
характеристика ДПТ
Найдем выражения для установившейся ошибки регулирования при изменении задающих или возмущающих воздействий линейной системы управления.
Передаточная функция любой замкнутой линейной САУ с отрицательной обратной связью (рис. 4.2) определяется передаточными функциями прямого 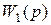 и обратного
и обратного  каналов регулирования (см. гл. 5.3)
каналов регулирования (см. гл. 5.3)
 . (4.2)
. (4.2)

Рис. 4.2. Структурная схема
замкнутой САУ
Отсюда изображение ошибки регулирования в системе
 , (4.3)
, (4.3)
а передаточная функция по ошибке
 . (4.4)
. (4.4)
Как следует из (4.3), ошибка регулирования будет стремиться к нулю при X = const, если  , что предполагает реализацию бесконечно большого усиления в устройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению ненулевой статической ошибки регулирования.
, что предполагает реализацию бесконечно большого усиления в устройстве управления и может привести к неустойчивости системы. Кроме того, реальные динамические звенья обладают конечными коэффициентами усиления, что приводит к возникновению ненулевой статической ошибки регулирования.
Между тем, статическая ошибка регулирования в системе при неизменном входном воздействии может быть сведена к нулю, если сделать равной нулю передаточную функцию ошибки  по задающему или возмущающему воздействию при p =0. Для этого достаточно в прямой или обратный канал регулирования системы, приведенной два рис. 4.2, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру устройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает
по задающему или возмущающему воздействию при p =0. Для этого достаточно в прямой или обратный канал регулирования системы, приведенной два рис. 4.2, ввести интегрирующее звено. На практике интегрирующее звено вводят в структуру устройства управления, применяя И-, ПИ-, ПИД-регуляторы. Это обеспечивает 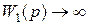 и, тем самым нулевую статическую ошибку регулирования. Такие системы принято называть астатическими первого порядка по задающему или (и) возмущающему воздействию. Для придания системе астатизма более высокого порядка в структуру регулятора вводят соответствующее число интеграторов.
и, тем самым нулевую статическую ошибку регулирования. Такие системы принято называть астатическими первого порядка по задающему или (и) возмущающему воздействию. Для придания системе астатизма более высокого порядка в структуру регулятора вводят соответствующее число интеграторов.
Величина установившейся ошибки регулирования, наличие и порядок астатизма замкнутой САУ определяются не только ее моделью, но и видом входного сигнала. Определим, как вид входного воздействия влияет на величину установившейся ошибки.
Передаточную функцию прямого канала запишем в виде
 , (4.5)
, (4.5)
где K – коэффициент передачи,
zi, pj – полюсы и нули передаточной функции (4.5).
Для определения величины установившейся ошибки рассмотрим случай единичной обратной связи, т. е.  =1.
=1.
В установившихся режимах (при p = 0) передаточную функцию (4.4) можно записать в виде
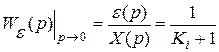 , (4.6)
, (4.6)
где Ki – коэффициент ошибки системы, определяемый видом входного воздействия, i = 0, 1, 2.
Поскольку в качестве типовых тестовых сигналов применяют ступенчатое, линейное и квадратичное входное воздействие, то для оценки установившихся ошибок в системе выделяют 3 типа коэффициентов ошибок:
1) коэффициент ошибки по положению (i = 0)
 ; (4.7)
; (4.7)
2) коэффициент ошибки по скорости (i = 1)
 ; (4.8)
; (4.8)
3) коэффициент ошибки по ускорению (i = 2)
 . (4.9)
. (4.9)
Как следует из выражений (4.3)…(4.9), установившиеся ошибки САУ могут иметь нулевое, бесконечное или постоянное значение в зависимости от числа интеграторов в передаточной функции W 1(p) и типа входного сигнала. Установившиеся ошибки для трех типов входных воздействий и трех типов передаточной функции W 1(p) – с отсутствием интеграторов, с одним и двумя интеграторами – приведены в табл. 4.1.
Таблица 4.1
| Число интеграторов | Входной сигнал | ||
Ступенчатый


| Линейный

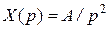
| Квадратичный
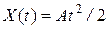

| |

| 
| 
| |

| 
| 
| |

| 
| 
|
Динамические режимы САУ характеризуются переходными состояниями системы при изменении входных (задающих и возмущающих) воздействий. При этом различают свободные и вынужденные переходные процессы.
Назовем процесс вынужденным, если промежуток времени между моментом t з (t в) приложения задающего (возмущающего) воздействия X (t) и моментом наблюдения выходной величины Y (t) равен бесконечности. В дальнейшем будем полагать моменты времени приложения воздействий равными нулю. Тогда процесс изменения выходной величины Y (t) в соответствие с теоремой свертывания (умножения изображений) будет иметь вид [19]
 , (4.10) где
, (4.10) где  - импульсная переходная функция по внешнему (задающему или возмущающему) воздействию.
- импульсная переходная функция по внешнему (задающему или возмущающему) воздействию.
Свободный (собственный) процесс в системе определяется решением однородного дифференциального уравнения, описывающего САУ. Он протекает под действием ненулевых начальных условий Y (t 0) и в устойчивых системах асимптотически затухает:
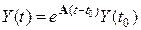 , (4.11)
, (4.11)
где  – матрица перехода системы из начального состояния Y (t 0) в текущее состояние Y (t). Понятие и расчет матрицы перехода рассмотрены в гл. 9.3.
– матрица перехода системы из начального состояния Y (t 0) в текущее состояние Y (t). Понятие и расчет матрицы перехода рассмотрены в гл. 9.3.
Полное решение уравнения движения линейных САУ представляет собой сумму решений уравнений свободного и вынужденного движений.
В качестве примера на рис. 4.3 приведена реакция электродвигателя постоянного тока (полное решение уравнения движения) на ступенчатое приложение номинальной нагрузки M сн(возмущающего воздействия) к его валу.
При приложении нагрузки скорость 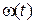 двигателя падает, причем имеет место колебательный процесс. Максимальный динамический провал скорости
двигателя падает, причем имеет место колебательный процесс. Максимальный динамический провал скорости 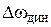 превышает статическое падение скорости
превышает статическое падение скорости  (см. рис. 4.1).
(см. рис. 4.1).

Рис. 4.3. Реакция электродвигателя
на возмущающее воздействие
в виде ступени нагрузки на валу
Вынужденное движение соответствует новому установившемуся состоянию - номинальной скорости  электродвигателя. Время переходного процесса (перехода в новое установившееся состояние) составляет t р .
электродвигателя. Время переходного процесса (перехода в новое установившееся состояние) составляет t р .
4.3. Переходные и импульсные характеристики САУ
|
Временные характеристики линейной САУ (динамического звена) могут быть определены по ее переходной и импульсной переходной функции.
Одним из наиболее распространенных тестовых воздействий на систему является единичное ступенчатое воздействие x ( t ), которое может быть представлено в виде функции
 (4.12)
(4.12)
или в виде графика, приведенного на рис. 4.4.

Рис. 4.4. Единичное ступенчатое воздействие
на систему
Следует отметить, что ступенчатое воздействие на входе САУ это не только типовое тестовое воздействие. Оно относится к одному из наиболее распространенных программно-временных задающих воздействий, прежде всего, в системах цифрового управления, задающие и управляющие воздействия которых квантованы по уровню.
Переходная функция (переходная характеристика) h ( t ) – это нормальная реакция системы (переходный процесс), вызванная входным единичным ступенчатым воздействием при нулевых начальных условиях. Переходные функции САУ определяют, как правило, по формулам Хевисайда или методом математического моделирования. Для наиболее широко распространенных динамических звеньев САУ имеются аналитические выражения их переходных функций [2, 12, 19].
Импульсная единичная функция (дельта-функция Дирака) относится также к тестовым сигналам САУ, характеризующим ее свойства во временной области. Она представляет собой производную от единичной ступенчатой функции
 . (4.13)
. (4.13)
Дельта-функцию можно трактовать как бесконечно короткий по времени импульс с бесконечно большой амплитудой, но с конечной площадью, равной единице.
Нормальная реакция САУ на импульсное воздействие – импульсная переходная функция (весовая функция) w ( t )системы. Ее легко получить численным или графическим дифференцированием переходной функции. Для наиболее широко распространенных динамических звеньев САУ в учебниках по теории управления приводятся аналитические выражения их весовых функций [2, 12, 19-21].
Переходные и весовые функции типовых элементарных динамических звеньев приведены в главе 5.
4.4. Уравнение Лагранжа 2-го рода и дифференциальные
уравнения
Математические модели технических средств, систем автоматизации и управления весьма многообразны и могут быть достаточно сложными. В частности, на сложность электромеханических систем управления влияет множество факторов: число, тип и последовательность звеньев (кинематических пар), компоновочные схемы размещения приводов механических подсистем и конструкции передаточных механизмов, наличие устройств уравновешивания и динамической развязки движений и др. Для определения их математических моделей, в общем случае, применяют весьма сложные уравнения Лагранжа-Максвелла.
Механические системы, как правило, имеют значительно большую инерционность по сравнению с инерционностью электромагнитных цепей электроприводов, приводящих их в движение, что позволяет при составлении математических моделей механических систем в форме дифференциальных уравнений использовать более простые уравнения Лагранжа 2-го рода [19]:
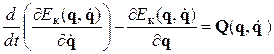 , (4.14) где q,
, (4.14) где q,  ,
, 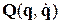 – векторы обобщенных координат, скоростей и обобщенных сил;
– векторы обобщенных координат, скоростей и обобщенных сил;
 – кинетическая энергия механической системы.
– кинетическая энергия механической системы.
Решение уравнения (4.14), т. е. математическую модель механического объекта управления представляют в форме системы обыкновенных дифференциального уравнений, разрешенных относительно вторых производных обобщенных координат (обобщенных ускорений), т. е.
 . (4.15)
. (4.15)
Для составления уравнений Лагранжа составляют расчетную схему механической системы, учитывающую геометрические размеры механических звеньев, тип и распределение (порядок расположения) кинематических пар, массы звеньев, упругие свойства кинематических связей.
Составление дифференциальных уравнений движения материальной системы на основе уравнений Лагранжа проводят в следующей последовательности:
1) определяют число n степеней свободы материальной системы;
2) выбирают систему координат и вводят независимые обобщенные координаты q 1, q 2 ,…, qn;  - вектор обобщенных координат; их число должно быть равно числу n степеней свободы механической системы;
- вектор обобщенных координат; их число должно быть равно числу n степеней свободы механической системы;
примечание: обобщенные координаты – независимые параметры, однозначно определяющие положение точек материальной системы;
3) определяют обобщенные силы системы Q 1, Q 2,…, Qn;  - вектор обобщенных сил;
- вектор обобщенных сил;
примечание 1: для определения обобщенной силы Qi, соответствующей i -й обобщенной координате, надо вычислить сумму работ всех активных сил, включая реакции неидеальных связей, на обобщенном возможном перемещении  ; при этом все остальные обобщенные возможные перемещения принимают равными нулю; тогда
; при этом все остальные обобщенные возможные перемещения принимают равными нулю; тогда
 ; (4.16)
; (4.16)
примечание 2: если силы, действующие на систему потенциальны (однозначно определяются только положением материальных точек системы), то обобщенную силу Qi можно найти как частную производную потенциальной энергии по обобщенным координатам, т. е.
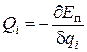 , (4.17)
, (4.17)
где потенциальная энергия системы E п определяется как функция обобщенных координат, т. е. E п =  ; потенциальная энергия, создаваемая силами тяжести звеньев механической системы, для i -го звена массой mi равна
; потенциальная энергия, создаваемая силами тяжести звеньев механической системы, для i -го звена массой mi равна  , где
, где  - высота подъема центра масс i -го звена, g – ускорение силы тяжести; потенциальная энергия, создаваемая силами упругости упругого звена (например, пружины), для i -го звена равна
- высота подъема центра масс i -го звена, g – ускорение силы тяжести; потенциальная энергия, создаваемая силами упругости упругого звена (например, пружины), для i -го звена равна  , где сi – жесткость упругого звена,
, где сi – жесткость упругого звена,  - угол закручивания (приращение обобщенной координаты);
- угол закручивания (приращение обобщенной координаты);
4) вычисляют кинетическую энергию E к системы как функцию обобщенных координат и скоростей т. е.  ; кинетическая энергия материальной системы определяется как сумма кинетических энергий всех n материальных точек системы
; кинетическая энергия материальной системы определяется как сумма кинетических энергий всех n материальных точек системы
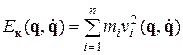 . (4.18)
. (4.18)
Использование формулы (4.18) ориентировано на концепцию распределенных масс механической системы и требует определение абсолютных скоростей  достаточно большого множества материальных точек системы с массами mi.
достаточно большого множества материальных точек системы с массами mi.
Кинетическая энергия в частных случаях движения твердого тела:
- при поступательном движении:  , где m – масса твердого тела, v – скорость любой его точки;
, где m – масса твердого тела, v – скорость любой его точки;
- при вращательном движении вокруг неподвижной оси: 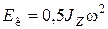 , где JZ – момент инерции твердого тела относительно оси Z вращения,
, где JZ – момент инерции твердого тела относительно оси Z вращения, 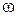 – угловая скорость вращения;
– угловая скорость вращения;
- при вращательном движении вокруг неподвижной точки:  , где J – момент инерции твердого тела относительно мгновенной оси вращения,
, где J – момент инерции твердого тела относительно мгновенной оси вращения,  – модуль мгновенной угловой скорости.
– модуль мгновенной угловой скорости.
Если в твердом теле удается выделить оси материальной симметрии и, соответственно, главные центральные оси инерции, то кинетическую энергию тела определяют по формуле
 , (4.19)
, (4.19)
где 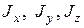 - осевые моменты инерции твердого тела;
- осевые моменты инерции твердого тела;
 - проекции мгновенной угловой скорости на соответствующие координатные оси.
- проекции мгновенной угловой скорости на соответствующие координатные оси.
5) определяют частные производные кинетической энергии по обобщенным скоростям, т. е. 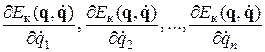 , а затем вычисляют их производные по времени:
, а затем вычисляют их производные по времени:
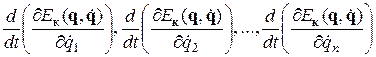 ;
;
6) находят частные производные кинетической энергии по обобщенным координатам, т. е.  ;
;
7) полученные в п. п. 3-6 результаты подставляют в уравнение (4.14) и дифференциальные уравнения разрешают относительно вторых производных по времени обобщенных координат, т. е. записывают уравнение движения механической системы в форме (4.15).
В качестве примера составления уравнения Лагранжа рассмотрим кинематическую схему маятника, приведенную на рис. 4.5.

Рис. 4.5. Кинематическая схема маятника
1) Число степеней свободы материальной системы n = 1.
2) В качестве обобщенной координаты механической системы примем угол  отклонения нити маятника от вертикальной оси.
отклонения нити маятника от вертикальной оси.
3) Для определения обобщенной силы Q 1(n =1) надо вычислить сумму работ всех активных сил, включая реакции неидеальных связей, на обобщенном возможном перемещении  . Единственной активной силой является сила тяжести маятника P = mg. Так как нить рассматривается нерастяжимой, то она является идеальной связью. Работа силы тяжести на возможном перемещении
. Единственной активной силой является сила тяжести маятника P = mg. Так как нить рассматривается нерастяжимой, то она является идеальной связью. Работа силы тяжести на возможном перемещении  :
:
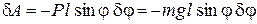 .
.
Заметим, что работа является отрицательной, т. к. знаки вращающего момента, вызванного силой P и приращения  , разные.
, разные.
Отсюда с учетом (4.16)
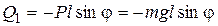 .
.
Полученная обобщенная сила имеет размерность момента (нм).
Обобщенная сила Q 1 может быть определена иначе - на основе расчета потенциальной энергии системы  :
:
 .
.
4) Кинетическая энергия системы (твердого тела с массой m) при вращательном движении вокруг неподвижной оси:
 ,
,
где JZ – момент инерции твердого тела относительно оси Z вращения, направленной перпендикулярно плоскости рисунка; для невесомой нити и точечной массы m имеем  ;
;
 – угловая скорость вращения.
– угловая скорость вращения.
5) Частная производная кинетической энергии по обобщенной скорости  , а ее производная по времени
, а ее производная по времени
 .
.
6) Кинетическая энергия E к не зависит от обобщенной координаты  , а, следовательно, частная производная кинетической энергии по обобщенной координате
, а, следовательно, частная производная кинетической энергии по обобщенной координате  .
.
7) После подстановки полученных выражений в уравнение Лагранжа (4.14) получим
 (4.20)
(4.20)
или с учетом допущений, принятых для нити и массы маятника
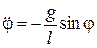 . (4.21)
. (4.21)
Полученные дифференциальные уравнения (4.20), (4.21) являются динамическим уравнением движения маятника.
4.5. Линеаризация САУ
При анализе и синтезе САУ применяются математические модели (ММ), представляемые, как правило, обыкновенными дифференциальными уравнениями (ОДУ). Большинство реальных ОУ в широком диапазоне изменения их переменных являются нелинейными, однако, как показывает практика, в области достаточно малых отклонений координат (переменных) они могут быть аппроксимированы линейными ММ. Свойство линейности ММ ОУ позволяет при исследовании САУ воспользоваться преобразованием Лапласа к ММ в форме ОДУ и свести интегрирование ОДУ к простым алгебраическим преобразованиям. Кроме того, линейность преобразований и получаемых линейных подпространств координат лежит в основе векторно-матричных моделей САУ и их исследования в пространстве состояний, т. е. во временной области. Последнее обстоятельство позволяет применить при синтезе и анализе САУ упоминаемые ранее компьютерные системы MATLAB, MathCAD, Maple V, Mathematica и др., базирующиеся на матричных методах исследования линейных систем.
Любая линейная системаудовлетворяет свойствам суперпозиции и гомогенности. Первое свойство означает, что произвольная сумма аддитивных воздействий x 1(t) + x 2(t) на входе САУ дает реакцию y 1(t) + y 2(t) на выходе САУ. Второе свойство предполагает выполнение условия масштабируемости, т. е. при изменении входного сигнала x 1 в k раз выходной сигнал y 1 линейной САУ изменится соответственно в k раз.
Подавляющее большинство механических и электрических элементов САУ являются линейными в достаточно широком диапазоне изменения их переменных (координат) относительно стационарного режима, чего нельзя сказать о гидравлических, пневматических, термодинамических и иных элементах. Вместе с тем, даже такие элементы САУ можно линеаризовать при условии достаточно малых отклонений координат в окрестности точки стационарного режима (рабочей точки).
Любую непрерывную функцию y (x) в окрестности рабочей точки x = x 0 можно разложить в ряд Тейлора
 (4.22)
(4.22)
В окрестности рабочей точки при малых отклонениях переменной x от x 0 выражение (4.22) можно аппроксимировать линейной формой
 , (4.23)
, (4.23)
где k – тангенс угла наклона касательной к кривой  в точке x 0.
в точке x 0.
Выражение (4.23) можно преобразовать к виду
 (4.24)
(4.24)
или
 . (4.25)
. (4.25)
Данный метод линеаризации иногда еще называют методом касательной линеаризации в рабочей точке x 0 или вдоль рабочей траектории  .
.
Рассмотрим простейший пример линеаризации модели идеального маятника как статического элемента САУ (см. рис. 4.4).
Уравнение движения маятника, отклоненного на угол  от вертикали, в осях “угол - вращающий момент” в соответствие с (4.20) имеет вид
от вертикали, в осях “угол - вращающий момент” в соответствие с (4.20) имеет вид
 , (4.26) где M – вращающий момент;
, (4.26) где M – вращающий момент;
g – ускорение свободного падения.
Линеаризуем (4.26) в окрестности рабочей точки M 0( ), где
), где  примем равным нулю:
примем равным нулю:
 (4.27)
(4.27)
или 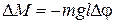 . (4.28)
. (4.28)
Рассмотрим пример линеаризации нелинейного уравнения, описывающего зависимость электромагнитного момента M двигателя постоянного тока от тока якоря i я и магнитного потока Ф,
M = C м Ф i я, (4.29)
где C м – конструктивная постоянная двигателя.
Уравнение (4.29) относится к классу нелинейных уравнений, поскольку содержит произведение координат электродвигателя – магнитного потока и тока якоря. Линеаризуем (4.29) в окрестности рабочей точки M 0(Ф 0, i я0), соответствующей, например, номинальному режиму работы двигателя, т. е. при M 0 = M н, Ф 0 = Ф н, i я0 = i ян:
 . (4.30)
. (4.30)
Пренебрегая в (4.30) произведением приращений координат получим линеаризованное уравнение в приращениях
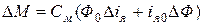 . (4.31)
. (4.31)
В этом уравнении Ф 0 и i я0 предполагаются величинами постоянными, а, следовательно, уравнение (4.31) относится к классу линейных (линеаризованных в рабочей точке) уравнений.
Если управление двигателем осуществляется одновременно по цепям якоря и магнитного потока (цепи возбуждения двигателя), то рабочая точка в процессе управления будет смещаться относительно начального (номинального) режима, образуя семейство рабочих точек или рабочую траекторию. В этом случае при применении уравнения (4.31) говорят о линеаризации исходного нелинейного уравнения (4.29) вдоль рабочей траектории
M 0 = Cм Ф 0 i я0.
Помимо касательной линеаризации при исследовании нелинейных САУ в частотной области применяют метод гармонической линеаризации, а при исследовании стохастических САУ - стохастической линеаризации [2, 12, 19, 20].
5. Структурные методы исследования линейных САУ
Исследование линейных динамических систем, математические модели которых представлены в форме обыкновенных дифференциальных уравнений, может быть упрощено, если вместо рассмотрения переменных, характеризующих состояние системы во времени (оригиналов), рассматривать соответствующие им изображения, получаемые на основе преобразования Лапласа. Применение такого подхода позволяет заменить операции дифференцирования и интегрирования более простыми арифметическими операциями умножения и деления изображения на оператор p и, тем самым, значительно облегчить исследование САУ. Преобразования Лапласа лежат в основе получения передаточных функций линейных динамических звеньев, объектов и систем управления. Они также являются основой составления и преобразования структурных схем – удобной и наглядной форме структурного описания и исследования динамических свойств линейных САУ.
5.1. Преобразование Лапласа, передаточные функции и матрицы
Возможность линеаризации технических объектов и систем предоставляет в распоряжение исследователей аппарат преобразования Лапласа.
Прямое преобразование Лапласа (определение изображения) непрерывной функции времени f (t) имеет вид [2, 19]
 , (5.1)
, (5.1)
где p – оператор Лапласа (комплексная переменная).
Обратное преобразование Лапласа (определение оригинала) функции комплексной переменной F (p) имеет вид
 . (5.2)
. (5.2)
При решении большинства практических задач применяются таблицы преобразований Лапласа, полученные на основе выражения (5.1). В табл. 5.1 приведены некоторые наиболее важные соотношения непрерывной функции времени t и функции комплексной переменной p.
Как видим, переменную p в преобразовании Лапласа можно рассматривать как оператор дифференцирования при описании САУ во временной области, т. е.
 . (5.3)
. (5.3)
Таблица 5.1
| Наименование функции | Оригинал функции f (t) | Изображение функции F (p) | ||
| Импульсная | 
| |||
| Импульсная с чистым запаздыванием | 
| 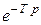
| ||
| Ступенчатая | 
| 
| ||
| Линейная | 
| 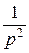
| ||
| Степенная | 
| 
| ||
| Асимптотически затухающая | 
| 
| ||
| Асимптотически нарастающая | 
Поиск по сайту©2015-2026 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-16 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд Интересно: |