(управления).
Применяется к уравнениям вида (6), где f – непрерывная вектор-функция,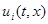 
- скалярная функция, разрывная только на гладкой поверхности 
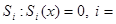1,…, r. Допускоются пересечения и даже совпадения этих поверхностей.
В точках, принадлежащих одной или одновременно нескольким поверхноостям, например 
,…, Sm (
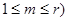, полагают (если решение не может сойти тут же с такой поверхности или с пересечения этих поверхностей)
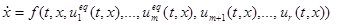, (8)
где эквивалентные управления 
определяются так, чтобы вектор 
в (8) касался поверхностей ,…, Sm и чтобы значение 
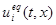содержалось в отрезке с концами 
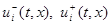, где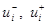 
– предельные значения функции 
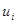с обеих сторон поверхности 
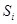, i= 1,…, m. Т.о., функции 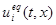определяются из системы уравнений
.
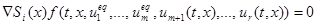Определение 5.
Решением (6) называется абсолютно непрерывная вектор-функция, которая вне поверхностей 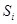удовлетворяет уравнению (6), а на этих поверхностях и их пересечениях – уравнениям вида (8) (при почти всех t).
Например, в случае 
конец вектора 
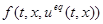лежит на пересечении касательной к S в точке x с дугой abc, которую пробегает конец вектора f(t,x,u), когда u изменяется от 
до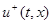 
:
 |
Рис. 4.
С геометрической точки зрения, метод эквивалентного управления предполаглет замену разрывного управления на границе разрыва, где оно не определено, ненпрерывным управлением, которое направляет вектор скорости в пространстве состояний системы вдоль пересечения поверхностей разрыва. Например, в системе c одной поверхностью разрыва 
для нахождения этого вектора в некоторой точке (t, x) нужно построить годограф f(t, x, u), изменяя скалярное управление от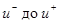 
, и найти точку его пересечения с касательной плоскостью. Точка пересечения определяет 
диф. уравнения (8) (для r =1 (8) примет вид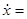 
).
 |
|
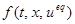Уравнение (6), доопределенное указаным образом, сводится к диф. включению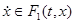 
. Множество 
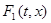определено в (7), где 
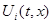– отрезок с концами 
и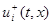 
; для тех 
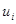, которые непрерывны в точке (t,x), 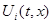является точкой .
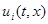Правая часть (8) есть вектор с концом в точке пересечения множества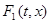 
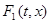с касательной к пересечению поверхностей ,…, Sm. На рис. 4 множество – дуга abc, а правая часть (8) – вектор xb.
Доопределение А было обосновано лишь для скалярного случая (u - скалярная функция) и лишь с помощью предельных переходов для частных случаев неидеальностей, доопределение Б применимо и в случае векторной разрывной динамической системы (т.е. управляющее воздействия приложены к различным точкам объекта и управление u является векторной величиной), описываемой уравнениями
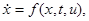(9)
x,f - n -мерные векторы-столбцы,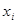 
- координаты системы, 
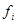- непрерывные функции по всем аргументам (
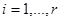), u - m -мерный вектор-столбец, каждая компонента которого 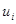претерпевает разрывы на поверхности 
:
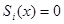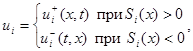
i= 1, …, m, 
, 
(
), 
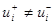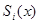- непрерывные функции. Если положить 
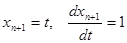, то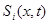 
.
Для доопределения уравнений идеального скольжения используют метод эквивалентного управления [7]: в уравнение модели (9) вместо 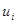подставить 
, которые являются решениями уравнения
,
где строки матрицы G ={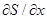 
} размерности 
являются градиентами функций 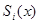. Очевидно, что при начальном значении 
в силу условия (10) дальнейшее движение будет происходить по траекториям, лежащим на многообразии S(x)= 0.
Пример 5.
Получить уравнение скольжения для разрывной системы:
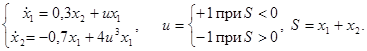
В любой точке прямой разрыва S= 0 (т.е. при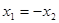 
) выполняются условия возникновения скользящего режима 
, а уравнение метода эквивалентного управления (10) имеет вид:
.
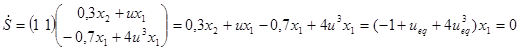Найдем эквивалентное управление из уравнения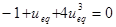 
, откуда 
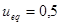, подставим его в первое уравнение системы (учитывая 
):
Замечание.
Метод Филиппова, примененный к рассматриваемой системе, согласно (4) приводит к уравнению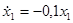 
движения по прямой S= 0.
В. Общее дополнение.
Оно применяется к уравнениям вида (6), где функция f непрерывна по t,x,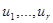 
, а каждая из функций 
разрывна только на поверхности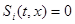 
, i =1,…, r.
Пусть 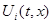и 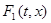те же, что в Б, а 
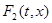– наименьшее выпуклое замкнутое множество, содержащее множество .
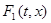Определение 6.
Решением уравнения (6) называется решение включения
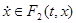(10)
Движение по поверхности разрыва S (S(x)=0) может происходить только со скоростью 
, где K(t,x) – пересечение множества с плоскостью, касательной к S в точке x. На рис. 4 множество 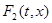- наименьшее выпуклое замкнутое множество, содержащее дугу abc. Если эта дуга лежит в одной плоскости, то множество 
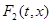– сегмент между этой дугой и ее хордой, заштрихованный на рисунке, а K(t,x) – отрезок, являющийся пересечением этого сегмента с касательной к S в точке x.
Если функция f нелинейна по 
, то, вообще говоря, множество K(t, x) содержит более одной точки и скорость движения по S определяется неоднозначно.
Сравнение определений.
Сравним определения А, Б, В.
Уравнение (6) можно записать в виде (1) и применить к нему определение А. Т.к. при этом множнство 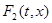содержит множества 
и 
из (2) и (7), то каждое решение в смысле определения А и каждое решение в смысле определения Б являются так же решением в смысле определения В. Обратно, вообще говоря, неверно: на рис. 4 множество F – хорда ac,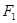 
- дуга abc, 
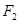- заштрихованный сегмент.
Если же функция f линейна п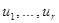о 
, то 
и определения Б и В совпадают. Если, кроме того, все поверхности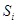 
различны и в точках их пересечения векторы нормалей линейно независимы, то множества F, 
и 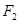совпадают, тогда совпадают и все три определения А, Б, В.
Глава III
Исследование устойчивости для дифференциальных
уравнений с разрывными правыми частями.
§1.Определение устойчивости. Метод функций Ляпунова.
Теория устойчивости создана в 90-х годах 19 в. А.М. Ляпуновым (в 1892 г. появилась знаменитая докторская диссертация “Общая задача об устойчивости движения”). Эта теория нашла широкое применение не только в математике, механике, технике, но и в химии, термодинамике, синергетике. Очень бльшую роль играет решение прроблемы устойчивости движения в небесной механике. На теории Ляпунова базируется современная наука о полете искусственных спутников Земли.
Определение устойчивости и асимптотической устойчивости решений диф. уравнений с непрерывной правой частью приводится, например, в [4]. Теория устойчивости движения занимается исследованием влияния возмущающих факторов на движение матариальной системы (под возмущающим фвкторами понимают силы, не учитываемые при написании движения вследствие их малости по сравнению с основными силами); устойчивость по Ляпунову – это близость законов изменения состояния во времени для невозмущенного и возмущенного движений. Сводя вопрос устойчивости невозмущенного движения к вопросу устойчивости положения равновесия, А.М. Ляпунов связывал факт устойчивости или неустойчивости с наличием функции V(t, x) – функции Ляпунова, производная которой по времени, взятая согласно системе диф. уравнений, обладает определенными свойствами. Метод функций Ляпунова является одним из наиболее эффективных методов исследования систем автоматического управления. Значение этого метода далеко не исчкрпывается возможностью установления факта устойчивости или неустойчивости исследуемой системы. Но в данной работе ограничимся только этим.
Метод функций Ляпунова переносится и на случай разрывной правой части системы
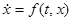. (1)
Как было показано в первой главе, уравнения (1) сводятся к диф. включениям
(2)
Для диф. включений имеются два типа устойчивости: устойчивость и слабая устойчивость.
Определение 1.
Решение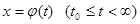 
дифференциального включения (2) называется устойчивым (соответственно слабо устойчивым), если для каждого 
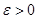существует такое 
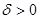, что для каждого такого 
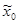, что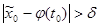 
, каждое решение (соответственно некоторое решение) 
с начальным условием 
при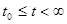 
существует и удовлетворяет неравенству
(
).
Асимптотическая устойчивость и слабая асимптотическая устойчивость определяются аналогично, но с дополнительным условием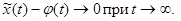 
Пример 1.
(
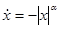). Решение 
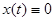асимптотически устойчиво. При 
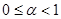любое другое решение достигает положения равновесия x= 0 за конечное время, а при 
за бесконечное время.
Пример 2.
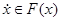, F(x) – отрезок с концами kx и mx. 
- решение. Для других решений имеем
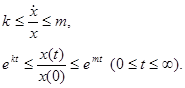
При 
асимптотически устойчиво,
при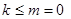 
устойчиво,
при 
слабо асимптотически устойчиво,
при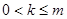 
неустойчиво.
Для диф. уравнений с непрерывной правой частью известны теоремы Ляпунова об устойчивости и об асимптотической устойчивости [4]. В работе [17] сформулированы подобные теоремы для разрывных систем (1). Но для таких уравнений функция Ляпунова V(t,x) может не принадлежать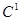 
.
Для функции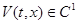 
(т.е. имеются непрерывные производныепервого порядка) определяются верхняя и нижняя производные в силу диф. включения (2):
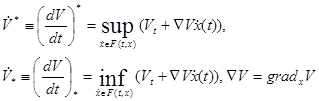
При почти всех t производная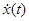 
существует и удовлетворяет включению (2). При этих t существует
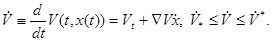(3)
Теорема 1.
Пусть в замкнутой области D (
) для всех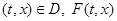 
- непустое, ограниченное, замкнутое, выпуклое множество и функция 
-непрерывна по t, x; 
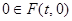и существуют функции 
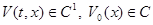, для которых 
.
Тогда:
1) Если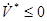 
в D, то решение 
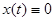включения (2) устойчиво.
2) Если, кроме того, существуют функции 
причем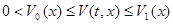 
, 
, (
), 
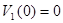, то решение 
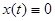асимптотически устойчиво.
Известные доказательства этих утверждений для диф. уравнений [4] остаются справедливыми и для диф. включений; при этом для оценки сверху функции V(t, x(t)) используют соотношение (3).
Теорема 2.
Если выполнены условия теоремы 1, но с заменой 
, то решение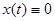 
слабо устойчиво в случае 1) и слабо асимптотически устойчиво в случае 2).
Доказательство теоремы 2 приведено в [17].
Рассмотрим теперь случай, когда функция Ляпунова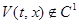 
, но удовлетворяет условию Липшица в окрестности каждой точки области D. Тогда для любой абсолютно непрерывной функции x(t), значит и для любого решения, сложная функция V(t, x(t)) абсолютно непрерывна и почти всюду имеет производную по t. Однако решение может в течение некоторого промежутка времени идти по линии или поверхности, на которой grad V не существует, и производную dV/dt, нельзя, как в случае 
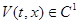, представить в виде
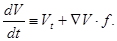
Для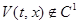 
:
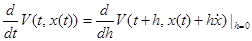. (4)
В случае функции V(t, x), удовлетворяющей условию Липшица, верхнюю и нижнюю производные 
от функции V в силу включения (2) можно определить как sup и inf правой части (4) по всем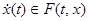 
. Тогда теоремы 1и 2 сохраняются.
Пример 3.
Если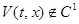 
, то нельзя пренебрегать отысканием dV/dt на линиях поверхностях разрыва функции f(t, x) даже в случае доопределения А.
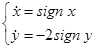
Но этого недостаточно для применения теоремы 1, т.к. производные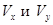 
разрывны на осях координат, т.е. там же, где разрывны правые части системы. На оси Ox при доопределении А:
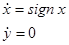
, и условия теоремы 1 не выполнены. Тот же результат получается по формуле (4) при h =0:
.
Т.к. на оси Ox имеем 
, то решения по оси удаляются от точки (0, 0) со скоростью 1 и решение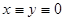 
неустойчиво
§2. Некоторые сведения теории дифференциальных
уравнений с импульсным воздействием.
При математическом описании эволюции процессов с кратковременными возмущениями часто длительностью возмущения пренебрегают и считают, что эти возмущения носят “мгновенный” характер. Такая идеализация приводит к необходимости исследовать динамические системы с разрывными траекториями или, как их еще называют, диф. уравн. С импульсным воздействием.
Определение таких систем приведено [12], они задаются
а) системой диф. уравн.
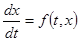(5)
б) некоторым множествам Ft, заданным в расширенном фазовом пространстве,
в) оператором At, заданным на множестве Ft и отображающем его на множество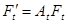 
.
Сам процесс происходит следующим образом: изображающая точка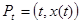 
, выйдя из точки (t0, x0), движется по кривой {t, x(t)}, определяемой решением x(t) = x(t, t0, x0) системы уравнений (1). Движение по этой кривой осуществляется до момента времени t = t1 > t0, в который точка (t, x(t)), встречается с множеством Ft (попадает в точку множества Ft). В момент времени t = t1 точка Pt “мгновенно” перебрасывается оператором At из положения 
в положение 
и движется дальше по кривой {t, x(t)}, которая описывается решением 
системы уравнений (1). Движение по указанной кривой происходит до момента времени t2 > t1, в которой точка Pt снова встречается с множеством Ft. В этот момент под действием оператора At точка Pt мгновенно перескакивает из положения 
в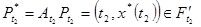 
и движется дальше по кривой {t, x(t)}, описываемой решением 
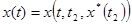системы уравнений (1), до новой встречи с множеством Ft и т.д.
Совокупность соотношений а) – в) называют системой диф. уравнений с импульсным воздействием.
Кривую {t, x(t)} описываемую точкой Pt называют интегральной кривой, а функцию x = x(t), которая задает эту кривую – решением системы (1).
Систему диф. уравнений с импульсным воздействием (совокупность соотношений а)- в)) можно записать в более компактной форме:
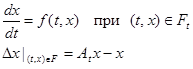(6)
Т.о., решение системы уравнений (2) 
- это функция, удовлетворяющая уравнению (5) вне множества Ft и имеющая разрывы первого рода в точках Ft со скачками
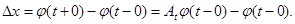
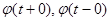- состояние системы до и после скачка в момент времени t1.
В зависимости от характера импульсного воздействия выделяют несколько видов таких уравнений. Рассмотрим систему с нефиксированными моментами импульсного воздействия, т.е. системы, подвергающиеся импульсному воздействию в момент попадания изображающей точки Pt на заданные поверхности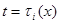 
расширенного фазового пространства. Тогда система (6) примет вид:
(7)