Применимо, в частности, к системам с малым запаздыванием того или иного рода, а также к некоторым системам с сухим трением.
Для каждой точки  пусть
пусть  - наименьшее выпуклое замкнутое множество, содержащее все предельные значения вектор-функции
- наименьшее выпуклое замкнутое множество, содержащее все предельные значения вектор-функции 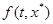 , когда
, когда 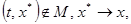
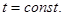 Решением уравнения (1) называется решение включения (2) с только что построенным
Решением уравнения (1) называется решение включения (2) с только что построенным  . Т.к.
. Т.к.  - множество меры нуль, то при почти всех
- множество меры нуль, то при почти всех 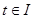 мера сечения множества
мера сечения множества  плоскостью
плоскостью 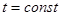 равна нулю. При таких
равна нулю. При таких  множество
множество  определено для всех
определено для всех 
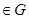 . В точках непрерывности функции
. В точках непрерывности функции  множество
множество  состоит из одной точки
состоит из одной точки 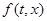 и решение удовлетворяет уравнению (1) в обычном смысле. Если же точка
и решение удовлетворяет уравнению (1) в обычном смысле. Если же точка 
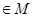 лежит на границах сечений двух или нескольких областей
лежит на границах сечений двух или нескольких областей  , …,
, …, 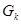 плоскостью
плоскостью 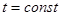 , то множество
, то множество  есть отрезок, выпуклый многоугольник или многогранник с вершинами
есть отрезок, выпуклый многоугольник или многогранник с вершинами 
 ,
,  , где
, где

 =
= 
 .
.
Все точки 
 (
(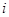 = 1, …,
= 1, …, 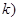 содержатся в
содержатся в  , но не обязательно, чтобы все они являлись вершинами.
, но не обязательно, чтобы все они являлись вершинами.
Определение 3.
Вектор-функция  , определенная на интервале
, определенная на интервале  называется решением уравнения (1), если она абсолютно непрерывна и если при почти всех
называется решением уравнения (1), если она абсолютно непрерывна и если при почти всех  для любого
для любого 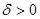 вектор
вектор 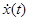 принадлежит наименьшему выпуклому замкнутому множеству (
принадлежит наименьшему выпуклому замкнутому множеству (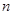 -мерного пространства), содержащему все значения вектор-функции
-мерного пространства), содержащему все значения вектор-функции 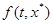 , когда
, когда 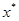 пробегает почти всю
пробегает почти всю  -окрестность точки
-окрестность точки 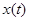 в пространстве X (при фиксированном
в пространстве X (при фиксированном 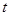 ), т.е. всю окрестность, кроме множества мера нуль.
), т.е. всю окрестность, кроме множества мера нуль.
Такое определение дает однозначное продолжение решения по поверхности разрыва.
Рассмотрим случай, когда функция 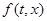 разрывна на гладкой поверхности
разрывна на гладкой поверхности 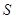 , задаваемой уравнением
, задаваемой уравнением  . Поверхность S делит свою окрестность в пространстве на области
. Поверхность S делит свою окрестность в пространстве на области 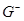 и
и  . Пусть при
. Пусть при 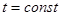 и приближении
и приближении 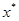 к
к 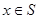 из областей
из областей 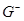 и
и  функция имеет предельные значения
функция имеет предельные значения

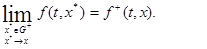
Тогда множество  , о котором говорится в доопределении А, есть отрезок, соединяющий концы векторов
, о котором говорится в доопределении А, есть отрезок, соединяющий концы векторов 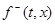 и
и  , проведенных из точки
, проведенных из точки 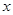 .
.
aЕсли этот отрезок при 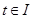 лежит по одну сторону от плоскости
лежит по одну сторону от плоскости  , касательной к поверхности
, касательной к поверхности 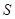 в точке, то решения при этих
в точке, то решения при этих 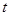 переходят с одной стороны поверхности
переходят с одной стороны поверхности 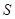 на другую:
на другую:
Рис. 1.
aЕсли этот отрезок пересекается с плоскостью  , то точка пересечения является концом вектора
, то точка пересечения является концом вектора  , определяющего скорость движения
, определяющего скорость движения
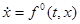 (3)
(3)
по поверхности 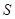 в пространстве
в пространстве  :
:
|
|
|
|
|
|
|
|

Рис. 2.
Причем касательный вектор к S  , следовательно
, следовательно 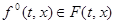 . Это значит, что функция
. Это значит, что функция 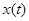 , удовлетворяющая уравнению (3) в силу доопределения А считается решением уравнения (1). Разумеется, непрерывная функция
, удовлетворяющая уравнению (3) в силу доопределения А считается решением уравнения (1). Разумеется, непрерывная функция  , которая на данной части рассматриваемого интервала времени проходит в области
, которая на данной части рассматриваемого интервала времени проходит в области 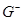 (или в
(или в 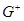 ) и там удовлетворяет уравнению (1), а на оставшейся части проходит по поверхности
) и там удовлетворяет уравнению (1), а на оставшейся части проходит по поверхности 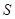 и удовлетворяет уравнению (3), также считается решением уравнения (1) в смысле доопределения А.
и удовлетворяет уравнению (3), также считается решением уравнения (1) в смысле доопределения А.
В уравнение (3) 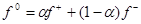 ,
,
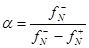 , (
, (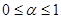 ),
),
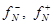 - проекции векторов
- проекции векторов 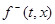 и
и 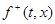 на нормаль к поверхности
на нормаль к поверхности 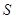 в точке
в точке 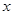 (нормаль направлена в сторону области
(нормаль направлена в сторону области  ).
).
Вместе с тем множество F(t, x) можно было определить иначе. В качестве ) возьмем произвольное ограниченное выпуклое множество, содержащее отрезок J:
|

Рис. 3.
При этом на касательной плоскости появляются векторы, отличные от 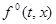 ; это приводит к тому, что кроме решения Филиппова появляются и другие решения.
; это приводит к тому, что кроме решения Филиппова появляются и другие решения.
Т.о. определение (А) А.Ф. Филиппова соответствует минимальному возможному определению множества F(t, x) среди всех допустимых. Это удобно в том отношении, что для решения в смысле Филиппова чаще, чем в других случаях, имеет место единственность решения.
aЕсли весь отрезок с концами 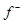 и
и 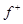 лежит на плоскости P, то скорость движения
лежит на плоскости P, то скорость движения 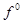 по поверхности разрыва S определяется неоднозначно.
по поверхности разрыва S определяется неоднозначно.
При 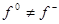 ,
, 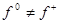 имеет место скользящий режим, о котором шла речь во введение. Пусть уравнение идеального скольжения имеет вид (3). Вычисляя
имеет место скользящий режим, о котором шла речь во введение. Пусть уравнение идеального скольжения имеет вид (3). Вычисляя 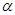 для
для 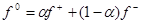 из условия
из условия 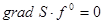 , находим уравнение
, находим уравнение
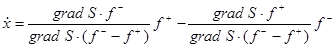 , (4)
, (4)
с помощью котрого и доопределяется движение в скользящем режиме (начальные условия для (4) выбираются на поверхности разрыва, т. е. S(x( 0 ))= 0).
Пример 3.
Решить систему

Всякое решение этой системы рано или поздно попадает на прямую  и уже не может сойти с нее. Если точка М лежит на оси
и уже не может сойти с нее. Если точка М лежит на оси 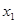 , то в окрестности этой точки вектор
, то в окрестности этой точки вектор 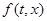 , компоненты которого - правые части системы, принимает два значения:
, компоненты которого - правые части системы, принимает два значения: 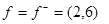 при
при  ,
, 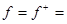 (6,-2) при
(6,-2) при  . Отложим из точки М эти два вектора и соединим их концы отрезком АВ:
. Отложим из точки М эти два вектора и соединим их концы отрезком АВ:

Этот отрезок и будет искомым множеством, в котором, согласно определению 3, лежит конец вектора  для точки М. В то же время вектор скорости
для точки М. В то же время вектор скорости 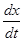 должен лежать на оси
должен лежать на оси 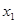 . Т.к. решение не может сойти с нее ни вверх, ни вниз, следовательно, конец вектора лежит в точке пересечения отрезка АВ и оси
. Т.к. решение не может сойти с нее ни вверх, ни вниз, следовательно, конец вектора лежит в точке пересечения отрезка АВ и оси 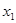 . Т.о., этот вектор определяется однозначно. Легко подсчитать, что
. Т.о., этот вектор определяется однозначно. Легко подсчитать, что 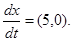
Т.о., связь теорий уравнений (1) с разрывной правой частью с теорией диф. Включений (2) очевидна. Имея уравнение (1) с разрывной f(t, x) необходимо заменить значение  в точке разрыва
в точке разрыва  некоторым множеством. Это множество должно быть ограниченным, выпуклым, замкнутым. Кроме этого оно должно включать все предельные значения
некоторым множеством. Это множество должно быть ограниченным, выпуклым, замкнутым. Кроме этого оно должно включать все предельные значения  при (t, x)
при (t, x)  . После такой замены (для любой точки разрыва) вместо (1) получаем диф. включение (2), в котором многозначная функция
. После такой замены (для любой точки разрыва) вместо (1) получаем диф. включение (2), в котором многозначная функция  удовлетворяет перечисленным требованиям.
удовлетворяет перечисленным требованиям.
Однако, в некоторых случаях множество  в (2) в точках разрыва функции
в (2) в точках разрыва функции 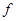 нельзя определить, зная только значения функции
нельзя определить, зная только значения функции 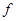 в точках ее непрерывности.
в точках ее непрерывности.
Пример 4.
В механической системе с сухим трением:
 ,
,
 масса тела,
масса тела,  его отклонение,
его отклонение, 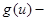 упругая сила,
упругая сила,  сила трения, являющаяся нечетной и разрывной при
сила трения, являющаяся нечетной и разрывной при  =0 функцией скорости
=0 функцией скорости  ,
,  -внешняя сила. Трение покоя
-внешняя сила. Трение покоя 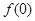 может принимать любые значения между [d1] своим наибольшим и наименьшим значениями
может принимать любые значения между [d1] своим наибольшим и наименьшим значениями 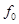 и -
и - 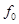 . Если
. Если 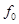 =
= 
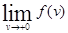 , то применимо доопределение
, то применимо доопределение 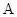 . Если же
. Если же 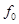 >
> 
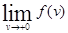 , то движение с нулевой начальной скоростью зависит не только от значений функции в областях ее непрерывности, но и от величины
, то движение с нулевой начальной скоростью зависит не только от значений функции в областях ее непрерывности, но и от величины  . Доопределение А тогда неприменимо. В обоих случаях систему можно записать в виде включения (2). Множество
. Доопределение А тогда неприменимо. В обоих случаях систему можно записать в виде включения (2). Множество 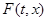 при
при  – точка, а при v =0 – отрезок, длина которого зависит от
– точка, а при v =0 – отрезок, длина которого зависит от  .
.
Следовательно, множество 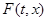 не всегда определяется предельными значениями функции
не всегда определяется предельными значениями функции 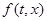 из (1), и в общем случае это множество надо задавать, используя какие-то сведения о рассматриваемой системе.
из (1), и в общем случае это множество надо задавать, используя какие-то сведения о рассматриваемой системе.
Необходимость охватить такие системы приводит к следующему способу построения множества F(t,x).
Рассмотрим систему
 , (6)
, (6)
где 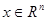 , вектор-функция
, вектор-функция  непрерывна по совокупности аргументов, а скалярные или векторные функции
непрерывна по совокупности аргументов, а скалярные или векторные функции 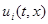 разрывны соответсвенно на множествах
разрывны соответсвенно на множествах 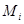 , i=1,…,r, которые могут иметь общие точки и даже совпадать. В каждой точке (t, x) разрыва функции
, i=1,…,r, которые могут иметь общие точки и даже совпадать. В каждой точке (t, x) разрыва функции 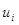 задается замкнутое множество
задается замкнутое множество 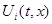 - множество возможных значений аргумента
- множество возможных значений аргумента 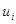 функции
функции 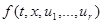 . Предполагается, что при
. Предполагается, что при  аргументы
аргументы 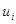 и
и  могут независимо друг от друга пробегать соответственно множества
могут независимо друг от друга пробегать соответственно множества  и
и  . Обычно, это условие выполнено, если функции
. Обычно, это условие выполнено, если функции 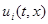 и
и  описывают различные независимые составные части (блоки) физической системы. В точках, где функция
описывают различные независимые составные части (блоки) физической системы. В точках, где функция 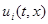 непрерывна, множество
непрерывна, множество 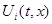 состоит из одной точки
состоит из одной точки 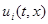 . В точках, разрыва функции
. В точках, разрыва функции  необходимо, чтобы множество
необходимо, чтобы множество  содержало все точки, предельные для точек любой из последовательностей вида
содержало все точки, предельные для точек любой из последовательностей вида 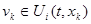 , где
, где  k =1,2,…(или
k =1,2,…(или 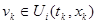 , где
, где 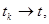
 k =1,2,…). Потребуем, чтобы множество
k =1,2,…). Потребуем, чтобы множество  было выпуклым (если
было выпуклым (если 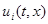 - скалярная функция, то
- скалярная функция, то  - отрезок или точка).
- отрезок или точка).
Пусть
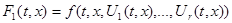 (7) множество значений функции
(7) множество значений функции 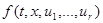 , когда t, x постоянны, а
, когда t, x постоянны, а 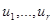 независимо друг от друга пробегают соответственно множества
независимо друг от друга пробегают соответственно множества  .
.
Определение 4.
Решением диф. уравн. (6) называют решение диф. включения (2), где 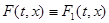 (или
(или  , где
, где 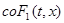 - наименьшее выпуклое множество, содержащее множество
- наименьшее выпуклое множество, содержащее множество 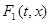 ).
).
Частными случаями такого способа построения функции F(t,x) является как доопределение А, так и изложенные ниже Б и В.