Задание 2.
1. Вставьте в поворотный стол один из исследованных объектов (объект 4 или 5) и установите поворотный стол в начальное положение (нулевая координата).
2. Добейтесь максимальной поляризации света в вертикальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в вертикальное положение.
3. После этого при помощи ручки 1 поворотного стола вращайте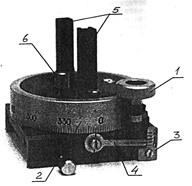
Рис. 12.
Модуль 13 (стол поворотный, рис.12) предназначен для установки объектов с возможностью поворота вокруг вертикальной оси, а также для отсчета угловых координат и углов поворота. Поворот стола производится ручкой 1. Отсчет угловых координат производится по основной шкале 2 (цена деления 20) и нониусу 3 (цена деления 0,50). Рычаг 4 поворачивают до совпадения его вертикальной риски с одним из делений основной шкалы и снимают отсчет по основной шкале. К полученному значению прибавляют отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10, при погрешности порядка 0,20. углы поворота определяют как разности угловых координат. Объекты вставляют в кронштейны 5; винтом 6 регулируют наклон платформы стола и установленного на столе объекта.
Набор объектов
При выполнении лабораторных работ помимо функциональных модулей используется также ряд объектов. Большая часть объектов – тонкие пластины, пленки или линзы, расположенные в средней плоскости соответствующего экрана. При установке экрана в кассету функционального модуля эта плоскость оказывается напротив риски рейтера или иной характерной отметки на модуле. Тем самым определяется координата объекта на оптической скамье.
Объект №1 – сетка с шагом 1 мм, используется для калибров
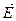не параллельны плоскости падения (горизонтальная плоскость), т. к. поляризатор неидеальный. Найденный угол и будет являться углом Брюстера.
Эксперимент
1. Установка оборудования.
Для проведения работы, необходимо установить на оптической скамье модуль 12, представляющий собой поляризатор с нониусом, модуль 13 – стол поворотный, в который установлена плоскопараллельная пластинка (объект 4)) последовательно друг за другом.
2. Калибровка установки.
После установки приборов необходимо произвести калибровку установки. Сначала при помощи ручки 1 (рис.) поворотного стола устанавливают его на нулевую угловую координату, рычаг 4 поворачивают до совпадения его вертикальной риски с нулевым делением основной шкалы.
Затем двумя передними винтами 6 и двумя задними винтами 2 излучателя (рис.) добиваются совпадение падающего и отраженного света (отраженный свет должен попасть в трубку излучателя).
Так определяется положение нормали к пластинке.
3. Измерения.
Задание 1.
1. Добейтесь максимальной поляризации света в горизонтальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в горизонтальное положение так, чтобы нулевая координата оси поляризатора была напротив риски нониуса.
2. После этого при помощи ручки 1 поворотного стола вращайте
. Вместе с тем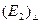 
будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.
Порядок выполнения работы
Для экспериментального определения угла Брюстера пользуются тем, что при некотором значении угла падения от границы раздела двух диэлектриков отразится только электромагнитная волна с такой поляризацией, в которой колебания вектора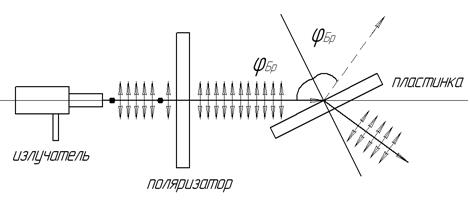 
Рис. 9.6. Схема установки. Колебания вектора 
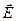в плоскости падения условно обозначены стрелками, колебания, перпендикулярные плоскости пдания – точками.
Так как при прохождении через поляризатор свет полностью
Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света
на границу раздела двух сред под углом Брюстера перпендикулярны.
Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).
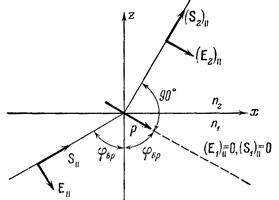Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.
Вектор 
Рис. 1.1.
Доказательством прямолинейности распространения света служит образование тени. От точечного источника света возникает полная тень. Лучи, исходящие из одной точки, образуют расходящийся пучок (сечение пучка увеличивается). Лучи, сходящиеся в одну точку, образуют сходящийся пучок.
При падении световой волны на плоскую границу раздела
. Вместе с тем коэффициент отражения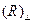 
не обращается в нуль при 
, так как знаменатель выражения (2.4)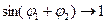 
. Таким образом, получается, что при некотором значении угла падения от границы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора 
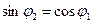и, значит,
.
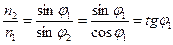Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера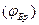 
. В этих обозначениях
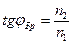. (9.5)
Для перехода световой волны (видимая область спектра) из воздуха в стекло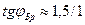 
, что соответствует углу 
.
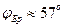Заметим, что отражение полностью поляризованной волны
, где c= 3·108 м/с – скорость света в вакууме, ε – относительная диэлектрическая проницаемость среды, μ – относительная магнитная проницаемость среды (для подавляющего большинства диэлектрических сред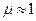 
). Отношение
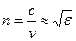(1.1)
называется абсолютным показателем преломления света. Отношение
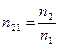(1.2)
называется относительным показателем преломления света средой 2 по отношению к среде 1.
Формулы (1.1), (1.2) справедливы только для волн, частоты которых малы по сравнению с частотой процессов в атомах и молекулах среды. Вследствие дисперсии показателя преломления данные формулы справедливы лишь для монохроматических волн. Среды, в которых распространяются отраженная и преломленная волны, считаются полубесконечными, т.е. принимается, что на границе раздела сходятся только три волны: падающая, отраженная, преломленная, т.е. пренебрегают многократным отражением.
При падении световой волны на идеальную плоскую границу раздела 2-х диэлектриков, размеры которой значительно превышают длину волны, угол между направлением распространения отраженной волны и нормалью к границе раздела ι’1 (угол отражения) равен по абсолютной величине соответствующему углу для падающей волны ι1 (закон отражения, рис.1.1). Угол между направлением распространения преломленной волны и нормалью к границе раздела (угол преломления ι2) связан с углом падения законом преломления света:
.
Отсюда легко получаются искомые зависимости
, 
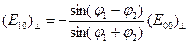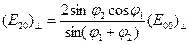. (9.4)
Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения 
от угла падения (рис 9.3).
Рис.9.3. Зависимость коэффициента отражения R от угла падения
При переходе света из воздуха (n1»1) в стекло (n2»1,5).
Рассмотрение формул Френеля показывает, что компоненты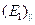 
, и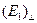 
, по-разному изменяются с увеличением угла 
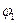. Во-первых, сразу видно, что есл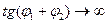и 
и,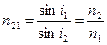
(1.3)
где n21 – относительный показатель преломления среды, в которой распространяется свет, относительно среды в которой распространяется падающий свет.
Если световая волна из оптически более плотной среды 1 падает на границу раздела с оптически менее плотной средой 2 (т.е. если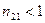 
), то при угле падения i1>iкр где sin iкр = n21, величина sin i2> 1, что невозможно. Угол iкр при котором i2= 900 и преломленная волна отсутствует, называется критическим углом падения света. Явления отражения света целиком в первую среду называется полным внутренним отражением света. Энергия падающей электромагнитной волны полностью возвращается в первую среду, но места захода падающей и выхода отраженной волны на границе раздела смещены друг относительно друга на расстояние порядка половины длины световой волны.
Отношение интенсивности отраженной волны к интенсивности падающей называется коэффициентом отражения света второй среды относительно первой. Отношение интенсивностей преломленной к интенсивности падающей волны называется коэффициентом пропускания второй среды относительно первой.
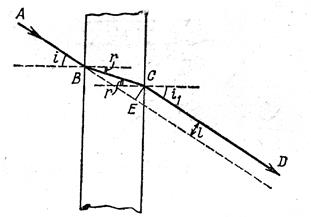Рис. 1.2.
В геометрической оптике каждая точка источника света счита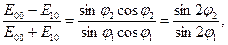
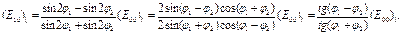(9.2)
Складывая уравнения (2.1), получаем:
,
откуда
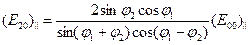. (9.3)
2. Вектор 
, 
и 
согласно рис. 9.2. На нем векторы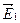 
и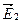 
направлены от читателя перпендикулярно к плоскости чертежа.
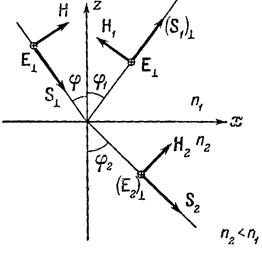Рис. 9.2. Направления векторов 
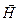на границе раздела.
Вектор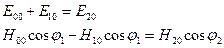 
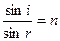, (1.4)
где n – показатель преломления пластинки. Для преломления в точке С закон (1.3) дает:
, (1.5)
так как в этом случае луч выходит из пластинки в воздух. Перемножив выражения (1.4) и (1.5), находим:
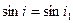, (1.6)
или, так как ι<900 и i1<900, i=i1, откуда следует, что лучи АВ и CD параллельны.
Луч CD смещен в сторону относительно падающего луча АВ. Величина смещения h=EC зависит от толщины пластинки и углов падения и преломления. Смещение, очевидно, тем меньше, чем тоньше пластинка.
Расстояние, на которое смещает пластинка лучи света можно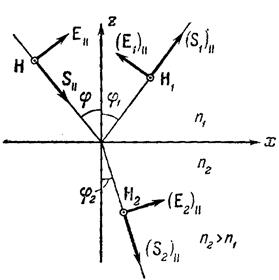
Рис. 9.1.Направления векторов 
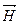имеем:
.
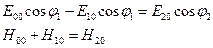Учитывая, что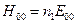 
, 
, 
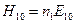, а также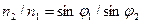 
, находим:
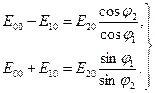(9.1)
Тогда
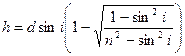, (1.7)
где d – толщина пластинки.
1.3. Преломление света в призме.
Пусть луч АВ падает на одну из граней призмы (рис.1.3), преломившись в точке В, луч пойдет по направлению ВС и, вторично преломившись в точке С, выйдет из призмы воздух. Найдем угол D, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим p. Из четырехугольника BQCN в котором углы при В и С – прямые, найдем, что угол BNC равен 1800- p. Пользуясь этим, из четырехугольника BMCN находим:
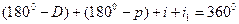, (1.8)
отсюда:
. (1.9)
Угол p, как внешний угол в треугольнике BCN, равен:
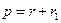, (1.10)
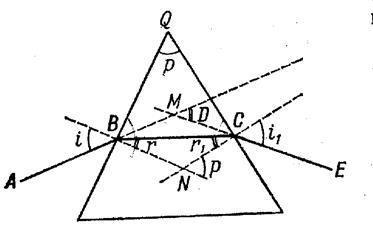Рис. 1.3.
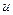, но поляризованных в двух взаимно перпендикулярных направлениях, причем фазы этих двух колебаний никак не скоррелированы. Таким способом можно моделировать хаотическую суперпозицию различных эллиптически поляризованных электромагнитных волн, обусловленную обрывами монохроматических колебаний.
Для каждого момента времени можно вычислить величину суммарной напряженности электрического поля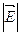 
, если известны две ее проекци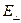и (
и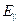 
.) на границу раздела двух диэлектриков, от которой происходит отражение света. В самом деле, 
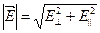. И наоборот, зная 
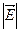, можно разложить его на две взаимно перпендикулярные компоненты. В качестве направлений таких компонент 
, 
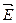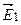и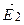 
для какого-то момента времени показаны на рис. 9.1 (
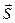- вектор Умова-Пойтинга).
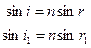. (1.11)
С помощью полученных уравнений, зная преломляющий угол призмы p и показатель преломления n, мы можем при любом угле падения i вычислить угол отклонения D.
Особенно простую форму получает выражения для угла отклонения в том случае, когда преломляющий угол призмы p мал, т.е. когда призма тонкая. А угол падения i невелик; тогда угол i 1 также мал. Заменяя приближенно в формулах (1.11) синусы углов самими углами (в радианах) имеем:
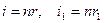. (1.12)
Подставляя эти выражения в формулу (1.9) и пользуясь (1.10), находим:
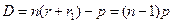(1.13)
Обратите внимание, что угол отклонения луча в призме зависит от показателя преломления вещества, из которого сделана призма. Показатель преломления для разных длин волн различен. Для прозрачных тел показатель преломления фиолетового участка спектра наибольший, затем следует синий участок, зеленый, желтый и наконец наименьший показатель преломления у красного участка спектра. В соответствии с этим, угол отклонения D для фиолетовых лучей наибольший, для красных – наименьший, и луч белого цвета, падающий на призму, на выходе из нее окажется разложенным на ряд цветных лучей, т.е. образуется спектр, данное явление носит название дисперсии.
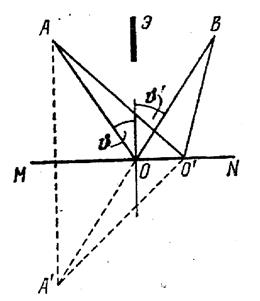Рис. 1.4.
1.4. Принцип Ферма.
В основу геометрической оптики может быть положен принцип, установленный французским математиком Ферма. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света. В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.
Для прохождения участка пути ds (рис.1.4), свету требуется время dt=ds/v, где v – скорость света в данной точке среды. Считая что v=c/n, получим dt=(1/c)nds. Следовательно время τ, затрачиваемое светом на прохождение пути от точки 1 до точки 2 равно:
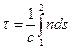(1.14)
Имеющая размерность длины величина
, 
.
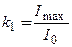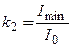6. Определите по формуле (8.4) степень поляризации неидеального поляризатора.
7. Результаты занесите в таблицу:
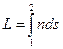(1.15)
называется оптической длиной пути. В однородной среде оптическая длина равна произведению геометрической длины пути s на показатель преломления среды n:
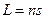. (1.15а)
Согласно (1.14):
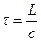. (1.14а)
Пропорциональность времени прохождения τ оптической длине пути L дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, либо стационарной – одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохроными (требующими для своего прохождения одинакового времени).
Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется минимален в случае распространения света в обратном направлении. Следовательно, луч, пущенный навстречу лучу, проделавшему путь от точки 1 до точки 2. пойдет по тому же пути, но в обратном направлении. Получим при помощи принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В отразившись от поверхности MN (рис.1.4). Среда в которой проходит луч однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Геометрическая длина произвольно взятого пути равна АО’В=A’O’B (вспомогательная точка А’ является зеркальным отображением точки А). Из рисунка 1.4 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. Заметим, что при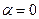
).
4. Изменяя относительный угол между поляризатором и анализатором измеряйте показания мультиметра, добейтесь минимального и максимального значения, показания заносите в таблицу через каждые 30 – 50 (в пределах от 0 до 900):
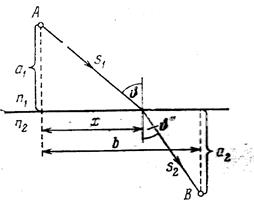Рис. 1.5.
Теперь найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была экстремальна (рис.1.5), для произвольного луча оптическая длин пути: