Эксперимент
1. Для объекта 27, используя то же оборудование, при максимальном (допускаемом установкой) значении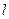
измерьте ширину интерференционной полосы. Для этого разность координат минимумов, разнесенных на несколько полос в пределах центрального дифракционного максимума, разделите на число полос. На рис.4.5 показано
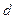, то расходящийся дифракционный пучок наблюдается на фоне незакрытого «прямого пучка».
Длина дифракции
Вследствие дифракционной расходимости размер освещенной области на экране Э2 будет превышать начальные размеры пучка 
. (6.2)
Если 
, размер пятна практически равен 
, на котором дифракционное уширение становится сравнимым с начальным размером пучка, называют длиной дифракции. Из условия 
находим:
. (6.3)
Если выполняется записанное в различных формах условие
, 
, 
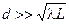, (6.4)
то работает геометрическая оптика. Если же
, 
, 
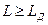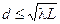, (6.5)
то существенно явление дифракции. При 
размер пятна 
, и распределение интенсивности полностью определяется дифракцией.
Характер распределения интенсивности в дифракционной картине зависит от отношения длины дифракции 
, где 
и 
- координаты центров двух темных полос, симметричных относительно центрального максимума, 
- число светлых полос между двумя данными темными, 
- увеличение микропроектора (на рис. 4.5 N = 3).
Рис. 4.5.
2. Выньте объект 27 из двухкоординатного держателя и вставьте его в кассету микропроектора (модуль 2). Отодвиньте объектив на 1,5 – 2 см ближе к конденсору (модуль 5), при этом система расфокусируется, объект 27 в кассете микропроектора окажется освещенным, и на экране установки будет видно увеличенное изображение двух щелей. Измерьте по этому изображению ширину щели D и расстояние между щелями Н. Учитывая увеличение микропроектора, рассчитайте действительную ширину щели 
и расстояние между щелями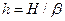 
.
3. Рассчитайте длину волны излучения лазера по формуле: 
.
4. Повторите опыт с объектом 28.
5. Результаты занесите в таблицу:
можно считать бесконечно малой величиной. Чем хуже выполнено это условие, тем сильнее проявляются отклонения от законов геометрической оптики, приводящие к возникновению явлений дифракции. По законам геометрической оптики за краем непрозрачного экрана должна находится область тени (геометрическая тень), резко ограниченная от освещенных областей и соответствующая профилю края экрана. Вследствие дифракции вместо этого получается сложное распределение интенсивности, называемое дифракционной картиной.
Угол дифракции
Рис. 6.1.
Пусть отверстие в экране Э1 «вырезает» пучок из плоской монохроматической волны (рис. 6.1), и след пучка наблюдается на экране Э2. Уменьшая размер отверстия, заметим, что вначале размер следа пучка уменьшается в соответствии с размером отверстия, но затем начинает увеличиваться: пучок становится расходящимся. Угловая ширина пучка (угол дифракции 
) определяется соотношением между длиной волны 
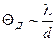. (6.1)
Соотношение (6.1.) позволяет оценить порядки дифракционных