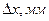Пучок излучения лазера превращается собирающей линзой в сферическую волну, вначале сходящуюся к фокусу, а после фокуса – расходящуюся. Требуется проследить характер изменения интенсивности с координатой -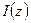 
. В качестве 
используются показания вольтметра без пересчета в абсолютные значения.
Эксперимент
1. Снимите с излучателя рассеивающую линзу-насадку. В конце свободной скамьи установите микропроектор (модуль 2) и, вплотную перед ним линзу-конденсор (модуль 5). Убедитесь в том, что при отодвигании модуля 5 от модуля 2 изменяется размер пятна на экране установки и интенсивность излучения в центре пятна. Верните конденсор в начальное положение.
2. Поместите в объектную плоскость микропроектора фотодатчик – объект 38, подключите фотодатчик к мультиметру, мультиметр поставьте в режим измерения постоянного напряжения (диапазон измерений – до 1 В) и снимите зависимость напряжения на вольтметре от координаты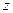 
модуля 5 с шагом 10 мм, принимая за точку отсчета координату риски модуля 2. Сделайте 20 измерений.
3. Постройте график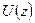 
. Качественно он аналогичен графику .
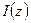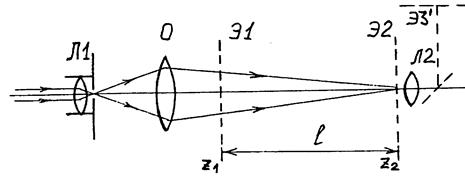Рис. 6.6.
5. Медленно отодвигая микропроектор от объекта, наблюдайте за поведением тени диска. Определите, на каком расстоянии от диска в центре тени станет заметно светлое пятно. Соответствует ли это расстояние условию наблюдения дифракции (6.5)?
Задание 2. Дифракция Френеля на круглом отверстии.
Зоны Френеля.
В соответствии с принципом Гюйгенса-Френеля волновое поле на экране Э2 (рис. 6.7) рассматривается как результат суперпозиции волн, испущенных «вторичными» источниками, расположенными, например, в плоскости экрана Э1 и когерентными с полем падающей волны.
и постройте график 
. Интенсивность в данной точке обратно пропорциональна квадрату расстояния до центра волны: 
. Значит, 
. Поэтому зависимость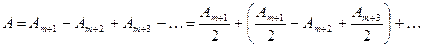 
(6.19)
или
, (6.20)
так как выражения, стоящие в скобках в формуле (6.19), согласно (6.15), равны нулю. Следовательно, в точке Р всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах (светлых кольцах) убывает с расстоянием от центра картины.
С увеличением радиуса диска первая открытая зона Френеля удаляется от точки Р и увеличивается угол между нормалью к поверхности зоны и направлением на точку Р. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весома слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.
Порядок выполнения работы
Задание 1. Наблюдение дифракции Френеля на диске.
Вследствие дифракции свет попадает в область геометрической тени. Предсказанное волновой теорией дифракции Френеля световое пятно в центре тени круглого экрана («пятно Пуассона») послужило триумфу этой теории.
Эксперимент
1. Отъюстируйте установку по методике на стр. 12.
2. На свободную оптическую скамью установите, как показано на рис.6.6, линзу-конденсор Л1 (модуль 5) вплотную к излучателю, двухкоординатный держатель с объектной плоскостью Э1 (модуль 8) на расстоянии 25 – 30 см от конденсора, объектив О (модуль 6) между модулями 5 и 8 на расстоянии около 10 см от модуля 8, микропроектор Л2 (модуль 2) за модулем 8 вблизи от него.
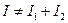. (4.1)
Если разность фаз складываемых колебаний постоянна во времени и равна δ, то 
. Если δ=2kπ (k – целое), то интенсивность максимальна, если δ=(2k+1)π – минимальна. Соответствующие интенсивности равны
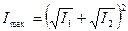, (4.2)
(4.3)
Если I1=I2, то в минимуме Imin=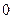 
– свет плюс свет дает темноту. Как правило, в разных точках пространства величина δ имеет разные значения, и возникает чередование темных и светлых полос, называемое интерференционной картиной. Расстояние между соседними светлыми или соседними темными полосами (т.е. между соседними максимумами или минимумами интенсивности) называют шириной интерференционной полосы.
Разность фаз δ определяется оптической разностью хода Δ:
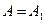, т.е. вдвое больше (интенсивность в четыре раза больше), чем в отсутствие непрозрачной преграды с отверстием. Если отверстие открывает две зоны Френеля, то их действия в точке Р практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки Р будет иметь вид чередующихся темных и светлых колец с центрами в точке Р, причем если m нечетное, то в центре будет светлое пятно (соответствующее распределение интенсивности света показано на рис. 6.4 б), если m четное, то в центре будет темное пятно (рис. 6.4 в).
Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то 
и результирующая амплитуда 
, т.е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины в этом случае наблюдаться не будет, свет распространяется прямолинейно, как и в отсутствии непрозрачной преграды.
2. Дифракция на диске. Пусть сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционная картина наблюдается на экране в точке Р, лежащей на линии, соединяющей S c центром диска (рис. 6.5). В данном случае закрытый диском участок волнового фронта надо исключить
, где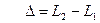 
, (4.4)
L2 и L1 – «оптические длины» 2-х лучей, идущих от источника до точки наблюдения, 
– длина волны излучения в вакууме. Отрезку луча длиной l в среде с показателем преломления n соответствует оптическая длина L=nl. Для луча, прошедшего от точки A до тоски B:
. (4.5)
Условия интерференционного максимума и минимума:
max: 
, k – целое, (4.6)
min: 
, k – целое, (4.7)
где λ0 – длина волны излучения в вакууме.
В общем случае можно записать:
. (4.8)
Параметр 
называют порядком интерференции. Целым 
. (6.17)
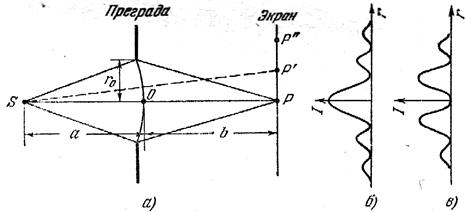Рис. 6.4.
При величинах a и b порядка метров радиус центральной зоны Френеля, рассчитанный по формуле (6.17) будет иметь порядок миллиметров.
6.3. Дифракция Френеля на круглом отверстии и диске.
1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути преграду с круглым отверстием (рис. 6.4 а). Дифракционную картину наблюдаем на экране в точке Р, лежащей на линии, соединяющей S и центр отверстия О. Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего светового колебания, возбуждаемого в точке Р всеми зонами, учитывая (6.8) и (6.16), будет равна
, (6.18)
где знак плюс соответствует нечетным m, минус – четным m.
Когда отверстие открывает нечетное число зон Френеля, то
Рис. 4.1.
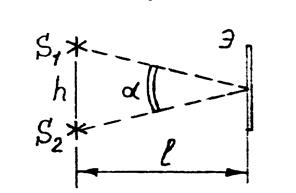Рис. 4.2.
Две плоские волны с малым углом 
между направлениями распространения, в плоскости, перпендикулярной среднему направлению распространения, дают интерференционную картину (рис. 4.1) в виде чередующихся темных и светлых полос. Ширина полосы (расстояние между соседними минимумами или соседними максимумами):
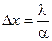. (4.9)
Волны, пришедшие на экран Э от достаточно удаленных точеч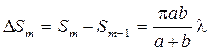
. (6.13)
Выражение (6.13) не зависит от m, следовательно, при не слишком больших m площади зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны.
Согласно предположению Френеля, действие отдельных зон в точке Р тем меньше, чем больше угол между нормалью к поверхности зоны и направлением от зоны на Р, т.е. действие зон постепенно убывает от центральной (около точки О) к периферическим. Кроме того, интенсивность излучения в направлении точки Р уменьшается с ростом m и вследствие увеличения расстояния от зоны до точки Р. Учитывая оба этих фатора, можно записать
А1 > A2 > A3 > …. (6.14)
Общее число зон Френеля, умещающихся на полусфере, очень велико, поэтому в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.
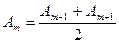. (6.15)
Тогда выражение (6.8) можно записать в виде
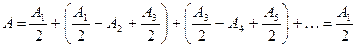, (6.16)
так как выражения, стоящие в скобках, согласно (6.15), равны нулю, а оставшаяся часть от амплитуды последней зоны 
ничтожно мала.
Таким образом, амплитуда результирующих колебаний в произвольной точке Р определяется как бы действием только половины центральной зоны.
Если в выражении (6.10) положим, что высота сегмента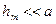 
(при не слишком больших m), тогда 
. Подставив сюда значение высоты сферического сегмента (6.11), найдем радиус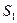
и 
(рис. 4.2), можно в области экрана Э считать плоскими. Очевидно,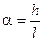 
, где h –расстояние между точечными источниками, l – расстояние от плоскости источников до экрана (
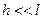), соответственно
. (4.10)
4.2. Опыт Юнга.
В качестве источников используются две щели, освещаемые излучением лазера. Вследствие дифракции пучки излучения после щелей получаются расходящимися, благодаря чему перекрываются и дают интерференционную картину (рис. 4.3а). Однако, при освещении щелей плоской волной, пучки не успевают пересечься в пределах длины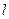 
нашей установки.
Рис. 4.3.
Поэтому мы освещаем щели сходящейся волной (рис. 4.3.б), полученной с помощью короткофокусной линзы и объектива.
Схема опыта приведена на рис. 4.4. Пучок лазера превращается конденсором Л1 и объективом О в волну, сфокусированную в объектной плоскости Э2 линзы Л2 микропроектора с координатой риски 
. При этом на экране установки Э3 видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой 
. При этом в плоскости Э2 образуется интерференционная или ди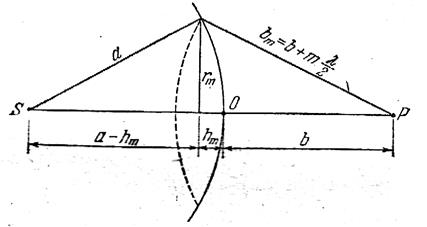
Рис. 6.3.
Для оценки амплитуд колебаний найдем площади зон Френеля. Внешняя граница m -й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис.6.3). Обозначим площадь сегмента через Sm. Тогда площадь m- й зоны можно представить в виде:
, (6.9)
где Sm-1 – площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны. Из рисунка 6.3 следует, что
. (6.10)
После элементарных преобразований, учитывая, что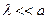 
и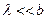 
, из (6.10) получим высоту сферического сегмента:
. (6.11)
Площадь сферического сегмента:
. (6.12)
Площадь m -й зоны:
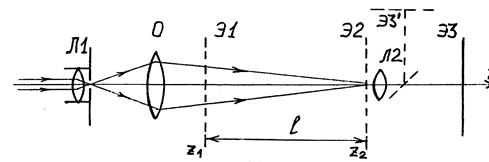Рис. 4.4.
В схеме на рис. 4.4 и последующих вместо реального положения экрана Э3`, показанного пунктиром, дается положение Э3, в котором игнорируется излом лучей зеркалом микропроектора.
Задание 1. Изучение интерференции.
Эксперимент
1. Отъюстируйте установку по методике, описанной на стр. 12.
2. На оптическую скамью последовательно, считая от лазера, установить друг за другом конденсор (модуль 5), объектив (модуль 6) и микропроектор (модуль 2). Конденсор расположите вплотную к излучателю. При положении риски микропроектора 
, (6.7)
где b – расстояние от вершины волновой поверхности О до точки наблюдения. Так как колебания от соседних зон проходят до точки Р расстояния, отличающиеся на λ/2, то в точку Р они приходят в противоположной фазе, и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке Р
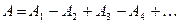(6.8)
где А1, А2, … - амплитуды колебаний, возбуждаемых 1-й, 2-й, …, m-й зонами.
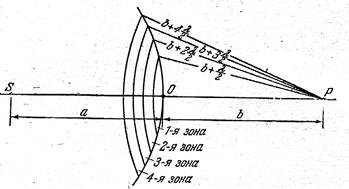Рис. 6.2.
– объект 23. Вместо яркой точки на экране появится пятно, размазанное в направлении, перпендикулярном щели. Оно состоит из центрального дифракционного максимума и ряда побочных максимумов по обе стороны от центрального. Размер пятна определяется фундаментальным соотношением дифракции: если излучение с длиной волны 
проходит через отверстие размером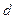 
, то возникает дифракционная расходимость, определяемая углом дифракции 
, порядок величины которого
. (4.11)
Проверьте это соотношение, определив размер центрального максимума. Не забудьте учесть увеличение микропроектора β = 18, т.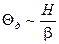е. 
, где 
- размер центрального максимума, 
- увеличение микропроектора. Длину волны принять равной 0,65 мкм. Знак «~» означает, что порядок величин совпадает, т. е. отличие между ними не более, чем в 10 раз.
4. Проведите аналогичное измерение с объектом 24 – щелью шириной 
.
5. Результаты занесите в таблицу:
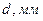
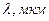
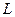до плоскости наблюдения, т. е. от безразмерного параметра дифракции
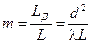. (6.6)
Дифракция Френеля и дифракция Фраунгофера
Если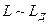 
, то наблюдается наиболее сложный для анализа вид дифракции, называемый дифракцией Френеля. Если 
, то распределение интенсивности на экране Э2 и его расчет упрощаются. Лучи, идущие от экрана Э1 в произвольную точку Р экрана Э2, почти параллельны, а приходящие в точку Р волны – плоские. Такой вид дифракции называют дифракцией Фраунгофера (дифракция в параллельных лучах или дифракция плоских волн).
Область за экраном Э1 можно разбить на три участка:
1) 
, 
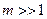- область геометрической оптики;
2) 
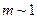- дифракция Френеля (ближняя зона дифракции);
3) 
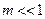- дифракция Фраунгофера (дальняя зона дифракции).
6.2. Дифракция Френеля.
Рассмотрим подробнее дифракцию в ближней зоне.
В основе объяснения дифракционных явлений лежит принцип Гюйгенса – Френеля: световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции (наложения) когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и
. Для этого необходимо зафиксировать 5 значений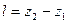 
), измеряя каждый раз 
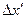по шкале экрана установки, выбрав какую-либо одну полосу (
, шаг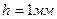 
).
8. Повторите опыт с объектом 28 (
).
9. Результаты занесите в таблицы:
