Лекция 3 Восстановление дискретного сигнала
Наша цель - найти необходимые условия, при которых сигнал может быть восстановлен по дискретной выборке
Прежде всего, отметим часто часто используемый факт: 
Преобразование Фурье от последовательности
Пусть имеется сигнал  , и выбран шаг дискретизации
, и выбран шаг дискретизации 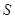 . Функция заменяется последовательностью
. Функция заменяется последовательностью 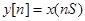 .
.
Определение. Преобразованием Фурье от последовательности называется функция
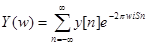 (1)
(1)
Отметим, что функция  является периодической. Часто ради простоты обозначений полагают
является периодической. Часто ради простоты обозначений полагают 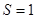 , и в этом случае период функции равен 1. Это принципиальное различие между преобразованиями Фурье от функции и последовательности. В то же время, оба преобразования тесно связаны. Положим
, и в этом случае период функции равен 1. Это принципиальное различие между преобразованиями Фурье от функции и последовательности. В то же время, оба преобразования тесно связаны. Положим  . Тогда
. Тогда
 , (2)
, (2)
то есть является преобразованием Фурье от произведения двух функций, из которых одна - обобщенная функция. Согласно общей теории, преобразование Фурье от произведения двух функций равно свертке образов сомножителей. Здесь мы отступаем от строгого изложения, поскольку уже справедливость (2) требует обоснования. Для упрощения обозначений положим 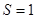 . Найдем
. Найдем 
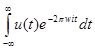 . Снова положим
. Снова положим  =
=
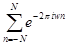 . Обратим внимание на то, что это периодическая функция с периодом 1, представленная суммой геометрической прогрессии. Имеем:
. Обратим внимание на то, что это периодическая функция с периодом 1, представленная суммой геометрической прогрессии. Имеем:
 . Умножим числитель и знаменатель на
. Умножим числитель и знаменатель на  . Получим
. Получим 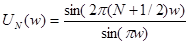 В окрестности 0
В окрестности 0 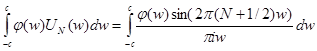 . стремятся при
. стремятся при 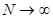 к
к
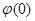 . Таким образом, в окрестности 0
. Таким образом, в окрестности 0  . В силу периодичности, имеем окончательный результат:
. В силу периодичности, имеем окончательный результат: 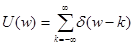 . Для произвольного
. Для произвольного 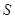 можем написать формулу
можем написать формулу
 (3)
(3)
Связь между непрерывным и дискретным преобразованиями Фурье. Частота Найквиста.
Используя формулы (2) и (3) и, предполагая верным утверждение о преобразовании Фурье от произведения функций, получаем:
 , где
, где  , откуда вытекает
, откуда вытекает
 (4)
(4)
Эта формула устанавливает связь между непрерывным и дискретным преобразованиями Фурье. Как и следовало ожидать,  имеет период
имеет период 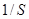 , что согласуется с (1).
, что согласуется с (1).
Предположим, что спектр исходного сигнала ограничен: 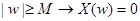 для некоторого
для некоторого  . Выберем
. Выберем 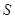 таким образом, чтобы выполнялось неравенство
таким образом, чтобы выполнялось неравенство
 (5)
(5)
В этом случае функция 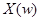 однозначно определяется функцией
однозначно определяется функцией  . Значение
. Значение  называется частотой выборки Найквиста. Если частота выборки больше указанной величины, спектр непрерывного сигнала может быть восстановлен по спектру дискретного. Позже будет показано, что и сам непрерывный сигнал восстанавливается по дискретному.
называется частотой выборки Найквиста. Если частота выборки больше указанной величины, спектр непрерывного сигнала может быть восстановлен по спектру дискретного. Позже будет показано, что и сам непрерывный сигнал восстанавливается по дискретному.
Теорема Котельникова-Шеннона
Эта теорема уточняет результат предыдущего пункта.
Если исходный сигнал имеет ограниченный спектр и выполнено условие (5), то непрерывный сигнал можно восстановить по дискретному.
Доказательство. Пусть спектр сигнала находится в интервале  . Выберем произвольное
. Выберем произвольное 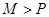 . Тогда
. Тогда  . Функцию, заданную на конечном интервале, можно разложить в ряд Фурье:
. Функцию, заданную на конечном интервале, можно разложить в ряд Фурье:  , где
, где  . Отсюда следует, что
. Отсюда следует, что 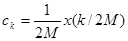 . Теперь
. Теперь  . Положив
. Положив  . Получим
. Получим
 . (6)
. (6)
Замечание. Обратим внимание, что в (5) должно выполняться строгое неравенство, если мы хотим, чтобы утверждение оставалось верным и для сигналов с преобразованием Фурье в виде обобщенной функции. В качестве примера рассмотрим  . Спектр сигнала сосредоточен на интервале
. Спектр сигнала сосредоточен на интервале 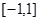 . Положим
. Положим  , тогда
, тогда 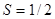 , но последовательность
, но последовательность 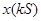 оказывается нулевой. То есть непрерывный сигнал не удается восстановить по дискретным значениям. Если же
оказывается нулевой. То есть непрерывный сигнал не удается восстановить по дискретным значениям. Если же  , то можно воспользоваться формулой (6).
, то можно воспользоваться формулой (6).
Рекомендуемая литература:
1. Глинченко, А. С. Цифровая обработка сигналов: курс лекций. – Красноярск: СФУ, 2008.
2. Глинченко, А. С. Цифровая обработка сигналов: уч. пособие. – 2-е изд., перераб. и доп. – Красноярск: ИПЦ КГТУ, 2005. – 482 с.
3. Глинченко, А. С. Лабораторный практикум по цифровой обработке сигналов: учеб. пособие. – Красноярск: СФУ, 2008.
6. Глинченко, А. С., Голенок А. И. Принципы организации и программирования сигнальных процессоров семейства ADSP-21XX: учеб.-метод. пособие. – Красноярск: ИПЦ КГТУ, 2000. – 88 с.
7. Сергиенко А. Б. Цифровая обработка сигналов: учеб. пособие. – 2-е изд. – СПб.: Питер, 2006. – 751 с.
8. Основы цифровой обработки сигналов: Курс лекций /
А. И. Солонина, Д. А. Улахович., С. М. Арбузов, Е. Б. Соловьева. – СПб.: БХВ-Петербург, 2005. – 768с.