Для глубокого исследования взаимосвязи социально-экономических явлений используется корреляционно-регрессионный анализ. Цель корреляционно-регрессионный анализа – установить, с каким из показателей, включённых в группировку, наиболее тесно связан группировочный признак.
Наметим показатели, которые будут включены в анализ при простой корреляции. Факторный признак – удой молока от 1 коровы, результативный – окупаемость затрат.
Таблица 5
Исходные данные корреляционно – регрессионного анализа
| №№ предприятий | Производительность коров, ц Х | Окупаемость, % Y |
| 22,0 | 107,5 | |
| 23,2 | 110,1 | |
| 21,9 | 95,9 | |
| 28,1 | 93,4 | |
| 23,2 | 81,2 | |
| 26,1 | 106,9 | |
| 21,1 | 97,8 | |
| 22,8 | 94,4 | |
| 23,4 | 85,0 | |
| 22,8 | 86,3 | |
| Итого | 234,5 | 958,5 |
| Ср. знач. | 23,5 | 95,9 |
Установим форму связи между фактором и результатом. Для этого изобразим следующий рисунок.
Рис. 3. Зависимость между удоем молока от 1 коровы и окупаемостью затрат по предприятиям
Исходные данные показывают, что между удоем молока от 1 коровы и окупаемость затрат имеется в основном прямо пропорциональная зависимость, поэтому форму связи определим как линейную.
Подготовим данные для корреляционно – регрессионного анализа
Таблица 6
Расчетные данные корреляционно – регрессионного анализа
| №№ предприятий | Производительность коров, ц Х | Окупаемость, % Y | X*X | Y*Y | X*Y |
| 22,0 | 107,5 | 484,0 | 11551,2 | 2364,5 | |
| 23,2 | 110,1 | 539,5 | 12120,5 | 2557,2 | |
| 21,9 | 95,9 | 478,7 | 9198,3 | 2098,5 | |
| 28,1 | 93,4 | 789,5 | 8731,3 | 2625,5 | |
| 23,2 | 81,2 | 536,7 | 6590,9 | 1880,8 | |
| 26,1 | 106,9 | 678,8 | 11434,0 | 2786,0 | |
| 21,1 | 97,8 | 446,4 | 9567,1 | 2066,5 | |
| 22,8 | 94,4 | 518,8 | 8902,8 | 2149,1 | |
| 23,4 | 85,0 | 545,4 | 7219,4 | 1984,3 | |
| 22,8 | 86,3 | 521,4 | 7455,4 | 1971,5 | |
| Итого | 234,5 | 958,5 | 5539,1 | 92771,1 | 22483,8 |
| Ср. знач. | 23,5 | 95,9 | 553,9 | 9277,1 | 2248,4 |
Определим тесноту связи между изучаемыми признаками, рассчитаем коэффициент корреляции.
σx =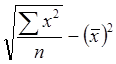 
; σx = 1,98;
σy =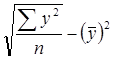 
; σy = 9,47
r =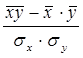 
; r = 0,027; D = 0,07%
Построим уравнение регрессии и определим параметры уравнения: y = a0 + a1x
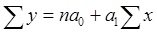-55.93=10*a0+224.96*a1 a0= 92,84
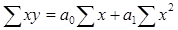-401.61=224.96*a0+5178.37*a1 a1= 0,13
y=0,13*x+92,84
Э1 =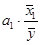 
; Э1= 22,75
Коэффициенты эластичности позволяют сказать следующее: при увеличении удоя молока на 1% окупаемость уменьшается на 22,75 пункта.
Проведенный нами расчет коэффициента корреляции показал, что между производительностью коров и окупаемостью затрат есть связь прямая, так как r – положительное число и слабая корреляционная зависимость (r < 0,3). Коэффициент детерминации равный 0,07 % говорит о том, что в семи случаях из 10000 на изменение окупаемости повлияла продуктивность коров в данных конкретных условиях, во всех других случаях на изменение окупаемости оказали влияние другие неучтенные факторы.
Корреляционное уравнение связи между удоем молока от одной коровы и окупаемостью затрат показывает, что окупаемостью затрат изменяется в среднем на 0,13 % при повышении удоя молока на 1ц.
Показатель окупаемостью затрат связан не с одним, а с несколькими факторами, поэтому следует применить множественный корреляционный анализ. При отборе факторов в математическую модель следует иметь в виду, что нецелесообразно включать в уравнение признаки, которые связаны друг с другом функционально или соотносятся как часть или целое. В уравнение связи должны быть включены факторы, оказывающие непосредственное влияние на результат.
В качестве второго факторного признак возьмём трудоемкость 1ц продукции, чел.-час.
Подготовим данные для множественного корреляционно-регрессивного анализа (таблица 7).
Таблица 7
Исходные данные для множественного корреляционно-регрессионнго анализа
| №№ предприятий | Производительность коров, ц Х1 | Трудоемкость 1ц, чел.-час. Х2 | Окупаемость, % У | X1*X1 | X2*X2 | Y*Y | X1*X2 | X1*Y | X2*Y |
| 22,0 | 9,8 | 107,48 | 96,83 | 11551,2 | 216,4835 | 2364,5 | 1057,6 | ||
| 23,2 | 9,2 | 110,09 | 539,5062 | 84,60 | 12120,5 | 213,6364 | 2557,2 | 1012,6 | |
| 21,9 | 9,6 | 95,908 | 478,7494 | 91,59 | 9198,3 | 209,4017 | 2098,5 | 917,9 | |
| 28,1 | 10,2 | 93,441 | 789,4608 | 104,78 | 8731,3 | 287,6106 | 2625,5 | 956,5 | |
| 23,2 | 9,3 | 81,185 | 536,6944 | 86,08 | 6590,9 | 214,9425 | 1880,8 | 753,2 | |
| 26,1 | 8,2 | 106,93 | 678,8137 | 67,16 | 11434,0 | 213,5135 | 2786,0 | 876,3 | |
| 21,1 | 11,5 | 97,812 | 446,378 | 131,80 | 9567,1 | 242,5532 | 2066,5 | 1122,9 | |
| 22,8 | 11,3 | 94,355 | 518,7606 | 126,90 | 8902,8 | 256,5789 | 2149,1 | 1062,9 | |
| 23,4 | 11,0 | 84,967 | 545,3934 | 120,25 | 7219,4 | 256,0976 | 1984,3 | 931,8 | |
| 22,8 | 12,4 | 86,345 | 521,3611 | 154,88 | 7455,4 | 284,1667 | 1971,5 | 1074,6 | |
| Итого | 234,5 | 102,5 | 958,5 | 1064,88 | 92771,1 | 22483,8 | 9766,2 | ||
| Ср. знач. | 23,5 | 10,2 | 95,9 | 106,49 | 9277,1 | 2248,4 | 976,6 |
Установив перечень признаков-факторов можно записать соответствующее математическое уравнение теоретической линии множественной регрессии. В случае двухфакторной линейной регрессии уравнение связи имеет вид: Y = a0+a0 x1+a2 x2
Рассчитаем парные и частные коэффициенты корреляции и на их основе совокупный коэффициент корреляции.
σy =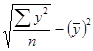 
; σx1 = 
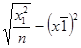; σx2 = 
;
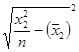σy = 9,47; σx1 = 1,98; σx2 = 9,47
r yx1 =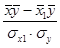 
; r yx1 = 0,027;
r yx2 =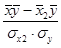 
; r yx2 = -0,487
r x1x2 =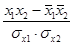 
; r x1x2 = -0,341
r yx1(x2) =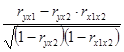 
; ryx1(x2) = -0,18;
r yx2(x1) =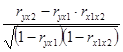 
; r yx2(x1) = - 0,54;
r x1x2(y) =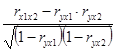 
; r x1x2(y) = -0,375
R yx1x2 =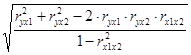 
; R yx1x2 = 0,51.
Определим параметры уравнения множественной регрессии.
а1=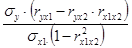 
; a1 = -0,75;
а2=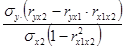 
; a2 = -4,21
а0 =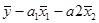 
; a0 = 156,56;
Y = 156,56 – 0,75*x1 –4,21*x2
Определим коэффициенты эластичности:
Э1 =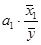 
; Э1= -0,184
Э2=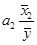 
Э2= - 0,45.
Парные коэффициенты корреляции измеряют тесноту связи между 2-мя признаками из рассматриваемых без учёта взаимодействия их с другими признаками.
На этом основании можно сказать, что связь тесная и обратная по направлению возникает между результативным и факторным признаком х2 – трудоемкостью 1 ц молока, то есть при увеличении факторного признака результативный уменьшается (ryx2 = -0,487). Связь между результативным признаком и фактором х1 – удоем молока от 1 коровы – можно оценить как слабую и прямую (ryx1 = 0.027). Связь между факторными признаками умереная и обратная.
Частные коэффициенты корреляции – характеризуют степень и влияние одного из признаков на другой при условии, что остальные переменные закреплены на постоянном уровне. Рассчитанные показатели вновь подтверждают, что наиболее тесная связь между х2 и у.
Совокупный коэффициент корреляции R yx1x2, характеризующий одновременное влияние факторных признаков на результативный, показывает, что связь между признаками сильная.
Коэффициенты эластичности позволяют сказать следующее: при увеличении удоя молока на 1% окупаемость уменьшается на 0,18 пункта, в то время как увеличение трудоемкости на 1% влечёт уменьшение окупаемости на 0,45 пункта.
Таки образом результативный признак наиболее тесно связан с фактором х2- трудоемкостью.
Индексный анализ продуктивности коров
Для анализа совокупности применим индексный метод. Под индексом в широком смысле понимается относительный показатель, который характеризует соотношение уровней социально-экономического явления во времени, по сравнению с планом и в пространстве.
С помощью индексного анализа необходимо установить изменение исследуемого явления в отчётном периоде по сравнению с базисным и влияние факторов на это изменение. В качестве факторов, влияющих на продуктивность, возьмём средний надой от 1 коровы и поголовье.
Исчислим индексы продуктивности переменного и постоянного составов. Для этого построим таблицу.
Таблица 9
Вспомогательная таблица для расчёта индексов
| №№ предприятий поооп | Поголовье коров | Продуктивность 1 коровы, ц | Валовой надой молока, ц | S1*Y0 | |||
| базисный год | отчетный год | базисный год | отчетный год | базисный год | отчетный год | ||
| S0 | S1 | Y0 | Y1 | Y0*S0 | Y1*S1 | ||
| Предприятие №1 | 22,00 | 21,85 | |||||
| Предприятие №2 | 23,23 | 22,83 | 2810,5 | ||||
| Итого | Х | Х | 5824,5 |
Относительное изменение валового надоя:
IВС =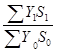 
=0,63;
Iпер сост =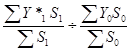 
= 
= 
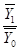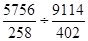= 0,984;
I пост сост =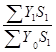 
= 
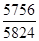= 0,988;
Iструктуры=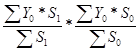 
= 
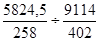=0,996;
IS =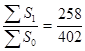 
= 0,64;
Абсолютное изменение валового надоя:
а) за счет изменения продуктивности Δу = ∑ S1*Y1 – ∑ Y0*S1 = – 68,5 ц
б) за счет изменения структуры Δ стр =(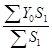
– 
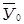) × ∑ S1 = -24,78 ц
в) за счет изменения поголовья Δs =(∑ S1 - ∑ S0) × 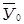= – 3264,7 ц
Общее изменение валового надоя:
ΔВС == ∑ S1Y1 – ∑ S0 Y0= – 3358 ц или Δу + Δ стр + ΔS = – 3358 ц
Индекс переменного состава характеризует совместное влияние факторов на результат. То есть значение индекса равное 0, 984 говорит о том, что общая продуктивность по 2-м хозяйствам сократилась на 1,6% в отчётном периоде по сравнению с базисным и это было обусловлено влиянием обоих факторов, как поголовья, так и среднего надоя.
Валовой надой по двум предприятиям уменьшился на 63% или на3358 ц. это произошло по нескольким причинам: из-за изменения поголовья, то есть за счет его уменьшения на 36 % — уменьшился на 3264,7 ц; из-за уменьшения продуктивности на 1,2%, — уменьшился на 68,5 ц; из-за изменения структуры поголовья (то есть увеличение менее продуктивного скота и уменьшение более продуктивного) — уменьшился на 24,78 ц.