Лекция 1.
Технологии управления данными в системах поддержки принятия решений
Определение СППР. Концептуальная модель СППР (мб блок-схема). Интерфейс, блок анализа, базы данных, базы знаний и т.д. Кто пользователи СППР? Какие задачи решаются? Какое ПО используется? Области применения?
Подсистемы интеллектуального анализа (Data Mining)
Data Mining – исследование и обнаружение “машиной” (алгоритмами, средствами ИИ) в данных, скрытых знаний, которые ранее не были известны, нетривиальны, практически полезны, доступны для интерпретации человеком.
Операции на множестве – при умножении элемента на другое, результатом является элемент того же множества.
Расстояние между объектами (мера различий)
Расстоянием d называется двухместная действительная функция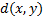 
, обладающая следующими свойствами (для всех входящих переменных):
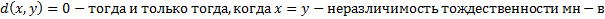
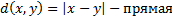
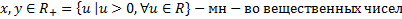
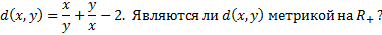
Необходимые сведения из теории матриц
След квадратной матрицы – сумма диагональных элементов
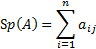
Норма матрицы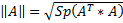 
, где матрица A любая, т.е. размерность n x m
Расстояние между матрицами
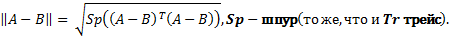
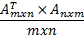
Скалярное произведение матриц и след
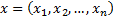
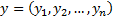
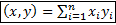– невырожденная симметричная билинейная форма
Скалярное произведение
_____________________________________________________________________________________
Пусть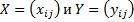 
– матрицы одного размера
Тогда их скалярным произведением назовем величину
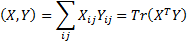
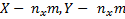
Квадрат длины матрицы X есть
Свойства следа матрицы
1. 
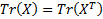
2. 
3. 
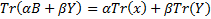
Матрица объект-признак
Столбцы признакам, строки соответствуют объектам
(…)
//Миркин Б.Г. Качественный анализ данных
Операции многомерного дифференцирования.
Комплексные числа
Метод анализа иерархий
Экспертные многокритериальные системы (!)
Если альтернатива A > B, а B > C => (A > C) ~ 10%
Проблема согласования
Слабоструктурированные системы
Когнитивное модулирование
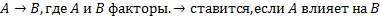
Если увеличение A ведет к увеличению B и уменьшение A ведет к уменьшению B, то
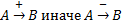
Согласованность знакового графа (!)
Цикл должен быть положительным, тогда результат будет успешным. (сбалансирован)
Метод главных компонентов
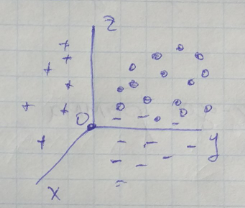
Многомерные данные > 3
Проекционный метод
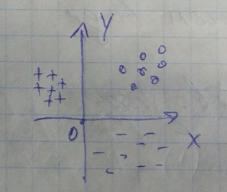
//Операторы проектирования (Миркин)
Матрица объект-признак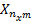 
1. Стандартизация матрицы объект-признак
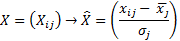
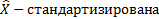
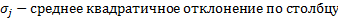
Начало координат переводим в центр средних значений. Еще проводим и нормировку.
2. 
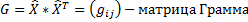, где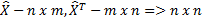 
Легко видеть, что каждый элемент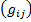 
получен в виде скалярного произведения i-той строки на j-ый столбец
Умножаем в матричном виде.
Собственный вектор и собственные значения.
Дана квадратичная матрица A
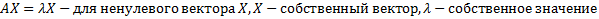
Вектор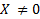 
Результат проектирования на lую ось
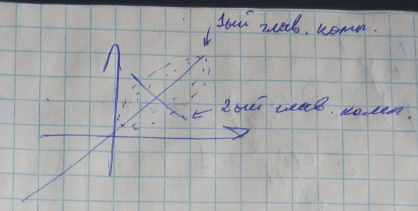
Первый главный компонент – собственный вектор матрицы G отвечающий собственному максимальному значению
Второй главный компонент – собственный вектор матрицы G отвечающий следующему по величине собственному значению и т.д.
Спектр – совокупность максимальных значений
Ортогональный базис
Ряд Фурье
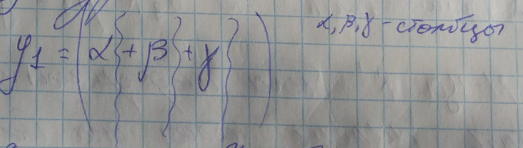
Дисперсия. Чем больше дисперсия, тем больше разнообразия.
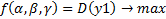
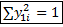– нормировка
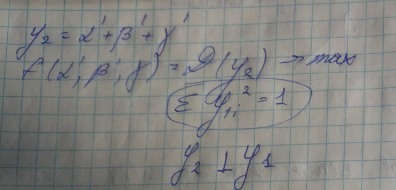
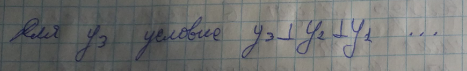
//Задача. Цветная фотография. Спектры R,G,B. С помощью метода главных компонент улучшить фотографию
чтобы матрица R’ была информативна.
Посчитать дисперсию, чтобы она была максимальная (для R’,B’,G’)
Вектора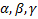 
– должны быть ортогональны. Визуализировать.
Лекция 2.
Визуализация многомерных данных
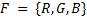
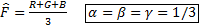
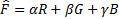
Дисперсия – D
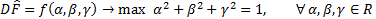
X – объект-признак
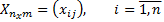
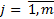
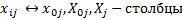
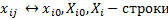
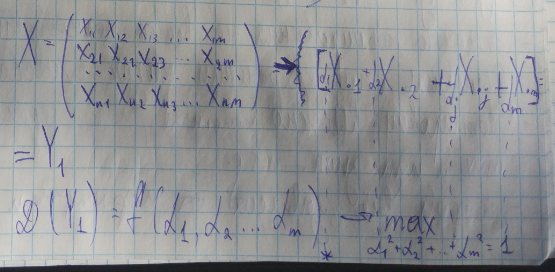
1. Операции с матрицей объект-признак
Централизация
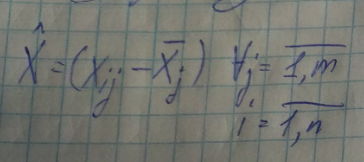
Цель нормировки – уйти от размерных величин
2. Операция нормирования
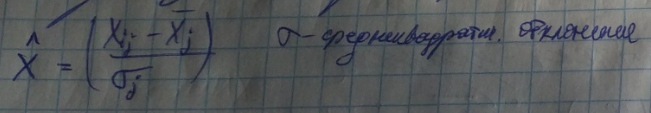
Евклидова матрица.
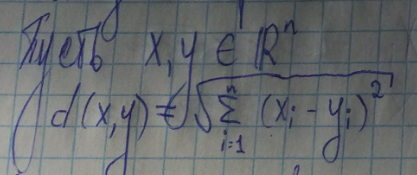
· Операцию нормирования не всегда целесообразно выполнять (при сохранении физического смысла)
· Нормировку можно выполнять и к среднему, max и min значению и т.д.
· Порой все зависит от нормировки
Наилучшая нормировка по среднеквадратичному отклонению.
Центрирование + нормирование = операция стандартизации
Задача
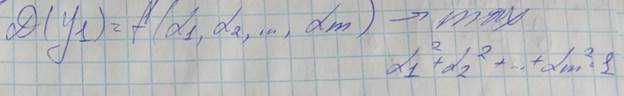
Решение
1. Провести операцию стандартизации. Будем обозначать стандартизированную матрицу объект-признак как X
2. 
3. Находим собственный вектор матрицы грамма, имеющий максимальное собственное значение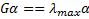 
Теорема Перона
Y1 является собственным вектором матрицы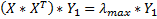 
~~
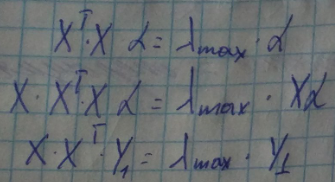
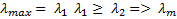
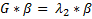
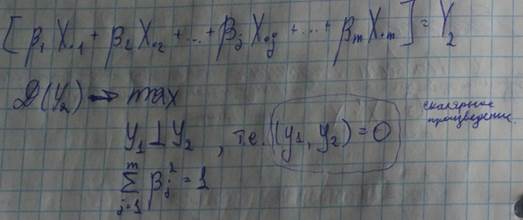
Решение
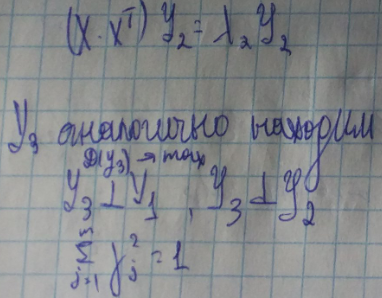
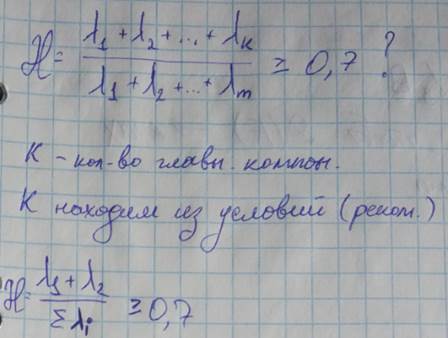
//Цветы Ириса
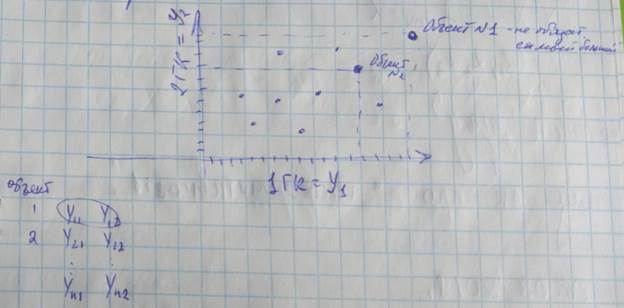
//К слу. Среде визуализировать в Матлаб на примере цветов ириса
//Ч/б фото из цветной
