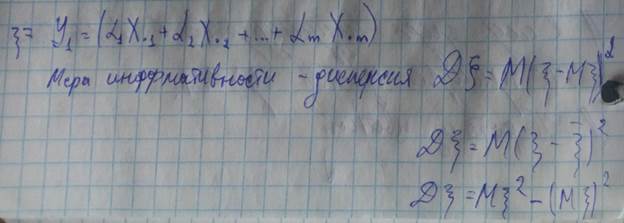
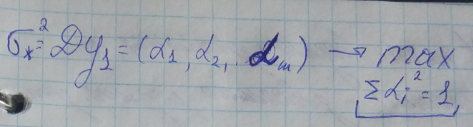
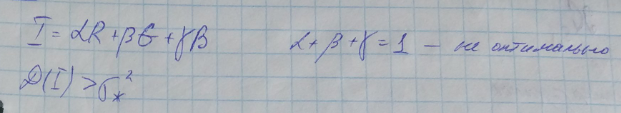
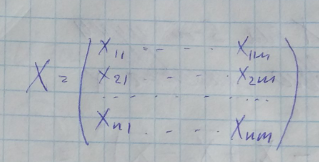
- Избавление от неинформативных признаков.
Неинформативным признаком в задаче классификации называется признак, который принимает близкие значения на объектах одного класса и существенно на объектах, принадлежащих различным классам.
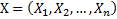
Имеется K – групп, внутри каждой группы признак X имеет близкие значения, а между группами – значимо различные значения
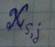 S – номер группы, j – jый номер в S-той группе
S – номер группы, j – jый номер в S-той группе
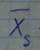 - среднее значение признака X для S-ой группы
- среднее значение признака X для S-ой группы
 - среднее значение для всего массива X
- среднее значение для всего массива X
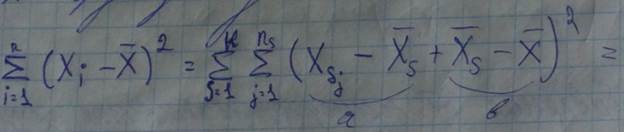
K – групп
 – количество элементов в S-ой группе
– количество элементов в S-ой группе
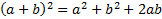

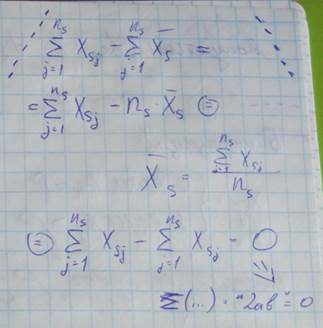
И так,
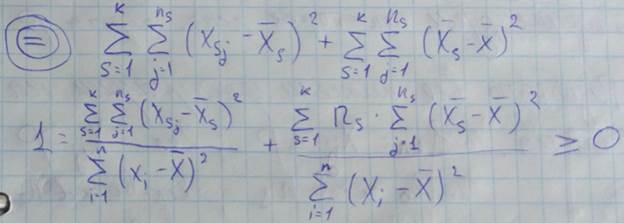
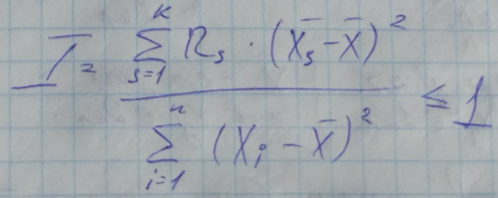
I – оценка информативности признака в задачах классификации
Допустим 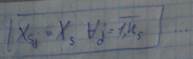
Бинаризация
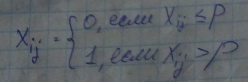
Определяем порог p из информативности 
1) Зафиксируем некоторое значение порога p
2) Разобьем все пиксели фотографии на 2 класса.
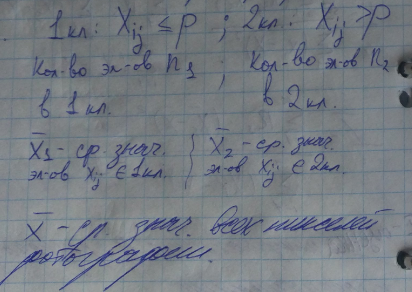
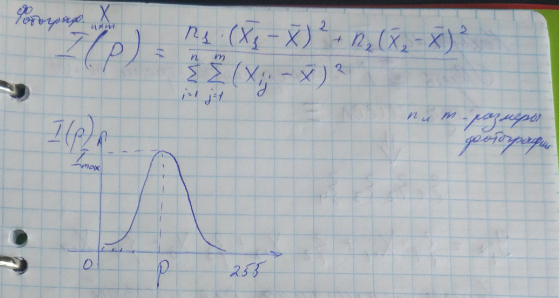
……..
Цветы Ириса
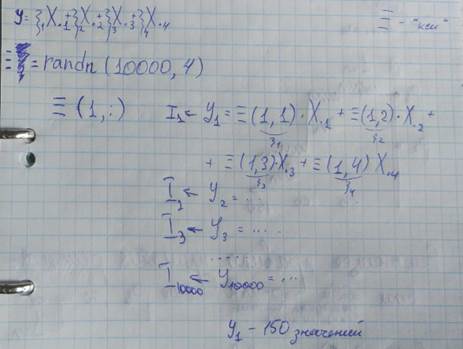
Находим I max
Пусть I* - номер соответствующей строки матрицы случайных числе

Нашли реализацию, для которой информативность максимальная, т.е равна I max
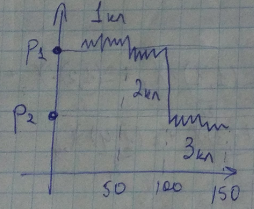
Решающее правило принятия решения:
Если обобщенная характеристика (найденная линейная комбинация) * больше p1, то характеристика 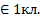
Если 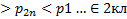
Если 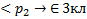
Лекция 4.
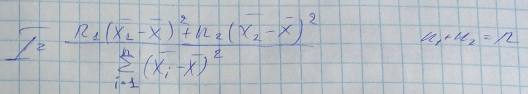
Задача нейронной сети (для классификации) – решить задачу классификации (по признакам информативности)
Формируем матрицу D
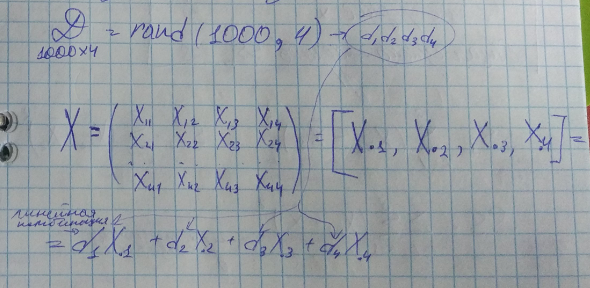
Будет задача распознавания кардиограмм (задача классификации)
//Решить задачу для цветов Ириса (вышеописанную)
Дисперсионный анализ
| X1 | X2 | |
| Наблюдение 1 Наблюдение 2 Наблюдение 3 | ||
Среднее 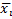 Сумма квадратов
Сумма квадратов 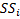
| ||
Общее среднее 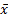 Общая сумма квадратов SS
Общая сумма квадратов SS
|
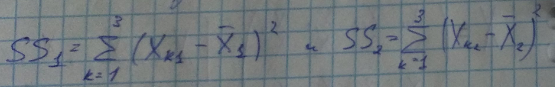
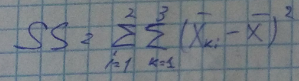 - Межгрупповая дисперсия
- Межгрупповая дисперсия
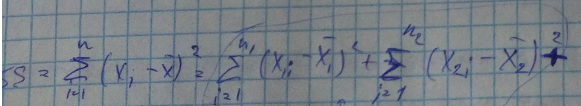
- Внутригрупповая дисперсия SS фактическая
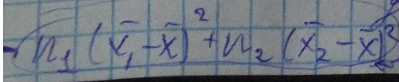 - Межгрупповая дисперсия SS. Считать не обязательным. Достаточная
- Межгрупповая дисперсия SS. Считать не обязательным. Достаточная
SS факт. – фактическая
SS ост. – достаточная

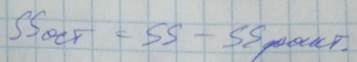
//Книга глава 11. Фролова
Проверка статистической значимости различия средних (используется пример из табл. 3)
m = 3 (количество наблюдений)
p = 2 (количество групп)

Критерий Фишера-Снедекора
 - распределены по Фишеру
- распределены по Фишеру
m – количество элементов в каждой группе одинаковое.
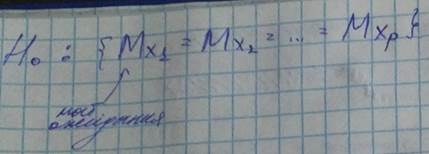

В Матлаб:
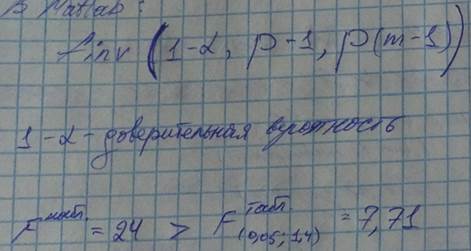
//Дома посчитать  (откуда берется) из табл. 11.1 книжки
(откуда берется) из табл. 11.1 книжки
//В Матлаб искл. Finv – (11.2 из книжки)
//Распространить эту технологию для разработки правила, в соответствии с которым определяются неинформативные признаки (формальный метод), которые необходимо исключить (на цветах ириса). Область – однофакторный дисперсионный анализ.
Шкалы
Имеется 5 шкал (обычно используются 5, но их бесконечно много)
Качественные:
1) Номинальная. Качественная школа, предполагающая любые взаимно-однозначные операции
2) Ранговая (порядковая). Позволяет проранжировать все величины.
Количественные:
3) Шкала интервалов (интервальная)
4) Шкала отношений
5) Абсолютная шкала
Измерения в СППР называют процедуру, с помощью которой, изучаемым объектом и отношением между ними ставятся в соответствие элементы и отношения, принадлежащие некоторой математической структуре, т.е. это множество элементов той или иной математической природы и совокупность отношений между их элементами.
Самый простой случай, когда элементы являются действительными числами и измерения сводятся к приписыванию объекту того или иного числа (рост, вес, скорость реакции и т.д.)
При измерении каждому объекту приписывают определенный элемент, используемой математической структуры.
Шкала – инструмент, способ измерения (способ кодировки, способ приписывания объекту числа).
| Допустимые преобразования | Тип шкалы | Примеры |
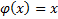
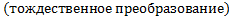
| Абсолютная | Пересчет предметов |
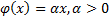 (преобразованное подобие)
(преобразованное подобие)
| Шкала отношений | Масса тела Температура (шкала Кельвина) |
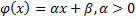 (положительное линейное преобразование)
(положительное линейное преобразование)
| Интервальная | Температура (шкала Фаренгейта и Цельсия) |
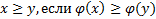 (монотонно возрастающее преобразование)
(монотонно возрастающее преобразование)
| Порядковая | Предпочтения Твердость Качество воздуха Баллы интеллектуального теста |
| Любое взаимно-однозначное преобразование | Номинальная | Номера игроков Номера разных планов |
Интервальная шкала
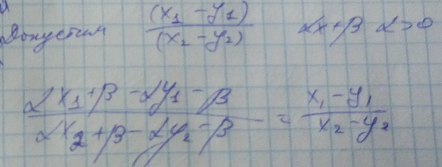
//Книжка Data Mining Чубукова

Лекция 5.
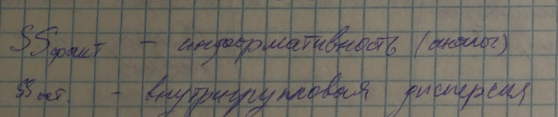
Возьмем признак X1
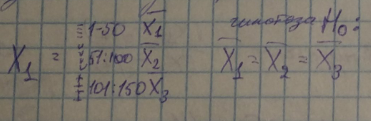
Необходимо посчитать общую дисперсию SS
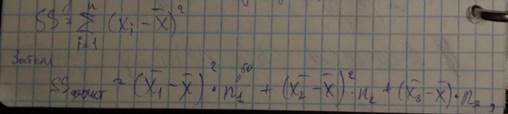

Строим отношения Фишера
F = …, H1: конкурирующая гипотеза (альтернативная), что есть отрицание H0

Если F – верна конкурирующая гипотеза
F табличная:
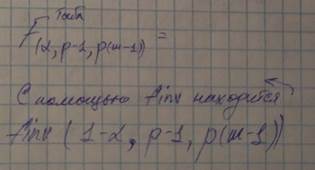
*Если 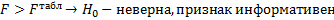
Для данного случая
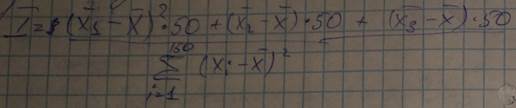
Когда 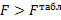 для признака
для признака 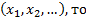 прекращаем *
прекращаем *
//О.И. Ларичев Теория и методы принятия решений (от 2006г)