Множество Паретто – множество альтернатив
Нахождение Паретто оптимальное решение.
Крайние точки конечного множества
Пусть задано конечное множество на плоскости
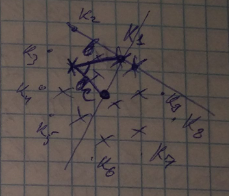
Точка X0 называется крайней точкой для конечного множества X, если
1) 
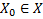
2) С другой стороны, существует такая прямая, проходящая через эту точку, что все точки этого множества лежат по одну сторону от этой прямой.
Алгоритм поиска крайних точек (Поиск Паретто оптимальных решений):
1) Найти центр тяжести (центроид). Обозначим точку C.
2) Найти наиболее удаленную точку от центроида. Эта точка является 1й крайней точкой. Присваиваем ей номер 1 (k1)
3) Через k1 и C проводим прямую
4) Зафиксируем порядок обхода (например, против часовой стрелки). Берем любую точку. Соединяем ее с C и k1.
Посчитаем векторное произведение
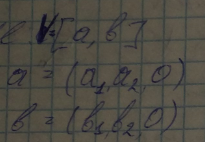
Если V имеет проекцию на ось Z, то положительно
Точка лежит левее прямой (k1 C)
Выбираем все положительные проекции точки. Для них ищем новый центроид. Все тоже самое с k1 и новым центроидом.
Делаем до того момента, пока не дотигнем следующей крайней точки.
Далее все тоже самое, но с K2 и т.д. В конце приходим к k1.
Когда соединим крайние точки, то точки внутри этого многоугольника являются точками этого класса (обучающая выборка)
//Сделать алгоритм по крайним точкам. Необходима нумерация крайних точек.
Главное – взять альтернативу (принять решение) <- взять Паретто оптимальное решение.
Найдя крайние точки они гарантировано Паретто оптимальные.
//Математические методы. Иванов … Глава 4.
Методы обработки групповых мнений и принятия коллективных решений.
Необходимо знать 3 метода: ранжирование, нормирование, парное сравнение.
//Уделить большое внимание нормулировке.
Метод наименьших квадратов.
1. Есть ли групповое мнение?
2. Если есть, то какое?
3. Коэффициент конкордации W (Гл. 4.4)
Лекция 6. МАИ
Метод анализа иерархий
- Градиент ф-ции
Геометрический градиент доказывает на направление наискорейшего сравнительный смысл
//стр 115-129 – Ларичев. МАИ
Критерий – показатель качества.
//Томас Саати – автор метода. Метод анализа иерархий. 1978г. – метод качелей
//Лобачевский (геометрия). Жизнь замечательных людей
Max 9 альтернатив (лучше 5-7)
Шкала относительной важности:
Равная важность -------------------1
Умеренное превосходство -----3
Существенное превосходство—5
Значительное превосходство---7
Очень большое превосходство-9
Четные – промежуточные значения
Допустим A1A2 - 3, то A2 A1 - 1/3
Формируется матрица кривых сравнений. Сначала для критериев. Затем по критериям для альтернатив. Главный вектор приоритетов.
Матрица парных сравнений в МАИ должна быть обратно симметричная!!!
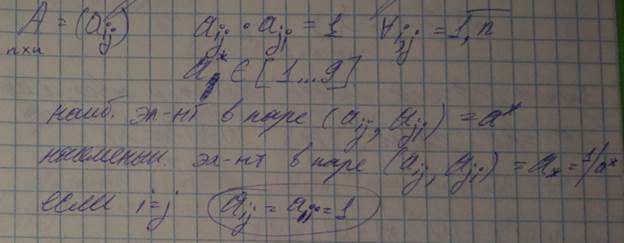
*Вопрос. Какая по вашему мнению обратно-симметричная матрица является наилучшей? (в *наилучшей степени отражает различия между сравниваемыми элементами)
Вектор приоритетов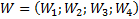 
всегда столбец
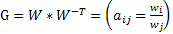Сверхтранзитивная матрица
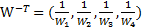
Если альтернативы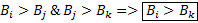 
X