РЯДЫ
Цель работы: ознакомиться с возможностями MatLab при решении задач по разложению функций в ряд и определению суммы членов ряда.
Теоретические сведения
Числовые ряды
Числовой ряд – это последовательность чисел:
Элементы последовательности 
– члены ряда.
n -ая частичная сумма ряда – сумма первых членов ряда:
.
Если последовательность конечных сумм ряда имеет конечный предел, то ряд сходится.
Если предел последовательности частичных сумм не существует или бесконечен, то ряд расходится.
Для вычисления суммы ряда в MatLab используется функция: symsum(fun[,var,a,b]).
где fun – символьное выражение, обозначающее общий член суммы ряда, зависящий от переменной var, изменяющейся от a до b.
Пример.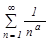 
– обобщенный гармонический ряд, сходящийся при 
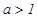и расходящийся при 
.
>>f=sym('1/n^2');
>>symsum(f,'n',1,inf)
ans=
1/6*pi^2 – ряд сходится.
>>f=sym('1/n');
>>symsum(f,'n',1,inf)
ans=
Inf – ряд расходится.
Иногда для исследования сходимости одного положительного ряда его сравнивают с другим 
, о котором уже известно сходится он или расходится.
Если 
, то из сходимости следует сходимость и наоборот: из расходимости следует расходимость . Для сравнения гармонического ряда с заданным строят график, по которому определяют он больше или меньше заданного.
Пример. Исследовать на сходимость ряд 
Сравним заданный ряд с гармоническим 
.
На графике показано, что гармонический ряд больше.
Гармонический ряд расходится, следовательно, расходится и заданный ряд.
>> f=sym('cos(n)/n');
>> symsum(f,'n',1,inf)
ans =
sum(cos(n)/n,n = 1.. inf)
>> f=sym('1/n');
>> symsum(f,'n',1,inf)
ans =
inf
Сходимость по Даламберу
Если в положительном ряде отношение 
(последующего члена к предыдущему) при 
имеет предел 
, то возможны три случая):
Пример. Исследовать ряд на сходимость: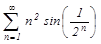 
.
>> f=sym('n^2*sin(1/(2^n))');
>> symsum(f,'n',1,inf)
ans =
sum(n^2*sin(1/(2^n)),n = 1.. inf)
>> U1=sym('n^2*sin(1/(2^n))');
>> U2=sym('(n+1)^2*sin(1/2^(n+1))');
>> limit(U2/U1,'n',inf)
ans =
1/2
После соответствующих вычислений q =1/2<1, из чего вытекает, что ряд сходится.
Функция limit(fun,x,inf) возвращает предел символьного выражения fun в точке x, стремящейся к бесконечности.
Интегральный признак Коши
Если каждый член положительного ряда меньше предшествующего, то рассматривают несобственный интеграл:
,
где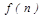 
– непрерывная убывающая функция, принимающая при 
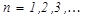значения 
.
Ряд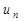 
сходится или расходится, в зависимости от того, сходится или расходится несобственный интеграл.
Пример. Исследовать ряд на сходимость: 
.
>> f=sym('1/n*ln((n+1)/n)');
>> symsum(f,'n',1,inf)
ans =
sum(1/n*log((n+1)/n),n = 1.. inf) – неопределенность
>> I=int(f,'n',1,inf)
I =
1/12*pi^2
>> vpa(I,4)
ans =
0,8226
Несобственный интеграл сходится, так как имеет конечный предел, значит, сходится и ряд.
Функция int(f,'n',1,inf) используется для символьного вычисления неопределенных интегралов, где f – подынтегральное выражение, n – переменная интегрирования.
Функция vpa(I,4) – численное решение (оценка с точностью до 4-х знаков).
Функциональные и степенные ряды
Функциональный ряд – ряд, члены которого являются функциями независимой переменной х.
Степенной ряд – функциональный ряд 
Радиус сходимости степенного ряда называют такое число R, при котором для всех x, 
степенной ряд сходится, а для всех x,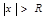 
– расходится.
Интервал сходимости – интервал от - R до R.
Пример. Вычислить интервал сходимости ряда 
.
По определению, при сходимости степенного ряда . Исследуем ряд, состоящий из абсолютных членов исходного, при помощи признака Даламбера. Если удастся найти предел отношения последующего члена к предыдущему, то в отличие от числового ряда, он будет содержать множитель 
или некоторую его степень. Для тех значений, при которых предел будет меньше единицы, ряд сходится, а для тех, при которых больше – расходится. Если найденный предел для любого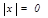 
, то ряд сходится при всех х. Если при всех 
предел окажется равным бесконечности, то ряд будет всюду расходиться.
>> syms n x
>> U1=sym('2^n*x^n/3^n/n');
>> U2=sym('2^(n+1)*x^(n+1)/3^(n+1)/(n+1)');
>> s=simplify(U2/U1)
% функция simplify применяется для того, чтобы упростить выражение (U2/U1)
s =
2/3*x/(n+1)*n
% нахождение предела s
>> limit(s,'n',inf)
ans =
2/3*x
>> limit(-s,'n',inf)
ans =
-2/3*x
>> t=solve(abs (2/3* x-1),x)
t =
3/2
% при t = 3/2 ряд расходится
>> symsum(subs(U1,x,t),'n',1,inf)
ans =
inf
% при t = -3/2 ряд сходится
>> symsum(subs(U1,x,-t),'n',1,inf)
ans =
-log(2)