Одномерная цепочка с двумя атомами в примитивной ячейке

Исследуем теперь колебания цепочки, элементарная ячейка которой состоит из двух атомов с разными массами: M ₁ и M ₂, для определенности положим M ₁< M ₂. Период цепочки (расстояние между узлами ее решетки Браве) как и прежде обозначим через a (рис. 3). Для простоты будем считать, что ''пружинки'' соединяющие атомы имеют одинаковую жесткость γ.

Рис. 1. 3. Одномерная цепочка с двумя атомами в примитивной ячейке и ее решетка Браве.

Запишем закон Ньютона для двух атомов n -й ячейки:

(22).

Здесь u_n и v_n – смещения соответственно маленького и большого атома n -й ячейки из положения равновесия.

Будем, как и в случае цепочки с одним атомом в примитивной ячейке, искать решение в виде плоской гармонической волны:

(23).

Амплитуды колебаний маленького и большого атомов A и B в общем случае разные как по абсолютной величине, так и по фазе.

После подстановки (23) в (22) получим линейную однородную систему уравнений для A и B:

– M ₁ ω ² A= γ (Be^ika + B –2 A)

– M ₂ ω ² B= γ (A + Ae ^{– ika} –2 B) (24).

Перепишем ее в стандартном виде:

(25)

Такая система имеет решения лишь в том случае, когда ее определитель равен нулю. Приравнивая нулю определитель (25) получим уравнение, связывающее ω и k, т. е. дисперсионное уравнение:

M ₁ M ₂ ω ⁴ – 2 γ (M ₁+ M ₂) ω ²+2 γ ²(1–cos ka) = 0 (26).

Это уравнение удобно переписать, использую приведенную массу атомов примитивной ячейки μ:

(27).

(28)

Его решения имеют вид:

(29)

или (30).

Величина 4 μ ²/(M ₁ M ₂) при любых M ₁, M ₂ не превосходит единицы, поэтому подкоренное выражение всегда неотрицательно.

Трехмерный кристалл

Мы рассмотрели колебания в одномерной цепочке. Подобным образом могут быть описаны и колебания решетки трехмерного кристалла.

Предположим, что примитивная ячейка кристалла состоит из l атомов. Каждый атом ячейки будем обозначать индексом s, этот индекс принимает l различных значений. Любой атом кристалла однозначно определяется радиус-вектором , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).

Смещение атомов при колебаниях решетки является линейной комбинацией плоских гармонических волн (точнее, их вещественных частей): (40).

Частота колебаний одинакова для всех атомов кристалла. Амплитуда колебаний зависит от типа атома (индекса s), то есть одинакова для всех однотипных атомов. Направление вектора амплитуды может, вообще говоря, быть каким угодно.

Индекс j обозначает ветвь колебаний. Волновой вектор и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости и являются непрерывными функциями.

Если примитивная ячейка кристалла содержит l атомов, то число ветвей равно 3 l. Таким образом, каждому значению волнового вектора соответствуют 3 l разных колебаний.

Три из этих ветвей – акустические, в предельном случае длинных волн их частота пропорциональна длине волнового вектора ω = 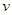| k |. Однако скорость звука 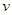зависит от направления распространения волны, то есть от направления вектора . В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.

Остальные 3 l –3 ветвей – оптические, при их частота отлична от нуля.

По направлению амплитуды относительно волнового вектора акустические колебания можно разделить на продольное и два поперечных. Как правило, скорость звука у продольного колебания больше, чем у поперечных.

У кристаллов со структурой алмаза или цинковой обманки примитивная ячейка содержит 2 атома. Соответственно, кроме трех акустических, эти кристаллы обладают тремя оптическими ветвями колебаний, из которых также можно выделить продольную и две поперечных ветви.

Как и в одномерном случае, волновые вектора, отличающиеся друг от друга на вектор обратной решетки, соответствуют одному и тому же колебанию. По этой причине достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна.

Количество разрешенных волновых векторов в зоне Бриллюэна равно N = V / v ₀ – числу примитивных ячеек в нормировочном объеме кристалла V = L ³ (v ₀ – объем примитивной ячейки). Действительно, плотность разрешенных волновых векторов в обратном пространстве равна V /(2 π)³, т. е. в объеме обратного пространства Δ ³ k содержится Δ ³ k · V /(2 π)³ разрешенных волновых векторов. Объем зоны Бриллюэна – объем примитивной ячейки обратной решетки — равен (2 π)³/ v ₀, и для числа разрешенных состояний получаем (2 π)³/ v ₀· V /(2 π)³ = V / v ₀ = N.

Число ветвей — 3 l, поэтому полное число колебаний равно 3 lN — утроенному числу атомов кристалла в объеме L ³, т. е. числу степеней свободы механической системы.