Энергию колебаний и теплоемкость решетки будем рассчитывать для единичного объема кристалла, т. е. положим нормировочный объем равным единице: V = L 3 = 1.
Чтобы вычислить среднюю энергию колебаний кристаллической решетки, нужно просуммировать среднюю энергию всех типов колебаний (всех состояний фононов):
(43).
Проще всего это сделать при высоких температурах, когда для частот всех колебаний выполняется неравенство ħ ωjk << kT (классический предел). Тогда средняя энергия, приходящаяся на каждое колебание, равна kBT, всего колебаний 3 lN = 3 lN, для полной энергии E получаем:
(44).
Так как N – число примитивных ячеек кристалла в единице объема, то N = 1/ v 0, где v 0 – объем примитивной ячейки.
Теплоемкость решетки при высоких температурах постоянна (закон Дюлонга и Пти): CV = 3 lNk (45).
При невысоких температурах все сложнее. Чтобы точно вычислить энергию решетки, то есть сосчитать сумму (45), необходимо знать дисперсионные зависимости для всех ветвей колебаний. И даже при условии, что зависимости эти известны, аналитическое выражение для энергии получить практически невозможно.
Поэтому для нахождения энергии и теплоемкости решетки применяют различные приближения.
Модель Эйнштейна
В модели Эйнштейна предполагается, что частоты всех фононов одинаковы: ωjk = ω 1 (46).
Тогда для энергии получаем:
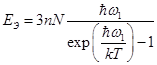(47).
При высоких температурах, kBT >>ħ ω 1, эта зависимость приводит к выражению (45) для энергии и закону Дюлонга и Пти (46) для теплоемкости.
При низких температурах, kT <<ħ ω 1, энергия колебаний и теплоемкость экспоненциально уменьшаются:
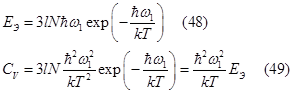
Модель Эйнштейна хорошо описывает вклад в энергию и теплоемкость оптических ветвей фононов, у которых частота слабо зависит от волнового вектора и ее можно считать постоянной. Чтобы учесть только оптические ветви, частоту которых мы полагаем равной ω 1, нужно вместо 3 l писать число этих ветвей. В общем случае, частоты разных оптических ветвей могут сильно отличаться друг от друга и их вклад в энергию и теплоемкость нужно учитывать отдельно.
|
|
Модель Дебая
Опыт показывает, что теплоемкость действительно падает с уменьшением температуры, но не экспоненциально, а пропорционально T 3. Дело в том, что при любых, сколь угодно низких температурах в кристалле найдутся колебания, энергия фонона которых меньше kBT. Это – длинноволновые акустические колебания. Именно такие колебания, точнее те из них, частота которых меньше kBT /ħ, вносят основной вклад в энергию при низких температурах. Колебания с большими частотами (оптические и более коротковолновые акустические) ''заморожены'': фононов этих колебаний экспоненциально мало.
Сделаем простую оценку. Вклад в энергию вносят фононы, энергия которых меньше kT. Пусть скорость звука j -й акустической ветви равна 
j и не зависит от направления волнового вектора: ω = 
j | k |. Тогда вклад в энергию дают колебания с волновыми векторами, меньшими kmax = kBT /(ħ j). Плотность разрешенных значений волновых векторов в k -пространстве кристалла равна V /(2 π)3, поэтому внутри сферы радиуса kmax содержится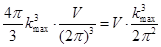 
разрешенных значений волновых векторов. Это число колебаний одной акустической ветви, вносящих существенный вклад в энергию. На каждое такое колебание приходится энергия порядка kT. Для энергии колебаний одной акустической ветви получаем:
|
|
(50).
Так как мы вычисляем энергию и теплоемкость единицы объема кристалла, то в (50) мы положили V = 1.
Таким образом, вклад одной акустической ветви в теплоемкость пропорционален T 3:
(51).
Чтобы получить полную энергию и теплоемкость, надо сложить вклады от трех акустических ветвей:
(52),
где через 
j обозначена скорости звука j -й акустической ветви.
Мы сделали достаточно грубую оценку, поэтому к численным коэффициентам в последних двух выражениях не стоит относиться серьезно. Тем не менее, эта оценка дает правильную зависимость энергии и теплоемкости от температуры и скорости звука.
Посчитаем теперь энергию решетки при низких температурах более аккуратно.
Формула (44) имеет вид суммы по различным колебаниям (различным состояниям фононов) определенной величины, которая зависит только от энергии фонона:
Такие суммы встречаются довольно часто. Так как f зависит только от энергии фонона, то от суммы по состояниям можно перейти к интегралу по энергии:
(54).
Здесь 
- плотность состояний фононов. Напомним, что 
- это число состояний квазичастиц (фононов) в единице объема с энергиями от 
до 
, то есть число различных колебаний с такими энергиями.
Суммарная плотность состояний складывается из плотности состояний разных ветвей: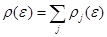 
; плотность состояний ветви определяется ее законом дисперсии 
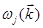. Аналитически получить законы дисперсии и плотности состояний фононов реальных кристаллов практически невозможно.
|
|
Однако при низких температурах энергия и теплоемкость определяются длинноволновыми акустическими фононами. Плотность состояний акустических фононов нам известна, мы получили ее в качестве примера, когда вводили само понятие плотности состояний 
. Если для j -й акустической ветви ω =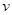 
j | k |, то:
(55).
Плотность состояний длинноволновых колебаний всех акустических ветвей получается суммированием по трем акустическим ветвям:
(56), где - ''усредненная'' скорость звука:
(57).
Линейный закон дисперсии ω = | k | и соответствующая плотность состояний верны только для малых k. При больших значениях волнового вектора закон дисперсии и плотность состояний имеют более сложный вид.
Однако при низких температурах вклад в энергию и теплоемкость вносят как раз только длинноволновые фононы, а при высоких температурах вид плотности состояний не важен, так как в этом случае на каждое колебание приходится энергия kT. Чтобы получить выражение, которое давало бы правильные предельные зависимости при низких и высоких температурах, Дебай предложил считать, что закон дисперсии ω = | k | выполняется и при больших k. Максимальное значение волнового вектора kD при этом выбирается так, чтобы в шаре радиуса kD содержалось столько разрешенных значений волновых векторов, сколько их содержится в зоне Бриллюэна, N = 1/ v 0. Иными словами, объем этого шара должен быть равен объему зоны Бриллюэна (2 π)3/ v 0, откуда
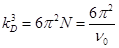(58).
Таким образом, сохраняя число акустических колебаний, мы заменяем первую зону Бриллюэна сферой, а реальный закон дисперсии – линейным. Фонон с волновым вектором kD имеет энергию 
. Соответствующая 
температура:
(59), называется температурой Дебая.
В таком приближении мы можем вычислить вклад акустических ветвей в энергию и теплоемкость решетки:
При низких температурах, T << θ, верхний предел интеграла много больше единицы. Благодаря экспоненте в знаменателе интеграл сходится очень быстро, что позволяет положить верхний предел равным бесконечности. Значение такого интеграла известно: 
(61).
Для энергии акустических колебаний при низких температурах получаем:
(62)
Откуда следует, что теплоемкость решетки при низких температурах пропорциональна T 3:
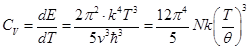(63).
При высоких температурах, T >> θ, верхний предел интегрирования мал, поэтому можно считать, что exp(x)–1≈ x, таким образом:
(64).
Тогда: E = 3 NkT и CV = 3 Nk.
Это закон Дюлонга и Пти, только вместо полного числа колебаний 3 lN стоит число колебаний акустических ветвей 3 N. (При высоких температурах на каждое колебание приходится средняя энергия kT, полное число акустических колебаний равно 3 N, поэтому вклад акустических ветвей в энергию равен 3 NkT).
В пределе низких и высоких температур модель Дебая дает точные значения для вклада акустических ветвей в энергию и теплоемкость. В области же промежуточных температур, T ~ θ, эта модель лишь аппроксимирует реальную зависимость энергии и теплоемкости от температуры.
Температура Дебая разделяет две температурные области. В области низких температур на энергию и теплоемкость решетки сильное влияние оказывают квантовые эффекты (''вымерзание'' высокочастотных колебаний). В области высоких температур эти эффекты не существенны, и теплоемкость может быть вычислена в классическом приближении. Для большинства кристаллов температура Дебая лежит в интервале от 100 до 300 K.
Чтобы получить полную энергию и теплоемкость кристаллической решетки, надо к вкладу акустических колебаний прибавить вклад оптических ветвей, для которого хорошим приближением является модель Эйнштейна. Этот вклад пренебрежимо мал при низких температурах. При высоких температурах вклады всех ветвей в энергию и теплоемкость равны.
Выводы
В данной работе были рассмотрены явления колебаний кристаллической решетки твердого тела и поставлено в соответствие рассмотренным колебаниям квазичастицы – фононы. Для одномерных цепочек атомов проведен математический анализ колебаний и рассмотрен оптическую и акустическую составляющую колебаний. Оптические и акустические фононы отвечают за различные свойства кристаллов. Оптические колебания (фононы) играют основную роль в процессах поглощения взаимодействия света с кристаллом. В частности поглощение инфракрасного излучения ионными кристаллами обусловлено именно оптическими колебаниями решетки.
Акустические колебания играют основную роль в определении тепловых свойств кристаллов – теплоемкости, теплопроводности, теплового расширения.
В качестве примера рассмотрено нахождение теплоемкости тел при различных температурах и вклад оптических и акустических колебаний в величину теплоемкости при различных температурах.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Ансельм А. И. Введение в теорию полупроводников. – М.: Мир, 1965. – 588 с.
2. Басс Ф. Г. Электроны и фононы в ограниченных полупроводниках. – М.: Наука, 1984. – 287 с.
3. Дущенко В. П., Кучерук И. М. Общая физика. – К.: Высшая школа, 1995. – 430 с.
4. Епифанов Г. И. Физические основы микроэлектроники. М.:
Советское радио, 1971, 374 с.
5. Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.
6. Кухлинг Х. Справочник по физике: Пер. с нем. – М.: Мир, 1983. – 520 с.
7. Случинская И. А. Основы материаловедения и технологи
полупроводников. М.: Либрус, 2002, 376 с.
8. Харрисон У. Теория твёрдого тела. – М.:Мир. – 1978. – 616 с.
9. Шалимова К. В. Физика полупроводников. М.: Энергия, 1976, 417 с.
10. Яворский Б. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1982. – 846 с.