В соответствии с формулой (1) здесь также должно выполняться соотношение

(7) .

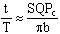Другими словами, время t, необходимое, чтобы планета прошла по эллиптической дуге QP_c, относится ко времени T, затрачиваемому на прохождение всей орбиты, так, как площадь SQP_c относится к общей площади эллипса, где b - радиус малой оси, а большая ось принята за 1. Здесь Кеплер делает предположение, аналогичное тому, какое уже было сделано ранее (см. рис. 4 и 5):

(8) .

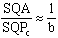Согласно (1)

.

Если подставить это значение в (8) и (7), то в результате простых вычислений получим:

.

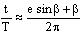Решающий шаг в этом выводе - принятие за исходный пункт уравнения (7) - есть не что иное, как новое и не менее проблематичное применение теоремы Архимеда; теперь она применяется к сектору эллипса, вершиной которого является один из его фокусов, в котором помещается Солнце.

Теперь можно сформулировать два первых закона Кеплера [ср. уравнение (6)]:

(9)

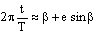
(10)

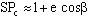
Уравнение (10) говорит о том, что планета движется по эллипсу, в одном из фокусов которого находится Солнце. Уравнение (9) говорит, что в равные промежутки времени радиус "Солнце-планета" пробегает равные площади.

По отношению к Марсу, который является центральной проблемой и исходным пунктом всех рассуждений, это означает, что b и e в уравнении (9) могут быть определены только благодаря ранее отброшенным (даже в усовершенствованном виде) hypothesis vicaria. Поэтому они использовались как при вычислениях SP_с, так и в методе оценки и проверки полученного результата (включая определение трех положений Марса по отношению к одной и той же позиции Земли).

Вот как в действительности обстояли дела с обоснованием двух первых законов Кеплера, обоснованием, которое еще и сегодня часто представляют чем-то таким, что возникло исключительно на базе опыта.

Кстати сказать, теория Птолемея в сравнении с теорией Кеплера вовсе не проигрывает, ибо, во-первых, из-за малости орбитальных эксцентриситетов планет система Птолемея описывает движения планет почти с той же точностью, как теория Кеплера (что же касается Меркурия, то он является для обеих теорий своего рода enfant terrible); во-вторых, аксиома Платона имела ясное философское обоснование, тогда как для Кеплера эллиптическая форма планетарных орбит, естественно, оставалась загадкой. Его попытка обосновать эту форму спецификой движений планет не привела к успеху. В-третьих, то же можно сказать о его усилиях опровергнуть аристотелианскую аргументацию против идеи вращения Земли. Все это было типичными гипотезами ad hoc[50]. Неудивительно, что его "Новая астрономия" была встречена современниками без всякого энтузиазма.

Анализ методов и доказательств, фигурирующих в "Новой астрономии", позволяет нам сказать со всей определенностью: если бы Кеплер следовал доктринам, принятым в теории науки нашего времени, он должен был бы отбросить оба своих закона, значимость которых вряд ли кто-либо сегодня осмелится отрицать. Покажем это на двух примерах: методологии науки Поппера-Лакатоса и индуктивной логики Карнапа.

5.2. "Новая астрономия" Кеплера в свете философии
науки Поппера и Лакатоса

Основной методологический постулат Поппера гласит, что научная теория должна быть фальсифицируемой. Если же фальсификация уже произошла, нам не следует предотвращать крах теории с помощью гипотез ad hoc или других допущений. Поппер пишет: "Если такое решение положительно, то есть если сингулярные следствия оказываются приемлемыми, или верифицированными, то теория может считаться в настоящее время выдержавшей проверку, и у нас нет оснований отказываться от нее. Но если вынесенное решение отрицательное или, иначе говоря, если следствия оказались фальсифицированными, то их фальсификация фальсифицирует и саму теорию, из которой они были логически выведены"[51].

О каком "решении" здесь идет речь? Этот термин означает, что так называемые базисные предложения (под которыми Поппер понимает сингулярные экзистенциальные предложения типа: то-то и то-то существует в такой-то и такой-то пространственно-временной области)[52] противоречат или не противоречат данной теории. Но если теории противоречат только отдельные сингулярные базисные предложения, у нас еще нет основания считать теорию фальсифицированной. "Мы будем считать ее фальсифицированной только в том случае, если нам удалось открыть воспроизводимый эффект, опровергающий теорию. Другими словами, мы признаем фальсификацию только тогда, когда выдвинута и подкреплена эмпирическая гипотеза низкого уровня универсальности, описывающая такой эффект. Подобные гипотезы можно назвать фальсифицирующими гипотезами "^[53]. В качестве примера Поппер приводит высказывание "В нью-йоркском зоопарке живет семейство белых воронов"^[54]; оно фальсифицирует универсальное высказывание "Все вороны черные". Но, добавляет он, "в большинстве случаев до фальсификации некоторой гипотезы мы имеем в запасе другую гипотезу, поэтому фальсифицирующий эксперимент обычно является решающим экспериментом, который помогает нам выбрать одну из двух гипотез"[55].

Итак, фальсифицирующий эффект выводится из другой гипотезы, уже имеющейся в запасе. Конечно, поскольку такого рода решения опираются на базисные предложения, они принципиально могут быть пересмотрены (опять-таки с помощью базисных предложений); но практически мы обычно в какой-то момент прекращаем поиск опровержений и пытаемся закрепиться на избранной позиции. Поэтому Поппер вводит следующее правило: "Мы раз и навсегда отказываемся от того, чтобы приписывать какую-либо подтверждающую силу теории, фальсифицированной в ходе интерсубъективно проверяемого эксперимента"[56].

Однако Кеплер поступал как раз наоборот, когда он использовал результаты ранее фальсифицированных теорий для построения других теорий и затем оценивал последние с помощью первых. Кроме того, он находился в явном противоречии с попперовской методологией еще и в другом отношении. В то время отсутствие каких-либо явлений, указывающих на вращение Земли, рассматривалось как фальсификация всякой формы гелиоцентризма. Чтобы обойти эту фальсификацию, Кеплер пытался делать то, что решительно запрещает Поппер[57], а именно: спасти свою теорию с помощью гипотез ad hoc - и кроме того, с помощью гипотез, не менее проблематичных, чем его астродинамика. Следуй он предписаниям Поппера, ему пришлось бы отказаться от своей теории "раз и навсегда".

Сам Поппер полагает, что успех Кеплера оказался возможным отчасти потому, что "гипотеза окружности, от которой он отталкивался в своем исследовании, была относительно легко фальсифицируемой"[58]. Он прав в той мере, в какой выражение "относительно легко" связано с тем, что гипотеза окружности являлась "трехмерной" ("поскольку для ее фальсификации необходимы по крайней мере четыре принадлежащих данной области сингулярных высказывания, соответствующих четырем точкам ее графического представления"^[59]), тогда как эллиптическая гипотеза являлась "пятимерной" ("поскольку для ее фальсификации необходимы по крайней мере шесть сингулярных высказываний, соответствующих шести точкам на графике"[60]). Однако рассуждения способны скорее лишь завуалировать тот факт, что фальсификация гипотезы о круговой орбите была в высшей степени проблематичной, ибо основана она была на весьма сомнительных посылках.

Пример Кеплера свидетельствует не только о том, что фальсифицирующие базисные предложения трудно распознать (эта трудность, я считаю, не была в достаточной мере осознана Поппером^[61]), но и о том, что отбрасывание теории в каждом случае, когда фальсификация может быть установленной, вовсе не всегда является лучшей стратегией для науки[62].

До сих пор мы сравнивали методологию Кеплера с тем, что сегодня может быть названо классическим попперианством. Однако наши выводы остаются в силе даже с учетом тех улучшений, которые были внесены в эту концепцию И.Лакатосом в последние годы.

По его мнению, существует универсальное правило, по которому можно определить, является ли серия теорий прогрессивной. (Конечно, он совершенно прав, когда говорит о "серии", а не о единичных теориях, ведь фактически каждая теория связана с другими, отличными от нее теориями).

Он пишет:"Будем считать, что такой ряд теорий является теоретически прогрессивным..., если каждая новая теория имеет какое-то добавочное эмпирическое содержание по сравнению с ее предшественницей, то есть предсказывает некоторые новые, ранее не известные факты. Будем считать, что теоретически прогрессивный ряд теорий является также и эмпирически прогрессивным..., если какая-то часть этого добавочного эмпирического содержания является подкрепленным, то есть если каждая новая теория ведет к действительному обнаружению новых фактов. Наконец, назовем сдвиг проблем прогрессивным, если он и теоретически, и эмпирически прогрессивен, и регрессивным - если нет"^[63].