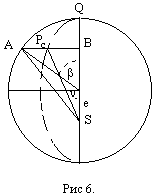
Итак, расстояние между планетой и Солнцем определяется уравнением
(3) 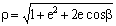 ,
,
получаемым, в соответствии с рис. 2 по закону косинусов. Наконец, из этого следует уравнение
(4)  ,
,
из которого по простому отношению косинусов выводится значение v, и, следовательно, положение планеты в момент времени t.
В этих рассуждениях используются: 1) закон радиуса, с помощью которого устанавливается отношение между временем и радиусом; 2) модификация теоремы Архимеда, посредством которой от вывода площади сектора круга, описываемого радиус-вектором, переходят к вычислению площади QSP, то есть чего-то совершенно отличного от сектора круга. Таким образом, отношение между временем и радиус-вектором преобразуется в отношение между временем и площадью круга. Едва ли можно говорить об эмпирических основаниях закона радиуса, а указанный переход от теоремы Архимеда к ее модификации не был обоснован математически. И то, и другое было хорошо известно Кеплеру. К этому надо добавить, что в уравнениях 1 - 4 фигурирует эксцентриситет e, что стало возможным только благодаря hypothesis vicaria, которые Кеплер вначале отвергал.
Таким образом, и на этой стадии исследований Кеплер вновь показал, что его не слишком заботила точность и достаточность эмпирического, математического или теоретического обоснования, хотя, как это видно из отрывка, приведенного в начале этой главы, их возможность им предполагалась. Поэтому нет ничего удивительного в том, что, исходя из минимума эмпирических данных, он в конечном счете отказался и от остававшейся части аксиомы Платона - от допущения о круговой форме планетарных орбит - как ранее он отказался от другой ее части, от допущения о постоянстве угловой скорости планет.
|
|
На этот шаг он решился в ходе новой попытки определить орбиту Марса. Вначале Кеплер применил уже описанный метод, использованный при вычислении орбиты Земли. Так же как тогда он сравнивал различные положения Земли по отношению к константному положению Марса, так и теперь три различных положения Марса соотносятся им с одним и тем же положением Земли. Тем самым были определены три расстояния Марса от Солнца и три угла, образуемых соответствующими радиус-векторами. С помощью утомительных, хотя и простых, тригонометрических вычислений он определил линию апсид и значение эксцентриситета Солнца для трех различных случаев. Все результаты были различны. Из этого мог быть сделан только один вывод: орбита Марса не может быть круговой.
Этот революционный для астрономии вывод был сделан на основе тех же смелых допущений, как и при вычислении орбиты Земли. Почва, на которой теперь стоял Кеплер, была не менее зыбкой, чем раньше: теория Тихо, hypothesis vicaria и вера в правильность данных Тихо.
И на заключительной стадии исследования, когда он пришел к заключению, что орбиты планет должны иметь форму эллипса, спекулятивный дух ему не изменил. Обратимся к рис. 3.
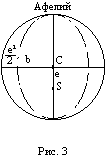
Прежде всего, следуя принципу простоты, Кеплер постулировал отклонение орбиты Марса от круговой формы по формуле b = 1-e2, где 1 - радиус, e - эксцентриситет Солнца, b - ось действительной орбиты. Позднее он представил b = 1 - (e2/2).
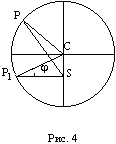
Но однажды он сделал открытие, суть которого мы сможем понять, взглянув на рис. 4, представляющий орбиту Марса. Он заметил, что
|
|
(5) 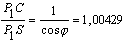 .
.
Здесь - наибольший угол, образованный схождением сегмента P1S (планета-Солнца) и P1C (планета-центральная точка окружности). Если затем просто подставить предполагаемое значение b в вычисления, то получится
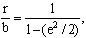
а поскольку e << 1, то
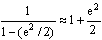 ,
,
но 1 + (e2/2) равно 1.00429, что согласуется с вычисленным результатом (5).
"Когда я увидел это, - писал Кеплер, - я словно бы очнулся ото сна и увидел свет"[49].
Полученное отношение, хотя оно было лишь приблизительным и верным только благодаря малости e, немедленно вдохновило его на новые спекуляции, представленные рис. 5.
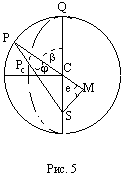
Он предположил, что (см. рис. 5) отношение, аналогичное уравнению (5) должно выглядеть следующим образом:
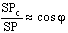 .
.
Иначе говоря, отношение расстояния между Солнцем и планетой на "истинной" орбите к расстоянию между Солнцем и планетой на "воображаемой" орбите аналогично отношению r/b на рис. 3.
При r = 1 получаем:
SP cos = PM
PM = 1 + e cos.
Из этого следует, что планетарные орбиты выражаются формулой
(6) 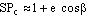
После изнурительных трудов - "paene usque ad insanium" - Кеплер установил, что уравнение (6) выражает формулу эллипса, хотя и приблизительно (надо напомнить, что математический аппарат, доступный Кеплеру, был еще достаточно примитивен).
Итак, и на этой стадии, как мы видим, Кеплер вновь прибегает к использованию предположений, спекуляций и грубых приближений; более того, проверка уравнения (6) предполагает сравнение значений SPe с теми значениями, которые были получены методами определения расстояния, применяемыми Кеплером; критические замечания об этих методах были сделаны выше.
В заключение рассмотрим еще один шаг Кеплера (см. рис. 6).