Логические схемы. Элементная база.

Логический вентиль (вентиль) – это своего рода элемент, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана, открывая или закрывая путь сигналам.

Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем, переключательных схем). Они воспроизводят функции полупроводниковых схем.

Логические функции отрицания, дизъюнкции и конъюнкции реализуют логические схемы, называемые инвертором, дизъюнктором и конъюнктором.

Логическая функция "инверсия", или отрицание, реализуется логической схемой (вентилем), называемой инвертор.

Дизъюнкцию реализует логическое устройство (вентиль) называемое дизьюнктор

Конъюнкцию 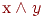реализует логическая схема (вентиль), называемая конъюнктором.

 

Пример. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в следующий разряд можно изобразить таблицей вида:

 

x	y	z	p

Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида

Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как или – если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 5.7):

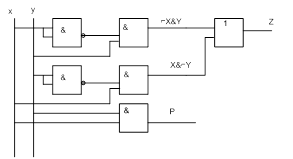
Рис. 5.8. Схема "черного ящика 1"

 

Алгоритмизация.

Алгоритм — это не просто набор конечного числа правил, задающих последовательность выполнения операций для решения задачи. Помимо этого, он имеет 5 важных особенностей:

· конечность;

· определенность;

· ввод;

· вывод.

· эффективность.

Порядок выполнения операций (старшинство операций – по убыванию) в языке С++:

1. Вычисление выражений в скобках;

2. Вычисление стандартных функций;

3. Умножение и деление (обозначаются "*" и "/");

4. Сложение и вычитание (обозначаются "+" и "–").

Рассмотрим базовые простые команды языка С++ [8-9].

1. Команда описания главной функции:

< тип > main ()

{

…

}

2. Команда описания неглавной функции:

< тип > <имя функции > (< передаваемые параметры>)

{

…

}

2. Ввод – команда ввода в рассмотрение (в тело алгоритма) тех или иных входных параметров:

cin >>вводимый параметр;

3. Вывод – команда вывода на экран тех или иных входных или выходных параметров алгоритма:

cout<< выводимый параметр;

4. Присваивание – команда изменения текущего значения переменной вида:

<идентификатор> = <выражение>;

5. Символ начала блок а {.

6. Символ конца блока }.

7. Команда вставки комментариев в текст алгоритма имеет вид:

/* комментарий в несколько строк */

// комментарий в одну строку

Различают три базовые алгоритмические структуры: следование, ветвление, повторение.

1. Действие следования состоит из двух команд с указанной очередностью их выполнения и имеет вид:

<команда – предшественник>;<команда – преемник>.

2. Структура типа ветвления в полной форме состоит из некоторого условия, проверяемого на истинность при выполнении структуры, команды, выполняемой при выполнении проверяемого условия, и команды, выполняемой при невыполнении условия. Условный оператор имеет вид

if <условие> <команда, выполняемая при выполнении условия>; else <команда, выполняемая при невыполнении условия>;

Структура повторения (цикл) служит для компактной записи одного и того же набора команд, повторяемых для различных значений параметров команд.

Структура повторения типа "пока (while)" записывается в виде:

while <условие продолжения повторения> <повторяемая команда>; for(<присваивание начального значения счетчику цикла>; <условие проверки выхода из цикла>; <изменение счетчика цикла>){ < операторы цикла>} 12. Булева алгебра. Функциональная полнота.

Определение. Алгеброй над множеством логических функций с двумя бинарными операциями, обозначаемыми как логическое умножение & и логическое сложение v и одной унарной операцией (отрицанием)

Ø называется булевой алгеброй. Будем обозначать ее символом S_B.

Свойства булевой алгебры.

Замкнутость

для " A и B Î S_B

A v B Î S_B

A & B Î S_B

Коммутативность

A & B = B & A

A v B = B v A

3. Ассоциативность

A v (B v C) = (A v B) v C

Дистрибутивность

A & (B v C) = (A & B) v (A & C)

A v (B & C) = (A v B) & (A v C)

Идемпотентность

A v A = A & A = A.

6. Булева алгебра содержит элементы 0,1, такие что для всякого

элемента A Î S_B справедливо:

A v 0 = A, A v 1 = 1

A & 0 = 0, A & 1 = A.

7. Для каждого элемента A Î S_B существует элемент , такой что

A v =1

A & =0.

 

Закон поглощения

A & (A v B) = A v A & B = A.

Закон Де Моргана

 

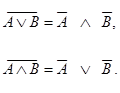
Определение. Система функций f₁, f₂... f_n Î S_B называется полной, если любая функция j из S_B представима в виде суперпозиции функций f₁, f₂... f_n.

Определение. Система функций f₁, f₂... f_n Î S_B, являющаяся полной, называется базисом.

Определение. Минимальным базисом называется базис, для которого удаление хотя бы одной из функций f_i превращает систему функций в неполную.

Определение. Алгебра над множеством логических функций с двумя бинарными операциями & и Å называется алгеброй Жегалкина.