ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

 

 

Расчет надежности технологических процессов в зависимости от поставленной задачи может преследовать следующие цели:

1. Определение надежности выполнения задания по одному показателю качества. Задача сводится к расчету вероятности то­го, что изготавливаемая продукция по одному определенному параметру будет соответствовать требованиям технической доку­ментации.

. 2. Определение надежности выполнения задания по всей со­вокупности нормируемых показателей качества. Задача сводится к расчету вероятности того, что технологический процесс обес­печит изготовление продукции в соответствии, с требованиями ее технической документации по всем показателям качества изго­тавливаемой продукции.

3. Расчет вероятности выполнения задания по параметрам производительности. В этом случае производится расчёт вероятности выполнения задания только по параметрам производительности.

 

Рис. 48. Последовательная технологи- Рис. 49. Параллельная техноло- ческая цепь (О — операция) гическая цепь (О — операция)

 

Расчет надежности выполнения задания по одному показате­лю качества продукции. Вероятность выполнения задания по па­раметру y(t) обеспечивается, если на каждой из последователь­ных или параллельных операций (рис. 48 и 49) выполняется условие:

 

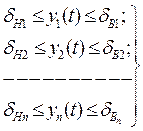, (1)

где δ_Н1; δ_Н2; …; δ_Нn; δ_В1; δ_В2; …; δ_Вn – нижние и верхние границы допуска на нормируемый показатель

 

Вероятность выполнения задания по параметру y(t):

 

Р(δ_Н) ≤ y(t) ≤ δ_В = Р₁(t). (2)

 

Пусть определены вероятности выполнения неравенств (1), т.е.:

 

(3)

 

Если не выполнено хотя бы одно из неравенств (3), то не выполняется и неравенство (2).

Искомая вероятность:

 

(4)

 

Вероятность отказа:

 

(5)

 

Если F(t) ≤ 0,2, то расчёт можно вести по более простой формуле:

 

(6)

где F_i (t) – вероятность отказа на каждой операции.

 

При этом время восстановления не учитывается. Моменты отказов формируют поток, называемый потоком отказов. В качестве характеристики потока отказов используется «ведущая функция» Q(t) данного потока — математическое ожидание чис­ла отказов за время t:

Ω(t) = Mr(t), (7)

 

где r(t) – число отказов за время t.

 

Математическое ожидание числа отказов за интервал времени (t₁, t₂) определяется по формуле:

Mr (t₁, t₂) = Ω (t₂) - Ω (t₁), (8)

 

где r(t) – число отказов за время (t₁, t₂).

 

На основе этого легко определить параметр потока отказов – он представляет собой функцию:

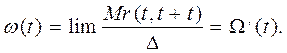(9)

 

Допускается вычисление параметра потока отказов по приближенной формуле:

(11)

 

Для ординарных потоков без последствия параметр потока отказов связан с ведущей функцией соотношением:

(12)

 

Статистическая оценка х среднего срока функционирования определяется по формуле:

(13)

Рисунок 1 – Шестерня с хвостовиком

Пример 1. Рассмотрим технологический процесс обработки шестерни с хвостовиком (рис. 50). За выходной показатель качества примем шерохова­тость опорной поверхности диаметр 0 60, Ra= 1,0ч÷1,25 мкм.

Технологический процесс состоит из трех операций: токарной, термиче­ской и шлифовальной. Параметр Ra будет находиться в пределах 1,00<у(t)==Ra ≤ l,25, если выдержаны размеры на каждой операции.

По результатам статистической обработки данных по технологическим операциям определены величины Pi(t) и Fi(t): P1(t)=0,90; P2(t)=0,75; P3(t)=0,95 и соответственно Ft(f) =0,10; Ft(t)=0,25; F3(t)=0,05. Тогда вероятность выполнения задания по исследуемому показателю качества опре­делится по формуле (4). Вероятность отказа определяется по формуле (6). Параметр потока отказов ω(t) вычисляется по приближенному урав­нению (8). Для определения величины ω(t) необходимо проанализировать обработку достаточно представительной выборки исследуемой детали. Резуль­таты анализа одной из трех выборок по 150 каждая приведены в таблице 1.

 

Таблица 1

 

выборка	Δt = Tn – Tn-1	n	N	ω(t)
	0 - 20 20 - 40 40 - 60			0,0057 0,0125 0,0049

 

 

По полученным значениям ω(t) построен график изменения параметра потока отказов по операциям (рисунок 2). Средний срок функционирования tср определяется экспериментально.

Расчеты показывают, что наибольшее число отказов и низкая работо­способность возникает при термической обработке. Это обусловливает невы­сокую надежность всего технологического процесса по контролируемому пока­зателю качества.

Разберем простейший случай, когда регрессия выходного параметра у но входному параметру х прямолинейна, а условная дисперсия D(y/x)

y = a + bx, (14)

 

D(y) = D(y) x + b² D(x), (15)

 

где у – средняя величина выходной погрешности;

bx – величина, пропорциональная средней выходной погрешности х;

a – константа, постоянная относительно x;

b² D(x) – величина, пропорциональная входной дисперсии D(x);

D(y/x) – условная дисперсия, постоянная относительно D(x).

 

Рисунок 2 – Зависимость параметра потока отказов от надёжности на отдельных операциях 0

 

Используя выражения (14) и (15), можно выяснить, как изменяются средняя величина у и дисперсия D(y), относящиеся к выходному показателю качества, при изменении входных характеристик. Величина bх характеризует ту часть погрешности у, которая была перенесена из предыдущей операции; при этом коэффициент b является коэффициентом переноса погрешностей. Величина а соответствует собственной погрешности операции. Она может быть как положительной, так и отрицательной и соответственно увеличивает или уменьшает выходную погрешность на одну и ту же величину.

Постоянную составляющую можно компенсировать, так как она прояв­ляется в смещении центра группирования погрешностей, являющихся следст­вием смещения уровня настройки станка в процессе обработки.

Показатели, входящие в формулы (14) и (15), могут быть рассчитаны на ЭВМ по программе корреляционного анализа для одномерных объек­тов.

Теперь рассмотрим технологический процесс, состоящий из ряда операций (рисунок 3). Входными параметрами являются величины хо, xi..., x_n-1, выход­ной параметр х_n характеризует качество готовой детали. Если принять, что плотности вероятности распределения случайных величин х₀, x₁, x₂…х_n-1, х_n нормальны, то можно считать их совместную плотность также нормальной. Соответственно множественные и парные регрессии линейны.

 

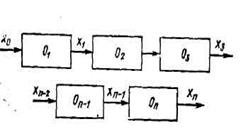
Рисунок 3 – Технологическая цепь (0 – операция)

 

Примем, что по ходу технологического процесса на надежность после­дующего вида обработки влияют лишь погрешности, внесенные предыдущей операцией. Условное математическое ожидание выхода:

 

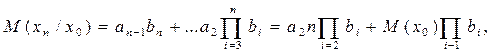(16)

 

где

a_i = M(x_i) + b_i M(x_i-1);

(17)

 

Дисперсия выхода качества:

(18)

где

D(x_i-1) = D(x_i) (1-r² x_i / x_i-1),(19)

 

(здесь r² x_i / x_i-1 - коэффициент корреляции).

 

Пример 2. Определим числовые параметры технологического процесса обработки детали, приведенного в примере 1.

При исследовании выборок порядок изменения заранее пронумерованных деталей оставался одинаковым на всех операциях. Информация о технологическом процессе экспериментальных данных состояла из трех массивов в соот­ветствии с последовательностью операций.

Вычисления величин М(х), D(x) производились по формулам (15-18). Полученные числовые характеристики технологического процесса обра­ботки исследуемой поверхности (диаметр 60 Ra = 1,0÷1,25) приведены в таблице 2.

Таблица 2 – параметры технологического процесса обработки опорной поверхности детали “шестерня с хвостовиком”

 

Наименование операции	ООбозна- ччение	Математи- ческое ожидание	Среднее квадратическое отклонение σ(х)	ДДиспер- ссия D(x)	Коэффициент корреляции ri, i-1	Коэффици- енты регрессии
	мкм	a	b
Токарная Термическая Шлифовальная	X Y z	2,35 2,40 1,25	0,0075 0,0087 0,0070	0,00056 0,184 0,0049	0,184 0,687	- 0,014 0,032	- 0,76 0,64

Расчет надежности выполнения технологического процесса по всем нормируемым показателям качества. Рассмотрим общий случай, когда после технологического процесса нормируется раз­личное число показателей, значения которых попарно независи­мы. Часть этих показателей контролируется (рисунок 4).

Положим, что для операций О₁..., O_j,..., О_n нормируется соответственно a, b, f параметров. Из них b',..., d',..., i' конт­ролируется.

Считаем, что отказа нет, если ни на одной операции, ни один из параметров не выходит за границы допуска. Тогда вероят­ность выполнения задания по параметрам качества будет

(20)

где

A = (a - b') + … + (c - d') + (f - i');

B = b' + … + d' + … + i';

P_i(t); P_i(t) – вероятности выполнения задания по показателям качества.

Вероятность отказа:

(20)

Характеристики величин ω(t) и t_ср для общего случая опреде­ляются по формулам (9) и (11).

Как следует из выражений (13) и (14), все необходимые данные для расчета числовых параметров могут быть получены в результате использования программы регрессионного анализа. К ним относятся значения свободных членов уравнений регрес­сии d, характеризующих постоянную составляющую суммарной погрешности; коэффициентов регрессии b_i характеризующих слу­чайную составляющую суммарной погрешности; статистических характеристик М(х), D(x) каждой операции; коэффициентов парной и множественной корреляции r_i/i-1, R_i/i-1.

Приведенная в первом разделе этого параграфа схема явля­ется частным случаем расчета надежности технологического про­цесса.

Более общий случай представляется зависимостями выход­ных нормируемых показателей качества от погрешностей на всех технологических операциях. Выражениями для характеристик выходного качества будут [37]:

условное математическое ожидание:

a_i(i = 0,1, …, n-1), (21)

 

где d_i – коэффициенты множественной регрессии;

 

Дисперсия выходных признаков качества может быть предо­ставлена в виде двух слагаемых, соответствующих действию учи­тываемых и неучитываемых факторов:

D(x_n)=D_l(x_n/x_n-1,...,x₀) + D₂(x_n/x_n-1, …, х_о), (22)

где

(23)

Все эти параметры могут быть получены после корреляцион­но-регрессионного анализа.

На качество поверхностей готовых деталей влияют не только геометрические параметры заготовок, но и характеристики си­стемы СПИД

(жесткость системы, режимы резания, износ инст­румента и т. д.).

На рисунке 4 представлен технологический процесс, состоящий из многомерных операций. На входе технологического про­цесса действует С случайных величин x₀ⁱ (i ≠ 0) (i = l, 2,... С), а выход первой операции имеет D случайных величин x_i(i) (j = 1, 2,..., d), являющихся входами для второй технологической операции, и т. д.

Выход всего технологического процесса характеризуется слу­чайными величинами. Математическое ожидание любого из вы­ходов по всем входам на основании уравнения регресси (24)

 

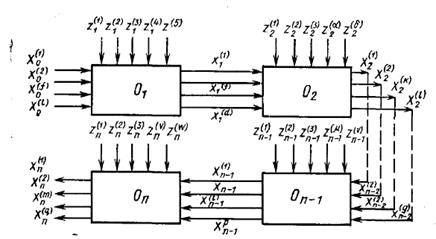
Рисунок 4 – Структурная схема многомерного технологического процесса (0 – операция)

Суммарную дисперсию любого из параметров на выходе сле­дует рассматривать состоящей из двух условных дисперсий, од­на из которых определяется влиянием входов х₀,..., х_n-1,..., z₁, …, z_n другая D₂ — неучтенными факторами:

 

D(x_n) = D₁(x_n/x₀, …, x_n-1; z₁, …, z_n) +

+D₂(x_n/x₀, …, x_n-1; z₁, …, z_n). (25)

 

Первая из условных дисперсий

 

D₁(x_n^m/x₀, …, x_n-1; z₁, …, z_n) = D(x_n^m) (1-R²x+n) x₀, …, x_n-1; z₁, …, z_n. (26)

 

Вторая условная дисперсия может быть определена из усло­вий влияния и взаимосвязи всех случайных величин.

Однако такой вариант, как показали исследования [37], не всегда рационален, так как связи параметров заготовок меж­ду собой и с параметрами обработки зачастую малозначимы.

Условная дисперсия при независимости указанных выше слу­чайных величин

D₁(x_n^m/x₀, …, x_n-1; z₁, …, z_n) =

(27)

Были определены показатели надежности технологических процессов типовых деталей (корпусов, шестерен, валов и др.) по основным параметрам качества, установленным техническими требованиями на их изготовление.

Результаты расчета приведены в таблице 4.

Развернутая методика расчета показателей надежности тех­нологических процессов при обеспечении заданных характери­стик поверхностей деталей машин. Определение показателей на­дежности технологического процесса производится на основе анализов конструкторской документации технологического про­цесса обработки; имеющейся статистики по уровню брака на отдельных операциях; данных об отказах деталей при приемо­сдаточных испытаниях и эксплуатации машин; теоретического анализа точности обработки; анализа геометрической точности технологического оборудования.

На указанной основе устанавливаются числовые значения показателей надежности технологического процесса, кроме па­раметров, которые оговорены техническими условиями на изго­товление. При расчете надежности должны учитывать и те па­раметры получаемого изделия, которые не указаны в чертеже и ТУ. Имеются в виду не пропуски в чертежах, т. е. явный брак, а те параметры, нормирование которых чертежом, по мнению конструктора, либо не оказывает существенного влияния на экс­плуатационные свойства изделия, либо их трудно контролиро­вать и получать в производственных условиях.

В таблице 5 приведены некоторые из параметров которые в чертежах часто опускаются.

Многие из перечисленных параметров оказывают существен­ное влияние на эксплуатационные свойства изделий и тем са­мым на показатели надежности.

Особенно большое число неучтенных параметров относится к характеристикам поверхностного слоя. Поверхность деталей машин имеет сложное строение и для полного ее описания тре­буется значительное количество параметров. Обычно многие из них в конструкторской документации не нормируются.

Зависимость отдельных эксплуатационных свойств, характе­ризующих работоспособность изделий J_i, от параметров, число­вые значения которых не оговариваются чертежом и ТУ, ω, может быть представлена системой уравнении:

J₁ = f₁ (b, ω₁, ω₂, …, ω_n);

J₂ = f₂ (b, ω₁, ω₂, …, ω_m (28)

I_n = f_n (b, ω₁ⁱ, ω₂ⁱ, …, ω_mⁱ).

где b – совокупность параметров, заданных чертежом.

 

В первом приближении каждая из функций f_i может быть представлена в виде произведения (или суммы) функций:

(29)

 

 

Таблица 4 – Количественные показатели надёжности технологических процессов при обеспечении основных показателей

Деталь	Контролируемый параметр	Показатели надёжности
P (t)	F (t)	ω (t)
Корпусы     Зубчатые колёса     Валы и оси     Муфты     Втулки	Шероховатость:   базовых поверхностей Ra < 2,5 мкм внутренних цилиндрических поверхностей посадочных отверстий Ra < 1,25 мкм Смещение отверстий Δ = 0,10÷0,15   Шероховатость рабочих поверхностей, Ra = 1,25÷2,5 мкм Твёрдость HRC 55 – 60 Биение зубчатого венца δ = 0,08÷0,12 (Пятно контакта)   Шероховатость опорных поверхностей Ra = 1,25÷2,5мкм   Твёрдость HRC 50 -55   Взаимное биение δ = 0,15÷0,20   Шероховатость: внутренних посадочных цилиндрических поверхностей Ra < 2,5 мкм   Сопрягаемых поверхностей Ra=1,25÷2,5   Шероховатость посадочных поверхностей Ra <2,5 мкм   Взаимное биение наружных и внутренних цилиндрических поверхностей δ = 0,10	0,90   0,85     0,80     0,95     0,85 0,80     0,90   0,85   0,85   0,85   0,80     0,85     0,75	0,02   0,02     0,03     0,01     0,03 0,03     0,02   0,03   0,03   0,02   0,03     0,03     0,04	0,003   0,003     0,004     0,002     0,004 0,005     0,003   0,004   0,004   0,003   0,004     0,004     0,006

 

Таблица 5 – Дополнительные параметры, опускаемые в чертежах и оказывающие влияние на эксплуатационные свойства деталей машин

 

Наименование параметра	Примеры параметров, не приводимых в чертежах и ТУ	Эксплуатационные свойства, на которые оказывает влияние данный параметр
Размеры     Требования к материалу     Остаточные напряжения     Наклёп     Шероховатость поверхности   Макрогеометрия     Прочие параметры	Радиусы скруглений и остроты кромок   Вид термообработки; карбидная неоднородность   Величина остаточных напряжений 2-го и 3-го родов Направление действия напряжения 1-го рода   Интенсивность наклёпа; степень однородности наклёпа   Форма микронеровностей   Допуски на погрешности формы по отдельным поверхностям и для взаимосвязи поверхностей   Допустимая величина заусенцев и сколов. Степень загрязнённости поверхностей перед сборкой	Усталостная прочность; точность работы гидросистем   Износостойкость; Прочность   Усталая прочность; износостойкость; коробление   Износостойкость; магнитные свойства     Коэффициент трения; контактная жёсткость Контактная жёсткость, повышенный износ в период приработки     Износостойкость; безотказность гидросистем

 

Теоретически число сомножителей в выражении (174) равно бесконечности. Но на практике лишь некоторые из них существенно отличны от единицы при изменении от max до min:

 

Δω_j = ω_jmax – ω_jmin. (30)

 

Величина Δ_ωi определяется из конкретных условий работы изделия и технологии изготовления

Δf_i = Δf_i1 + … + Δf_in = 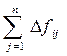. (31)

 

Из огромного числа значений Δf_i1 только несколько сущест­венно отличны от нуля при изменениях ω_j в пределах, характер­ных для технологии изготовления, конструкции и эксплуатации изделия. Задаваясь некоторой величиной z, разбиваем множе­ство параметров, не учтенных чертежом, на две группы. В пер­вую отнесем все параметры, которые существенно влияют на заданные характеристики поверхностей изделия (Δf ≥ z), а в другую — параметры, не оказывающие существенного влияния на эти характеристики.

Конкретное значение z определяется исходя из анализа ра­боты изделия и технических условий на него.

В качестве примера рассмотрим параметры, которые оказы­вают влияние на контактную жесткость плоского неподвижного стыка и которые зависят от технологии (таблица 5).

Если для условий таблицы 5 принять 2=10%, то факторами, зависящими от технологического процесса, будут параметры 2, 3, 8 и, частично, 6. Суммарное их влияние может быть оценено величиной 60—70%, т. е. в данном случае в зависимости от тех­нологии изготовления жесткость стыка может меняться почти в 2 раза при полном выполнении всех требований чертежа.

В зависимости от того, ведется ли расчет надежности техно­логического процесса по одному показателю качества или по всем нормируемым показателям, для определения P(t), F(t), ω(t) используются соответственно формулы (4) – (9), (12) – (21), (21 – 26).

Таблица 5 – Параметры, влияющие на жёсткость стыка

 

 

Параметры	Регламентируется ли конструкторской документацией	Примерное максимальное значение Δfi /J·100%
1. Максимальная высота микронеровностей 2. Форма микро- неровностей 3. Форма вершин микро- неровностей 4.Высота макро- геометрических неровностей 5.Взаимное расположение микронеровностей на контактируемых поверхностях 6. Наклёп поверхностного слоя 7. Загрязнение поверхностного слоя 8. Наличие отдельных микровыступов, значительно превосходящее среднее 9. Остаточные напряжения	Регламентируется   Не регламентируется   >>   Регламентируется косвенно в виде числа пятен при шабрении Не регламентируется   >>   >>   >>   >>	30,0   15,0   10,0   15,0     25,0   5,0   5,0   3,0   1,0

 

 

Расчет следует выполнять последовательно по операциям технологического процесса или таблично-аналитическим ме­тодом.

Таблица заполняется для всех операций обработки данной поверхности. Для каждой операции выписываются все парамет­ры, которые должны быть получены в результате ее выполнения. Источниками информации для установления значений P(t), ω(t) являются статистический материал по браку данной или аналогичной деталей; расчеты по определению вероятности по по­лучения брака в зависимости от соотношения показателей; значения показателей надежности на изделие.

 

КЛАССИФИКАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ПО СТЕПЕНИ ИХ НАДЕЖНОСТИ

 

 

Оценка надежности технологических процессов производит­ся при помощи показателей P(t), F(t), ω(t) и tср. Для удобства сравнения технологических процессов и в целях унификации в методических указаниях ВНИИНМАШ рекомендовано весь диа­пазон изменений величин принятых показателей разбить на классы и разряды.

Предлагаемая классификация состоит из восьми классов на­дежности, каждый из которых состоит из трех разрядов. В ее основу положен геометрический ряд прогрессии вероятности от­каза технологического процесса F(t). Знаменатель прогрессии 10. Общий диапазон изменения F(t) —от 10⁷ до 1,0.

Соответствующие числовые значения с разбивкой на классы приведены в таблице 7.

Рассматриваемый диапазон (10⁷—1,0) перекрывает всю об­ласть F(t), которые характерны для современной технологии производства. Наиболее высокий класс надежности I соответст­вует технологическим процессам изготовления изделий высшей степени качества, а последний VIII—технологическим процес­сам с высоким уровнем брака получаемой продукции.

Для технических процессов общего машиностроения наибо­лее характерными являются классы IV, V, VI.

Основным показателем, на базе которого следует относить реальный технологический процесс к тому или иному классу, яв­ляется показатель F* (t) —вероятность получения «просочивше­гося» брака в готовом изделии в расчете на один нормируемый показатель. В упрощенном варианте, если известны величи­на F(t),

 

F*(t)=[l—F(t)]^1/n (33)

 

где n — общее число нормируемых показателей.

Кроме вероятности отказа F(t) каждому классу техпроцесса можно

предпослать и величину вероятности безотказного функ­ционирования P(t) (см. таблицу 6). Зависимость величин F(t) и P(t) можно представить и графически (рисунок 7).

Предлагаемая классификация позволит сравнивать техноло­гические процессы по степени их надежности и регламентировать

показатели надежности в конструкторской и технологической документации такими образом, определение количественных показателей на­дежности позволяет с вероятностной точки зрения оценить воз­можность обеспечения назначаемыми технологическими процес­сами характеристик качества поверхностей как регламентирован­ных технической документацией, так и не регламентированных ею с целью обеспечения необходимых эксплуатационных свойств деталей машин с учетом технологической наследствен­ности.

 

Рисунок 7 – График классификации значений показателей надёжности в зависимости от класса технологического процесса

 

 

 

ПРАКТИЧЕСКАЯ РАБОТА№6