ОПРЕДЕЛЕНИЕ комплексных показателей надежности технических систем

ИНСТИТУТ СФЕРЫОБСЛУЖИВАНИЯ И ПРЕДПРИНИМАТЕЛЬСТВА (ФИЛИАЛ)

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

В Г.ШАХТЫРОСТОВСКОЙ ОБЛАСТИ

(ИСОиП (ФИЛИАЛ) ДГТУ)

 

 

Кафедра Технические системы ЖКХ и сферы услуг

Журнал ущен к защите

(подпись, дата)

 

 

ЖУРНАЛ

практических работ

 

 

по дисциплине Основы теории надежности и диагностики технических систем

Подробно материалы отчета размещены на рабочем столе монитора компьютера № Т000013253

Выполнил Наумов К.В.

(подпись) (инициалы, фамилия)

группа ТМО Рb-31

Проверил Першин В.А.

(подпись, ученая степень, звание) (инициалы, фамилия)

 

Оглавление

ПРАКТИЧЕСКАЯ РАБОТА №1 2

ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ ПОЯВЛЕНИЯ 2

СОБЫТИЙ В ТЕОРИИ НАДЕЖНОСТИ 2

ПРАКТИЧЕСКАЯ РАБОТА №2 4

ОБЩИЕ МЕТОДЫРАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ МАШИН В ПЕРИОД НОРМАЛЬНОЙ ЭКСПЛУАТЦИИ 4

ПРАКТИЧЕСКАЯ РАБОТА №3 6

ОПРЕДЕЛЕНИЕ КОМПЛЕКСНЫХ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ 6

ПРАКТИЧЕСКАЯ РАБОТА №4 10

ОБРАБОТКА РЕЗЛЬТАТОВ НАБЛЮДЕНИЯ О НАДЕЖНОСТИ МАШИН 10

ПРАКТИЧЕСКАЯ РАБОТА №5 17

МЕТОДИКА РАСЧЁТА И ИССЛЕДОВАНИЯ НАДЁЖНОСТИ 17

ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ 17

ПРАКТИЧЕСКАЯ РАБОТА№6 33

ИСПЫТАНИЕ ХОЛОДИЛЬНОГО ПРИБОРА 33

 

 

ПРАКТИЧЕСКАЯ РАБОТА №1

ОПРЕДЕЛЕНИЕ вероятности ПОЯВЛЕНИЯ

СобытиЙ в теории надежности

 

Цель работы: получить навыки определения показателей проявления вероятности совместных и несовместных событий

Расчеты показателей проявления
вероятности событий

Задача №1.

При испытаниях на надежность группы невосстанавливаемых изделий время испытаний разбито на четыре периода. Установлено, что вероятность отказа в период Т₁ составила 0,4,период Т₂ – 0,2,в период Т₃ – 0,1,в период Т₄ = 0,3.

Найти вероятность того, что наугад взятое изделие из группы отказало

1. либо в первый, либо в третий периоды времени,

2. либо во второй или третий периоды испытаний.

Решение

Так как отказы изделий в различные периоды испытания есть события несовместимые (отказ изделия в какой – либо период исключает его отказ в другой период), то теорема сложения вероятностей применима. Поэтому искомая вероятность равна

1. Р(Т₁ + Т₃) = 0,4+0,1=0,5,

2. Р(Т₂ + Т₃) = 0,2+0,1=0,3.

Задача №2

По статистике из всех работ по ТО гидросистем мусоровозов 50%пиходится на гидропривод рабочих органов, 75% на механическую систему рабочих органов. Какова вероятность того, что очередной мусоровоз поступивший для ТО гидросистемы, будет требовать проведения работ по ТО гидропросистемы, либо только в системе гидропривода, либо по механической системе?

Решение.

События, заключающиеся в необходимости проведения работ по ТО гидропривода и гидросистемы, являются независимыми друг от друга и совместными событиями

1. Вероятность проведения работ по ТО гидропривода

Р(А) =50/100 = 0,5

2. Вероятность проведения работ по ТО механической системы Р(В) =75/100 = 0,75

3. Вероятность того, что мусоровоз будет требовать работ по ТО обеих систем

Р(А×В) =0,5×0,75=0,375

4. Вероятность того, что мусоровоз будет требовать работ по ТО какой – либо одной из систем

Р(А + В) = 0,5+0,75-0,375=0,875

Практическая часть

1. Изучить методические указания и получить задание.

2. Рассчитать требуемые показатели надёжности

3. Оформить отчёт о практической работе

4. Защититить отчёт о практической работе при собеседовании с преподавателем

Исходные данные по вариантам

Показатель	Вариант
Задача №1
Р(Т1 )	0,1	0,55	0,45	0,3	0,55	0,35	0,4	0,15	0,2	0,5
Р(Т2 )	0,3	0,05	0,1	0,1	0,25	0,1	0,2	0,55	0,35	0,17
Р(Т3 )	0,2	0,15	0,05	0,4	0,05	0,15	0,1	0,05	0,4	0,2
Р(Т4 )	0,4	0,25	0,4	0,2	0,15	0,4	0,3	0,25	0,05	0,12
Задача №2.
P (А)
P (В)

 

Отчёт должен содержать

1.Цель работы

2.Задание

3.Основные положения и формулы

4. Расчеты

5. Выводы по работе

 

 

Практическая работа №2

Общие методы расчета показателей надежности машин в Период нормальной эксплуатации

Цель работы: получить навыки определение количественных значений показателей надежности с использованием теорем теории вероятности

Расчеты показателей надежности

Задача №1

Определить показатели безотказности шарикового подшипника при наработке 600 часов и 80% ресурсе изделия, если известно, что наработка изделия подчиняется экспоненциальному закону с интенсивностью отказов l = 5·10 ^–4 час ^-1

Решение

1. Определяем вероятность безотказной работы для наработки 500 часов

P (t) = e ^{–l t} = e ^{– 0,0005×600} = e ^–0,25 = 0,77880

2. Определяем вероятность отказа при наработке 600 часов

Q(t) = 1 – P(t) = 1 – 0,7788 = 0,2212

3. Определяем среднюю наработку до отказа изделия

T = 1 / l = 1 / 5·10 ^–4 = 2000 час

4. Определяем 80% ресурс изделия

P (t) = e ^{–l t} = 0,8

–l t = ln 0,8,

t = – (ln 0,8 / l) = –(– 0,223 / 0,0005) = 446 час

Задача №2

Определить показатели безотказности невосстанавливаемого изделия при наработке 1000 часов, если известно, что наработка изделия подчиняется экспоненциальному закону, а 80% ресурс изделия соответствует наработке в 500 часов. Установить технический ресурс изделия.

Решение

1. Определяем интенсивность отказов изделия

P (t) = e ^{–l t} = 0,8

– l 500 = ln 0,8,

l = – (– 0,223 / 500) = 0,00045

2. Определяем среднее время безотказной работы

T = 1 / l = 1 / 4,5·10 ^{– 4} = 2222,2 час

3. Определяем технический ресурс изделия.

Так как изделие – невосстанавливаемое, то технический ресурс равен среднему времени безотказной работы

Т_Р = Т = 2222,2 час

4. Определяем вероятность отказа изделия при наработке 1000 часов

Q(t₀) = Q(0, t₀) = P(t < t₀) = 1 – P(t₀) = 1 – e ^{– l t} =
= 1– e ^{–l× 1000} = 1 – e ^{–0,00045×1000} =1 – 0,437 = 0,563

Задача №3

Определить показатели безотказности невосстанавливаемого изделия при наработке 500 часов и 50% ресурсе изделия, если известно, что наработка изделия подчиняется экспоненциальному закону со средней наработкой до отказа 2000 час

Решение

1. Определяем интенсивность отказов изделия

l = 1 / Т = 1 / 4000 = 5·10 ^–4час^–1

2. Определяем вероятность безотказной работы для наработки 500 часов

P(t) = e ^{– l t} = e ^{– 0,0005×500} = e ^{– 0,25} = 0,7788

3. Определяем вероятность отказа при наработке 500 часов

Q(t₀) = Q(0, t₀) = P(t < t₀) = 1 – P(t₀) = 1 – 0,7788 = 0,2212

4. Определяем 80% ресурс изделия

P(t) = e ^{– l t} = 0,5;

–l·t = ln 0,5,

t = – (ln 0,5/ l) = – (– 0,693 / 0,0005) = 1386,3 час.

 

 

 

РАБОТА №3

ОПРЕДЕЛЕНИЕ комплексных показателей надежности технических систем

Цель работы: получить навыки определения количественных значений комплексных показателей надежности в период нормальной эксплуатации объекта

Расчет комплексных показателей надежности
в период нормальной эксплуатации объекта

Задача №1

Определить среднюю наработку на отказ, среднее время восстановления работоспособности, коэффициент готовности восстанавливаемого изделия, коэффициент ремонтопригодности и коэффициент технического использования, если известно следующее:

- наработка подчиняется экспоненциальному закону распределения;

- за период наблюдения получены данные, представленные в таблице

-

Период наблюдения, K i	Поток отказов, wi	Количество отказов, N	Время восстановления i-го отказа ТВ, час
	9·10 -3
	8·10 -3
	4·10-3

- время технического обслуживания изделия составляет 10% от среднего времени восстановления.

Решение

1. Определяем среднюю за период наблюдения величину потока отказов

w_СР= å w_i / N = (9·10 ^–3 /8+ 8·10 ^–3 /4+ 4·10^-3/7) / 3= 1,23·10 ^–3

2. Определяем среднюю наработку на отказ

Т_Н = 1 / w = 1 / (1,23·10 ^–3) = 813 час

3. Определяем среднее время восстановления работоспособности

Т_В = å Т_Вi / å n _i = (27 + 22 + 17) / (8 + 4 + 7) = 3,47 час.

4. Определяем коэффициент готовности изделия

К_Г = 1 / (1 + w×Т_В) = 1 / (1 + 4,66*10 ^–3×3,45) = 0,5

5. Определяем коэффициент ремонтопригодности изделия

К_Р = 1 – К_Г = 1 – 0,5 = 0,5

6. Определяем коэффициент технического использования

Т_ТО = 0,1 Т_В = 0,1 ×3,45 = 0,345

К_ТЕХ = Т_Н / (Т_Н + Т_В + Т_ТО) = 213 / (213 + 3,45 + 0,345) = 0,93

 

Задача №2

На основании заданных рядов наработки и времени восста­новления определить количественные значения показателей надежности гидросистемы снегоуборочной машины: среднюю наработку на отказ, среднее время восстановления, вероятность безотказной работы, вероятность восстановления, коэффициент готовности.

Решение

1. Определяем среднюю наработку и среднее время вос­становления (ч)

V_ср = и Т_ср = .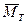

где и 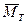- соответственно математическое ожидание ряда наработки и ряда восстановления. Для их определения произведем обработку статистических рядов наработки и времени восстановле­ния.

Строим интервальный вариационный ряд, разбивая ряды случай­ных величин наработки и времени восстановления на разряды.

Величину интервала определяем по формуле Стэрджеса:

,

где x _max и x _min соответственно максимальная и минимальная величины в полученном статистическом ряде;.; ∑n_i - число слу­чайных величин данного ряда.

Далее определяем представителя для каждого разряда N_i, который является средним значением интервала разряда и опреде­ляем количество попаданий n_i. случайных величин наработок и времени восстановления в каждый интервал разряда.

Определяем частость появления в каждом интервале разряда случайных величин наработок и времени восстановления по формуле:

,

где n_i - количество попаданий в разряд; ∑n_i - сумма случайных величин данного ряда.

Данные заносим в табл. 1.2.

Таблица 1- Результаты обработки статистических рядов
наработки и времени восстановления

№ п/п	Интервалы раз­рядов	Представитель разряда	Кол-во попада­ний в разряд	Частость появ­ления в разряде
hопт	Ni	ni	Pi
V	T	V	Т	V	Т	V	T

 

Определяем математическое время ожидания для ряда нара­боток и времени восстановления согласно табличных данных по формуле:

,

где N_i - представитель разряда; Р_i - частость появления в разделе случайных величин наработки и времени восстановления.

2. Произвести построение графика зависимости вероятности безотказной работа Р_без от наработки V (рис.1).

Для этого необходимо определить 6-7 точек значений вероятности безотказной работы Р_без в зависимости от наработки сог­ласно экспоненциальному закону распределения случайных величин по формуле:

,

где V - наработка машины от ее включения до первого от­каза;

ν - наработка машины, ч;

λ₁ - интенсивность отказов, .

Значения наработки брать произвольно, от нуля до тех пор, пока вероятность безотказной работы не примет значение 0,01-0,05.

3. Произвести построение графика зависимости вероят­ности восстановления Р_B от времени восстановления.

Построение ведется согласно предыдущему пункту, только ве­роятность восстановления определяется по формуле:

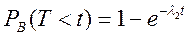
и значения времени восстановления берутся от нуля до тех пор, пока вероятность восстановления не примет значение 0,9-0,95 (рис. 2)

 

Рис.1. График зависимости вероятности безотказной работы от наработки

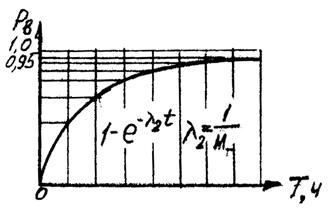Рис. 2 График зависимости вероятности восстановления от времени восстановления.

4. Определить коэффициент готовности по формуле:

К_г = T/(T + T_ср),,

где Т - среднее время наработки на отказ машины;

Т_ср - среднее время восстановления машины.

 

ПРАКТИЧЕСКАЯ РАБОТА №4