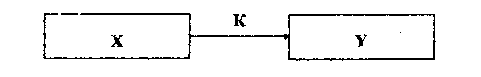
Известна производительность источника информации H1(X) т.е. среднее количество двоичных единиц информации, поступающее от источника в единицу времени (численно оно равно средней энтропии сообщения, производимого источником в единицу времени). Пусть, кроме того, известна пропускная способность канала С1 т.е. максимальное количество информации, которое способен передавать канал в ту же единицу времени. Возникает вопрос: какова должка быть пропускная способность канала, чтобы он «справлялся» со своей задачей, т.е. чтобы информация от источника X к приемнику Y поступала без задержки? Ответ на этот вопрос дает первая или прямая теорема Шеннона.
Если пропускная способность канала связи C1 больше энтропии источника информации в единицу времени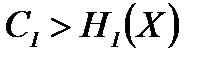 
, то всегда можно закодировать достаточно длинное сообщение так, чтобы оно передавалось каналом связи без задержки. Если же, напротив, 
, то передача информации без задержек невозможна.
С помощью расчетов может быть определена пропускная способность канала, когда число элементарных символов более двух и когда искажения отдельных символов зависимы. Зная пропускную способность канала, можно определить верхний предел скорости передачи информации по каналу с помехами.
2-я (обратная) теорема Шеннона.
Пусть имеется источник информации X, энтропия которого в единицу времени равна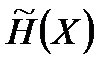 
и канал с пропускной способностью С. Тогда если 
, то при любом кодировании передача сообщений без задержек и искажений не возможна. Если же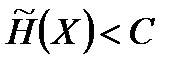 
, то всегда можно достаточно длинное сообщение закодировать так, чтобы оно было передано без задержек и искажений с вероятностью, сколь угодно близкой к единице.
Понятие линейных кодов.
Предположим, что число символов на входе канала q является некоторой степенью простого числа р. Входные символы канала представляют собой обозначения для реальных сигналов в канале; для удобства обращения с ними возьмем в качестве входного алфавита 
канала конечное поле 
из q элементов. Введено предположение о том, что q является степенью простого числа. Число элементов в любом конечном поле есть степень простого числа и, наоборот, для любого q, являющегося степенью простого числа, существует поле из q- элементов.
Пусть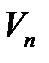 
- векторное пространство размерности n над полем . Подпространства размерности k пространства 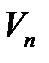называются q-ичными линейными кодами длины n с k информационными символами (или 
- кодами). Если С - линейный код, то подпространства линейного пространства С будем называть (линейными) подкодами кода С.
Вес Хемминга вектора v из 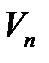число ненулевых компонент этого вектора w(v). Расстояние Хемминга 
между векторами 
определим как вес их разности, а именно положим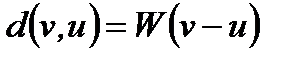 
. Пусть 
минимальное расстояние линейного кода С.
Задания линейного кода матрицей G: Пусть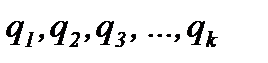 
- некоторый базис (n, k) - кода С, и пусть G - матрица из k строк и n столбцов, i-й строкой которой является базисный вектор qi. Матрица G называется порождающей матрицей кода С. Поскольку каждый из k коэффициентов линейной комбинации может принимать q значений, общее число кодовых векторов в коде С равно qk.
Для задания линейных кодов используются также матрицы Н: Пусть CД — множество всех векторов 
, такие, что для любого 
. 
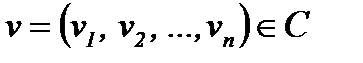(13.2)
Пусть проверочная матрица линейного (n, k) -кода С имеет вид 
. Тогда матрица 
является порождающей матрицей кода С. Справедливо и обратное.
Минимальный вес линейного (n, k) - кода С равен d тогда и только тогда, когда любые (d-1) столбцов проверочной матрицы этого кода линейно независим, но некоторые d столбцов проверочной матрицы линейно зависимы.
Векторное пространство 
- множество n - последовательностей элементов из 
с покомпонентным сложением и умножением на скаляр. Линейный код есть подпространство в .
Каждое слово в линейном коде связано с остальными словами кода так же, как любое другое кодовое слово. Расположение соседних кодовых слов вокруг нулевого слова есть типичное расположение слов вокруг любого другого кодового слова. Для определения минимального расстояния линейного кода достаточно определить расстояние между нулевым словом и ближайшим к нему кодовым словом.
Для линейного кода минимальное расстояние d* находится из равенства 
(13.3), где минимум берется по всем кодовым словам, кроме нулевого.