Цилиндрические зубчатые передачи

Глава 3. Основы проектирования деталей машин

Основные понятия

Деталь – изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций.

Сборочная единица – изделие, составные части которого подлежат соединению между собой сборочными операциями на предприятии-изготовителе.

Механизм – совокупность сборочных единиц и деталей, которые находятся в определённой взаимосвязи и обеспечивают необходимое функционирование.

Привод – устройство для приведения в действие машин и механизмов. Он состоит из двигателя, передаточного механизма и системы управления.

Машина – система, осуществляющая механическое движение, необходимое для выполнения рабочего процесса.

Машины делятся на транспортные, энергетические, технологические и др.

Классификация деталей машин

Соединения предназначены для фиксации взаимного положения деталей и объединения их в сборочные единицы и узлы, например, сварные, заклёпочные.

Передачи осуществляют передачу энергии от двигателя к исполнительному органу:

– передачи зацеплением (цилиндрические, конические, червячные, цепные), трением (ременные, фрикционные);

– элементы, преобразующие движение (рычажные, кулачковые).

Несущие и базирующие элементы:

– валы и оси;

– подшипники;

– направляющие, поддерживающие поступательно движущиеся детали;

– корпусные и несущие детали – основные части редуктора, воспринимающие нагрузки.

Особые группы:

– устройства для защиты от загрязнений и смазывания (уплотнения, кожухи, крышки);

– упругие элементы (пружины, рессоры, амортизаторы).

Требования к деталям машин

Работоспособность – способность изделия выполнять заданные функции с параметрами, установленными в техническом задании.

Техническое обслуживание – этап эксплуатации, направленный на поддержание надёжности и готовности технических объектов и их элементов.

Надёжность – свойство изделия выполнять в течение заданного времени или заданной наработки свои функции, сохраняя в заданных пределах эксплуатационные показатели.

Долговечность – свойство изделия, позволяющее ему сохранять работоспособность до предельного состояния с необходимыми перерывами для технического обслуживания и ремонта.

Ремонт – совокупность технических мероприятий, осуществляемых с целью восстановления работоспособности устройства.

Механические передачи

Механической передачей называется механизм, передающий энергию от двигателя к исполнительному органу машины с преобразованием скоростей, сил и моментов, а иногда характера и закона движения.

Редуктор – передаточный механизм, служащий для понижения частоты вращения, увеличения вращающего момента. Мультиприкатор – механизм, повышающий частоту вращения.

На рис. 3.1 показаны редукторы:

а – одноступенчатый с цилиндрическими зубчатыми колесами;

а)

Рис.3.1

д)

г)

в)

б)

б – одноступенчатый с коническими зубчатыми колесами;

в– червячный;

г – двухступенчатый коническо-цилиндрический;

д – двухступенчатый соосной схемы (оси валов I и III совпадают).

Двухступенчатые редукторы обеспечивают получение больших передаточных отношений i, от 6,3 до 64.

Корпуса редукторов обычно делают составными из двух частей с осевой или радиальной сборной. При осевой сборке разъем корпуса выполняют перпендикулярно осям валов (рис. 3.2а), а при радиальной – по плоскости, проходящей через оси валов (рис. 3.2б).

 

а)

б)

Рис.3.2

О

О

Разъем

К

К

На рис. 3.3 показан двухступенчатый редуктор с радиальной сборкой и цилиндрическими колёсами, типичный для общего машиностроения. Корпус состоит из основания 5 и крышки 4. Они соединены болтами 6 и штифтами 9. Крышка 3 с отдушиной 2 служит для осмотра и заливки масла, пробка 8 для слива масла, маслоуказатель 7 для определения уровня масла, рем-болты 1 для переноса подъемным краном. Внутри корпуса располагаются тихоходный вал 11 с зубчатым колесом 10, промежуточный вал 14 с нарезанными зубьями и насаженным зубчатым колесом, быстроходный вал с нарезанными зубьями 15 и подшипники.

На рис.3.4 представлен внешний вид редукторов:

а – цилиндрического двухступенчатого; б – одноступенчатого косозубого; одноступенчатого конического.

По способу передачи движения от ведущего звена к ведомому различают передачи трением и зацеплением. Передачи зацеплением с непосредственным контактом: зубчатые, червячные, цепные.

 

Рис.3.3

Уровень масла

Рис.3.4

б)

а)

в)

 

На рис. 3.5 показаны передачи:

а – цилиндрическая прямозубая передача с параллельными осями и внешним зацеплением;

 

а)

Рис. 3.5

б)

в)

г)

д)

е)

Рис. 3.5

б – цилиндрическая прямозубая передача с внутренним зацеплением;

в – косозубая цилиндрическая передача с внешним зацеплением;

г – прямозубая коническая передача с пересекающимися осями;

д – косозубая коническая передача;

е – червячная передача.

Цилиндрические зубчатые передачи

Это передачи с параллельными осями. Они бывают с прямым, косым зубом и шевронные. Передачи с шевронным и косым зубом имеют преимущества: большая прочность зуба, большая плавность зацепления и малый шум, меньшие динамические нагрузки.

На рис. 3.6 показана передача с наружным зацеплением, где n ₁, n ₂ – частоты вращения шестерни 1 и колеса 2, z ₁ и z ₂ – числа их зубьев, d ₁ и d ₂ – диаметры делительных окружностей.

Отношение частот вращения называется передаточным отношением i ₁₂. В отличие от передаточного числа u ₁₂ оно имеет знак.

Из очевидных равенств скоростей точек колеса и шестерни, расположенных на делительных окружностях

,

получаем передаточное отношение

,

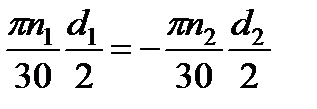Чаще всего используют зубчатые колёса с эвольвентным зацеплением, которое обеспечивает постоянное передаточное отношение и малое скольжение зубьев. Рабочая поверхность зуба имеет форму эвольвенты. Эвольвентой называется кривая, которую описывает точка N ₁, образующей прямой N - N при перекатывании без скольжения по окружности (рис. 3.7). Окружность, по которой перекатывается образующая кривая N - N называется основной. Радиус кривизны эвольвенты переменный. При увеличении радиуса основной окружности до бесконечности радиус кривизны эвольвенты в любой ее точке также становится бесконечно большим, т.е. основная окружность и эвольвента превращаются в прямые линии. Эвольвентное зубчатое колесо превращается в зубчатую рейку с прямолинейным профилем зуба.

Рис.3.7

Рис.3.6

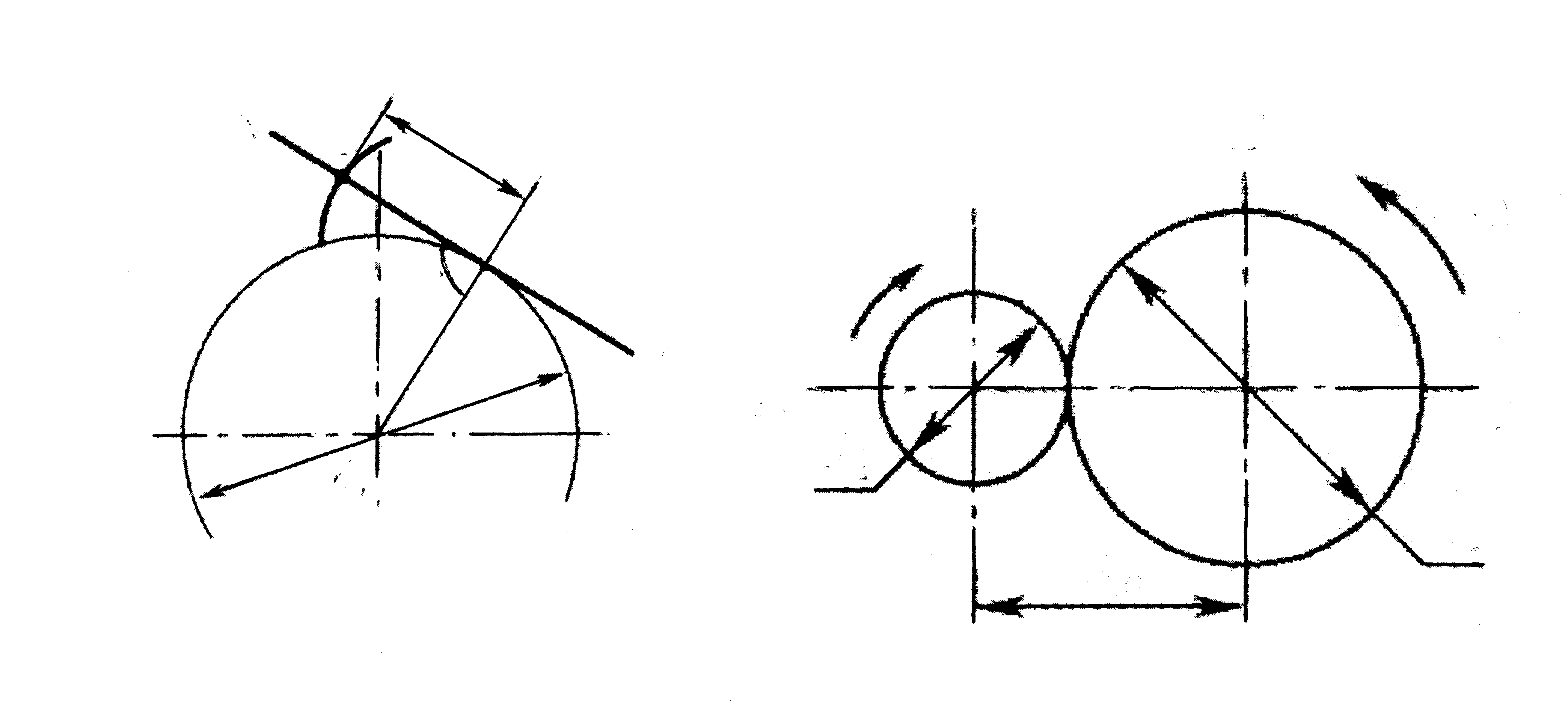
n 1

aw

n 2

d 1

z 1

d 2

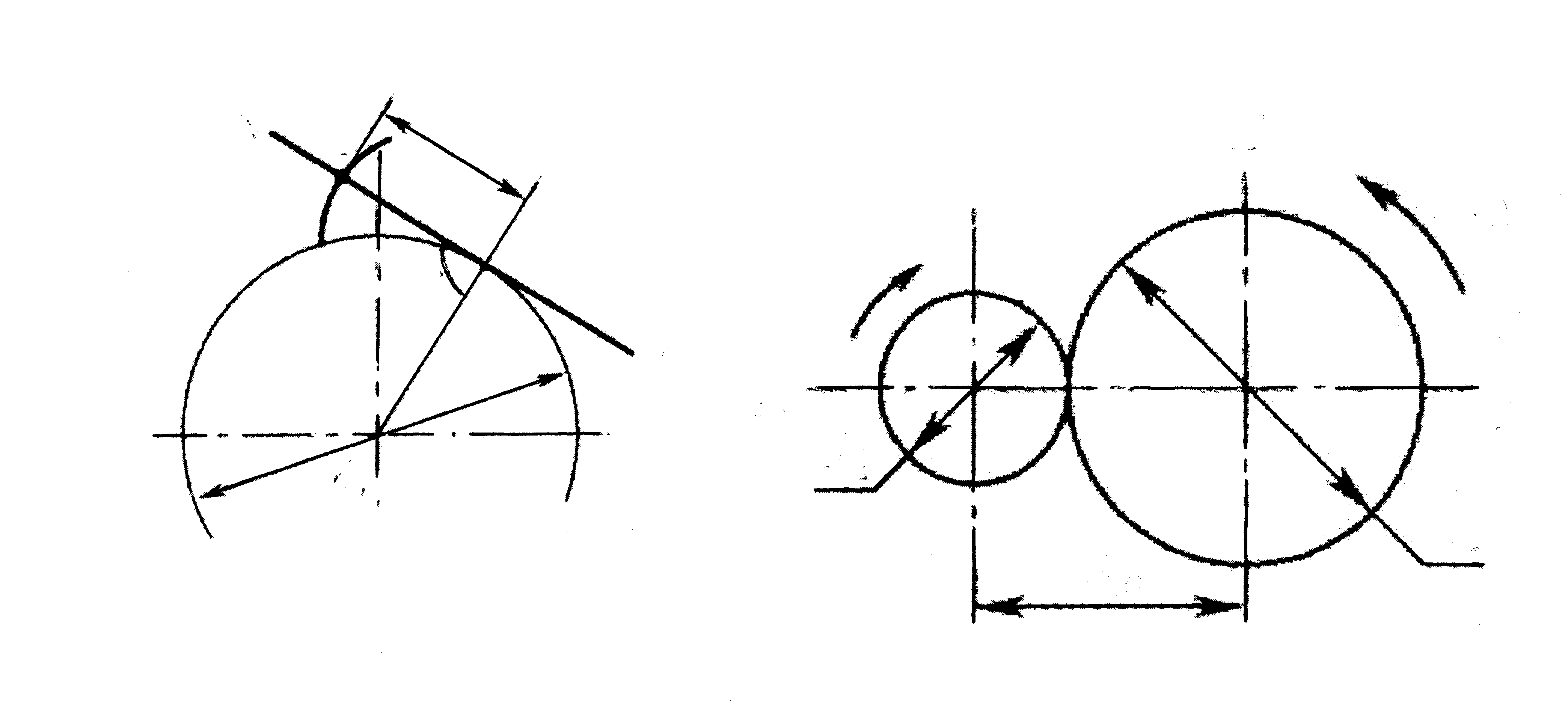
N

N

N 1

90°

ρ

db

Прямозубое колесо нарезается с помощью долбяка или инструментальной рейки (рис.3.8а,б). Долбяк совершает возвратно-поступательное движение вдоль оси заготовки и вращается вместе с ней. При нарезании зуборезной гребенкой заготовка вращается вокруг своей оси, а рейка 1 совершает возвратно-поступательное движение параллельно оси заготовки 2 и поступательное движение по касательной к ободу заготовки.

Окружность зубчатого колеса, на которой шаг p и угол зацепления равны углу и шагу профиля α инструментальной рейки называется делительной. Её диаметр обозначают d. На рейке делительной плоскостью называют такую, на которой толщина зуба равна ширине впадины (рис.3.9).

+x

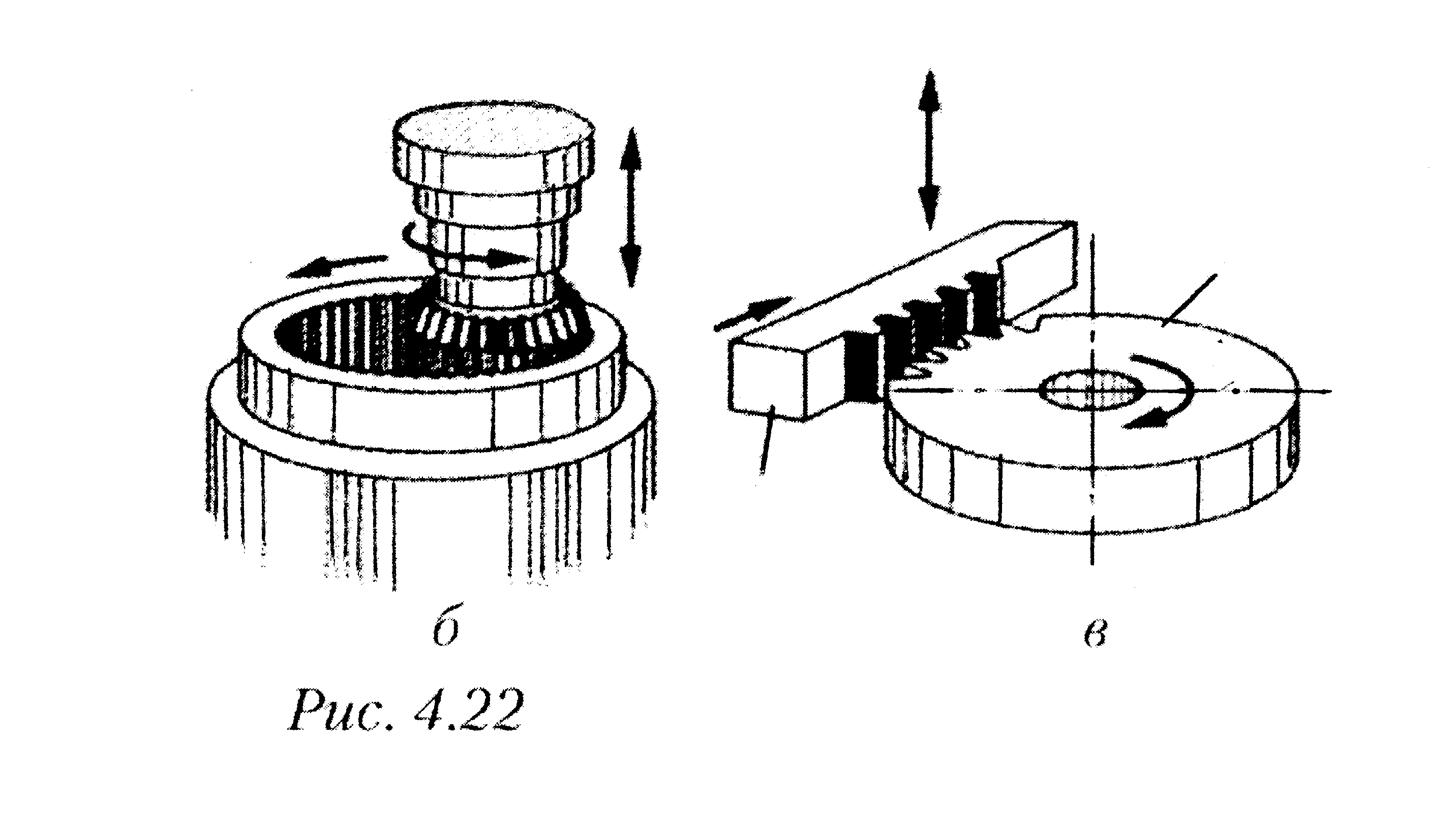
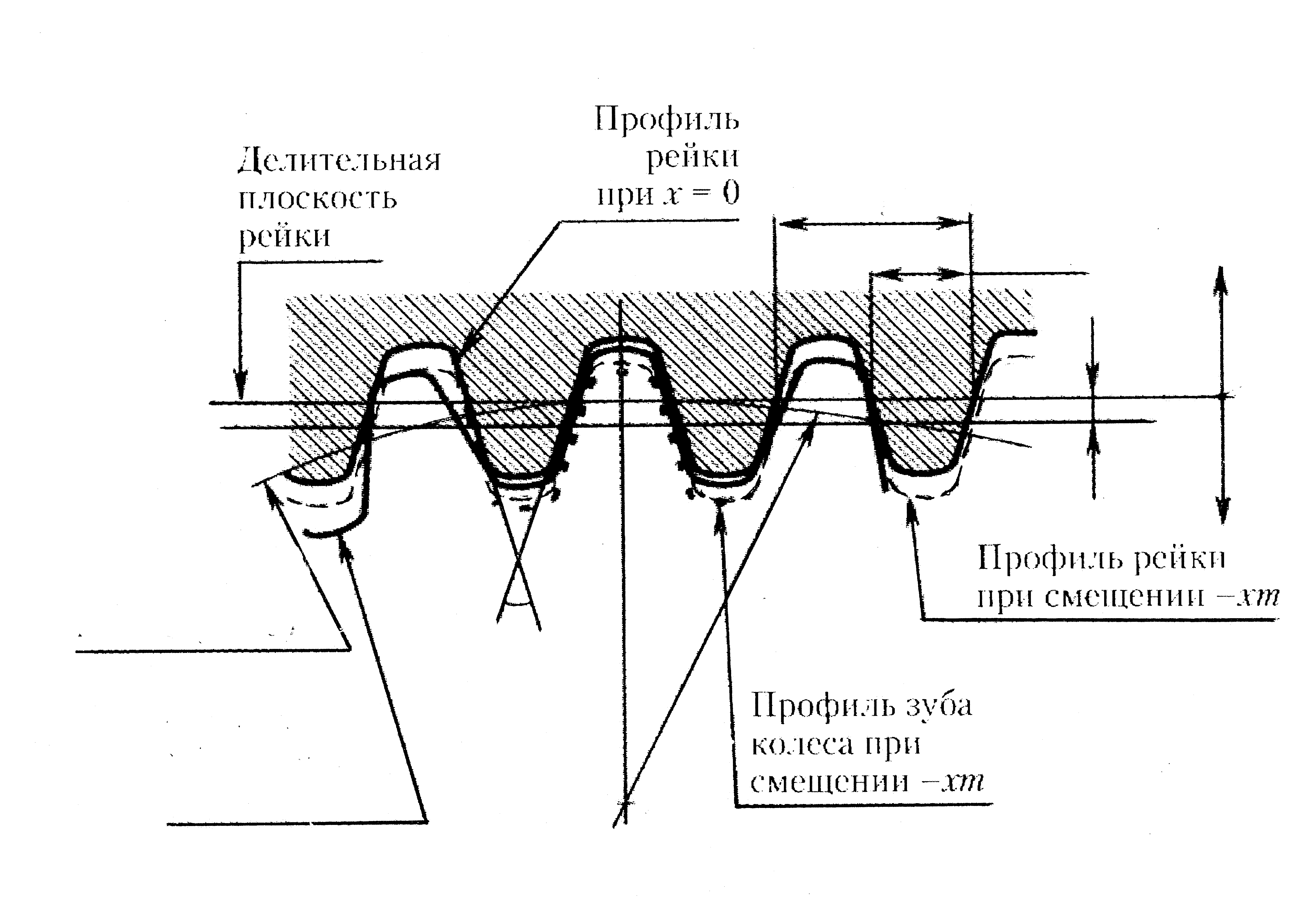
Рис.3.9

Рис.3.8

б)

а)

Делительная окружность колеса

Профиль зуба колеса (х = 0)

Профиль зуба колеса (- xm)

Профиль рейки при смещении х = 0

Делительная плоскость рейки

Профиль рейки (- xm)

pt

0,5 pt

- x

- xm

d

2 α

O

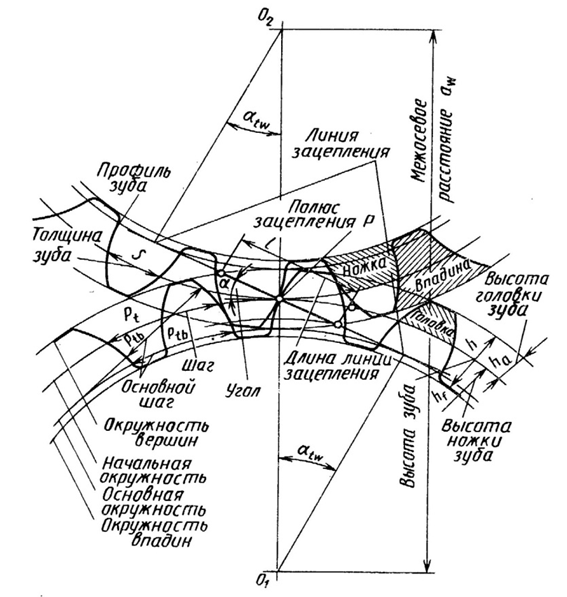
При вращении зубчатых колёс зуб колеса 2 входит в контакт с вершиной зуба колеса 1 в точке В (рис.3.10а). При дальнейшем вращении контакт смещается к его вершине от впадины. Геометрическое место точек контакта профилей, которое они занимают в процессе работы пары зубьев, называется линией зацепления. Эвольвентные профили зубьев в точке контакта имеют общую нормаль, представляющую собой прямую касательную к основным окружностям колёс, независимо от расположения контакта. Поэтому линия зацепления N - N является прямой. Эта линия определяет начало входа пары зубьев в зацепление и выхода из него. Отрезок АВ, ограниченный окружностями вершин зубьев колеса и шестерни, называется активным участком линии зацепления. Нормальные силы в контакте двух зубьев направлены по нормалям к их профилям, то есть вдоль линии зацепления. Это обеспечивает постоянство передаточного отношения по вращающему моменту.

Линия, соединяющая центры зубчатых колес называется межосевой. Точка пересечения линии зацепления и межосевой называется полюсом зацепления. Окружности, перекатывающиеся одна по другой без скольжения, называются начальными. Их диаметры обозначаются d_{ω 1}и d_{ω 2}. Полюс может быть определен как точка касания начальных окружностей. Угол α, образованный перпендикуляром к межосевой линии с линией зацепления называется углом зацепления.

Окружной делительный шаг p – это расстояние между одноименными профилями соседних зубьев, измеряемое по дуге делительной окружности. Основным параметром зубчатого зацепления является модуль, представляющий собой отношение делительного шага к числу π

 

Рис.3.10

M 1

a)

б)

dw 1

O1

A

O2

M 2

dw 2

da 1

da 1

df 1

df 2

α

α

αw

ρ 1

ρ 2

z 1

z 2

N

N

P

B

90°

90°

bw

aw

ГОСТ предусматривает угол зацепления α = 20°, высоту головки зуба h_a = m, высоту ножки зуба h_f = 1,25 m (рис.3.10б).

Диаметры делительных окружностей колес определяются через модуль зацепления зависимостями

где z ₁, z ₂ – число зубьев первого и второго колеса.

Силы в зацеплении цилиндрических передач

Рассмотрим цилиндрическую передачу с косым зубом. Угол наклона зуба к осевой линии зубчатого колеса β составляет 8...20^° (рис.3.11). Сверху показано сечение зуба нормальной плоскостью n - n. В контакте зубьев возникает нормальная сила направленная вдоль нормали к поверхностям зубьев, составляющей угол α_n – угол зацепления в нормальном сечении. Начало координат выберем в полюсе зацепления на середине зубчатого венца.

Сила взаимодействия раскладывается на три составляющие

где F_t = 2 M/d – окружная сила;

M – вращающий момент;

– радиальная сила;

α_t – угол зацепления в торцевом сечении;

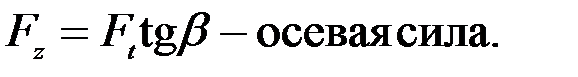
Нормальная к поверхности зуба сила равна

В расчётах зубьев на прочность учитывают динамические нагрузки путём умножения номинальных момента и силы на коэффициент динамичности k _дин

, ,

где k _дин принимают равным 1,05...2.

β

n

Fn

αn

Fz

Ft

Fxz

Fn

Fy

Fy

Ft

Fz

Fxz

n

β

αt

βb

αn

z

x

а)

Рис.3.11

б)

Удельную нагрузку на зуб получают делением окружной силы на ширину зуба b_w (рис.3.10).

Удельная нагрузка в расчётах на контактную выносливость определяется с учетом ряда коэффициентов

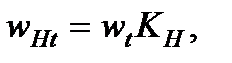
где

– коэффициент, учитывающий распределение нагрузки между зубьями;

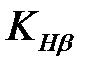– коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;

– коэффициент, учитывающий дополнительную динамическую нагрузку.

При расчете на выносливость при изгибе удельная нагрузка определяется с учетом аналогичных коэффициентов.

Расчёт зубьев на прочность

Расчет по контактным напряжениям

Переменные контактные напряжения являются причиной усталостного разрушения рабочей поверхности зубьев. Они приводят к появлению в поверхностном слое трещин и выкрашиванию частиц материала.

Максимальные контактные давления определяются по формуле Герца

где 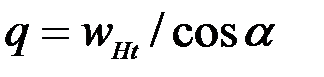– удельная нагрузка;

– удельная окружная сила;

– приведенный модуль упругости;

Е ₁, Е ₂ –модули упругости материалов колес;

– приведенный радиус кривизны поверхностей зубьев, знак + берётся для выпуклых поверхностей.

Контактные напряжения не одинаковы по высоте зуба. В связи с тем, что выкрашивание наблюдается у делительной окружности, максимальное напряжение определяют для положения, когда начальная точка контакта зубьев находится в полюсе зацепления.

Если контакт зубьев располагается в полюсе P, радиусы кривизны профилей зубьев равны (рис.3.10)

Учитывая это, а также выражение для q, для максимальных контактных напряжений, получаем

,

где u – передаточное число,

знак «+» берется при внешнем зацеплении;

– коэффициент, учитывающий форму поверхностей зубьев в полюсе, при α = 20^°, Z_H = 2,5;

– коэффициент, учитывающий механические свойства материалов колёс, для стальных колёс

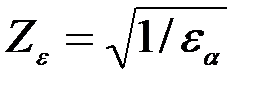– коэффициент, учитывающий суммарную длину контактных линий с учётом перекрытия.

Коэффициент торцевого перекрытия 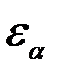определяет плавность работы передачи. Он равен отношению угла поворота колеса от входа торцового профиля зуба в зацепление до выхода к угловому шагу 2 π / z, или отношению длины активного участка линии зацепления к окружному шагу. Для прямозубых передач он должен быть 1,25..1,9.

Приближённая формула для его определения

В расчётах на выносливость используется кривая контактной выносливости. Если задан ресурс работы зубчатой передачи T_h, то число циклов изменения контактных напряжений равно

N_HЕ = 60 сnT_h,

где с – число контактов одной поверхности зуба за один оборот;

n – частота вращения.

σH lim i

σH lim

NH

NHE

Рис.3.12

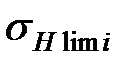По кривой контактной выносливости определяется напряжение , при котором зуб выдерживает N_НЕ циклов нагружения (рис.3.12).

Допускаемые контактные напряжения равны

,

где S_H = 1,2...1,35 – запас прочности.

Условие контактной прочности

Межосевое расстояние для стальных колёс определяют по формуле

где М ₁ – расчётный вращающий момент на шестерне в H·мм;

коэффициент K_H учитывает неравномерность распределения нагрузки по ширине зуба;

– относительная ширина зуба, принимается равной 0,1…0,3.

Модуль связан с межосевым расстоянием зависимостью

Расчет зуба на прочность при изгибе

Рис.3.13

опасное

сечение

Ft

F

Fr

d

df

σ

σсж

σи

s

h 1

α

F

Расчет проводится для наиболее неблагоприятного варианта приложения силы к вершине зуба, которая передается одной парой зубьев (рис.3.13). Силу F по линии действия переносят к оси симметрии зуба и раскладывают на составляющие

F_t = 2 M ₁/ d ₁, F_r = F_t tg α.

После введения коэффициента K_F, учитывающего распределение нагрузки между зубьями, неравномерность его по ширине зуба и динамическую добавку, внутренние усилия в опасном сечении зуба равны

M _из = F_tK_Fh ₁,

N = F_r = F_tK_F tg α.

Растягивающие напряжения в опасной точке сечения

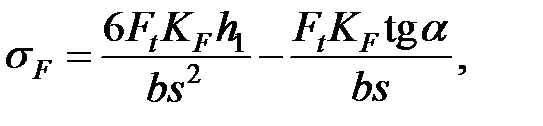
где – момент сопротивления;

A = bs – площадь сечения;

s – толщина зуба у основания.

После умножения и деления на m получаем

где – коэффициент формы зуба.

Для внешнего зацепления

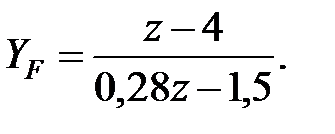
Если задан ресурс T_h, число циклов нагружения зуба равно

N_NE = 60 cnT_h.

С использованием кривой выносливости по значению
N_NE определяется предел ограниченной выносливости зубьев при изгибе для отлулевого цикла σ_{F lim}.

Допускаемое напряжение в опасном сечении зуба равно

,

где S_F = 1,55…1,75 – коэффициент запаса прочности при изгибе.