Конические зубчатые передачи

Конические зубчатые передачи используются для передачи вращения между пересекающимися осями. Назначение – изменять межосевой угол расположения валов, что может сочетаться с изменением угловых скоростей и моментов.

Обычно межосевой угол равен 90^º.

Геометрия конической передачи

Рис.3.14

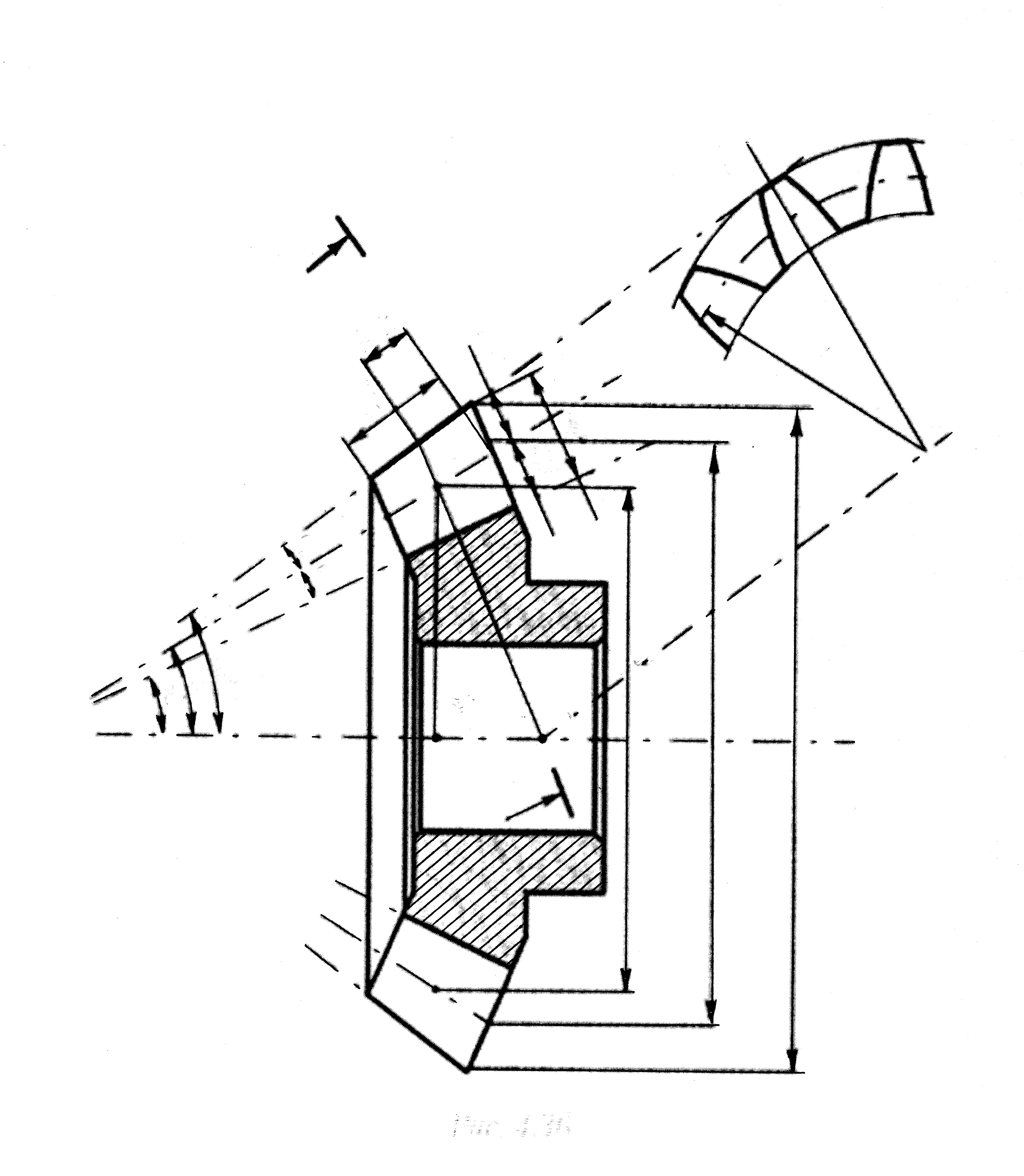
А - А

А

А

δа

δ

δf

θ

θ

b/ 2

b

b

P

O 1

O 2

hae

he

hfe

dm

de

dae

dv

В отличие от делительных цилиндров в цилиндрических передачах здесь делительные конусы с углами δ, углы конусов вершин и впадин зубьев δ_a и δ_f. Следующие параметры задаются для внешнего торца конических колёс, где их легко измерить:

внешний диаметр делительной окружности

d_e = m_tez,

средний диаметр делительной окружности

d_m = d_e (1-0,5 ψ_bR)

где ψ_bR = b / R_e,

b – ширина зубчатого венца;

R_e – внешнее конусное расстояние (длина образующей конуса от вершины до внешнего торца);

высоты головки, ножки и полная высота зуба

h_ae = m_te; h_fe = 1,2 m_te; h_e = 2,2 m_te.

Вершины делительного и внутреннего конусов совпадают. Зубья понижаются и сужаются от торца к центру.

На рис. 3.15 показана ступень редуктора с конической передачей. Коническая шестерня 2 установлена консольно на валу 4, а колесо 6 на валу 5, закрепленном на двух опорах (конических подшипниках). Конические подшипники необходимы для восприятия осевых

Рис.3.15

сил, возникающих в конической передаче.

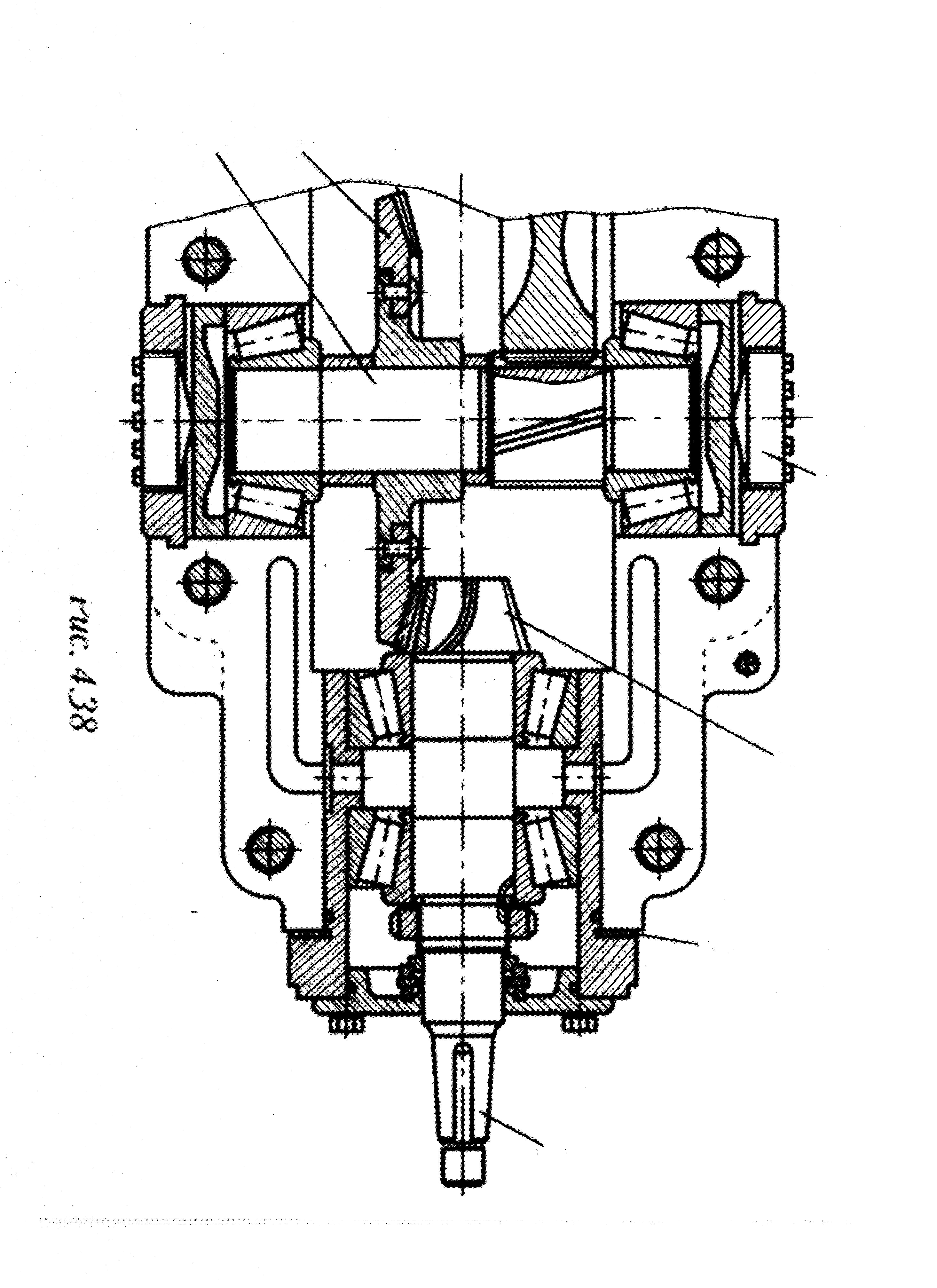
Коническая передача требует точной фиксации колес вдоль осей для обеспечения совпадения вершин конусов. Вал 4 в сборе с подшипниковыми узлами может смещаться за счет шайбы 3, а вал 5 с помощью двух винтов 1.

Червячные передачи

Оси валов червячной передачи обычно перекрещиваются под углом 90^º. Она состоит из червяка с числом витков z ₁и червячного колеса с числом зубьев z ₂. Червячные передачи позволяют получить большие передаточные отношения

.

Число заходов червяка равно z ₁ = 1, 2 или 4. В зависимости от формы профиля витков различают архимедовы, конволютные и эвольвентные червяки.

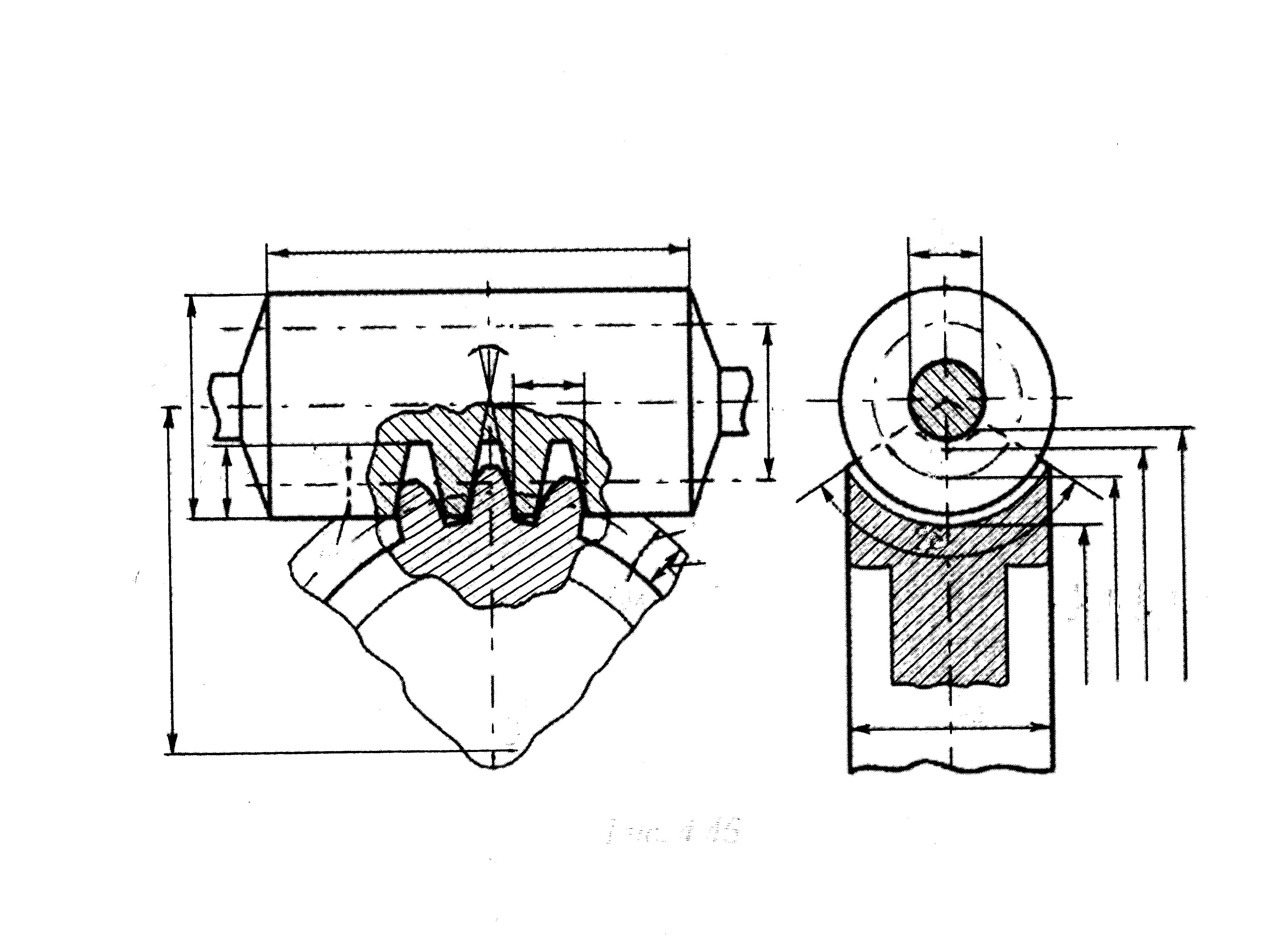
Схема червячной передачи показана на рис 3.16. Червяк характеризуется следующими параметрами (архимедов червяк)

угол профиля α = 20º;

высота зуба h = 2,2 m, головок витка червяка и зуба червячного колеса h_a1 = h_a2 = m, высота ножек h_f1 = h_f2 = 1,2 m;

Рис.3.16

aw

da 1

b 1

hf 1

ha 2

h 1

h 2

ha 1

hf 2

2 α

p

O

d 1

df 1

b

2 δ

b 2

df 2

da 2

daw2

d 2

делительный диаметр червяка d ₁ = mq, где q = 8…20 – коэффициент диаметра червяка, q должен быть не менее 0,25 z ₂.

 

Геометрические параметры червячного колеса задаются для среднего сечения

делительный диаметр d ₂ = mz₂;

угол обхвата колеса 2 δ = 90…120º;

ширина колеса b ₂ = (0,67…0,75) d_{a 1},

где d_{a 1} – диаметр вершин червяка;

длина червяка b ₁ ≤ (11+0,06 z ₁) m при z ₁ = 1 и 2; b ₁≥ (12,5+0,09 z ₁) m при z ₁ = 4;

угол подъема витка червяка γ.

Межосевое расстояние червячной передачи равно

.

Червячная передача обладает свойством самоторможения или необратимости движения.

Коэффициент полезного действия червячной передачи приближенно равен

где – приведенный угол трения.

Для стального червяка и бронзового колеса

скорость скольжения v_s, м/с φ ^'

0,01 6^º30'

1,0 2^º40'

10,0 1^º

При малом γ и z ₁ = 1, ɳ ˂0,5.

Силы в червячном зацеплении

Силу взаимодействия между червяком и червячным колесом можно разложить на три составляющие: окружная сила на колесе F_{t 2} равна осевой силе на червяке F_{а 1} = 2 M ₂/ d ₂, окружная сила на червяке F_{t 1} равная осевой силе на колесе F_{а 2} = 2 M ₁/ d ₁, радиальная сила

F_{r 1} = F_{r 2} = F_{t 2}tg α,

где M ₁, M ₂ – вращающие моменты на червяке и колесе.

Расчет зубьев стальных червяков не проводят. Зубья бронзовых колес рассчитывают на контактную прочность, а расчет на изгиб выполняют как проверочный. Для определения максимальных давлений в контакте зубьев колеса и червяка используется зависимость

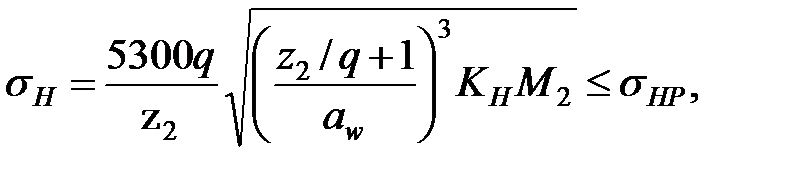
где М ₂ – вращающий момент на червячном колесе, Н∙м.

Червячные редукторы

Редуктор может иметь компоновку с нижним и верхним, горизонтальным и вертикальным расположением червяка. При больших размерах колеса его делают составным из стального центра и обода с зубчатым венцом из бронзы. На рис. 3.18 показан червячный редуктор с радиальной сборкой и горизонтальным расположением червяка, где 1 – червяк, 2 – составное червячное колесо. Для осевой регулировки колеса для обеспечения хорошего контакта витка червяка с зубом колеса установлены кольца K.

Ременные передачи

Ременная передача состоит из ведущего и ведомого шкивов, соединенных ремнем, надетым на шкивы с натяжением (рис.3.19а). Вращение ведущего шкива передается к ведомому благодаря трению, имеющему место между шкивами и приводным ремнем. Передача дает возможность передавать вращение между валами, расположенными на значительном расстоянии, характеризуется плавностью и бесшумностью работы, высоким коэффициентом полезного действия до 0,96.

По типу ремней передачи различаются

– с плоскими ремнями (рис. 3.19б);

– с клиновыми нормального сечения, узкими и широкими, поликлиновыми (рис.3.19в);

– с зубчатыми ремнями (рис. 3.19г).

Зубчатые ремни устанавливают без предварительного натяжения. Они работают бесшумно и обеспечивают постоянное передаточное отношение.

Ремни изготавливают из прорезиненных тканей, с высокопрочным шнуровым кордом, кожаные.

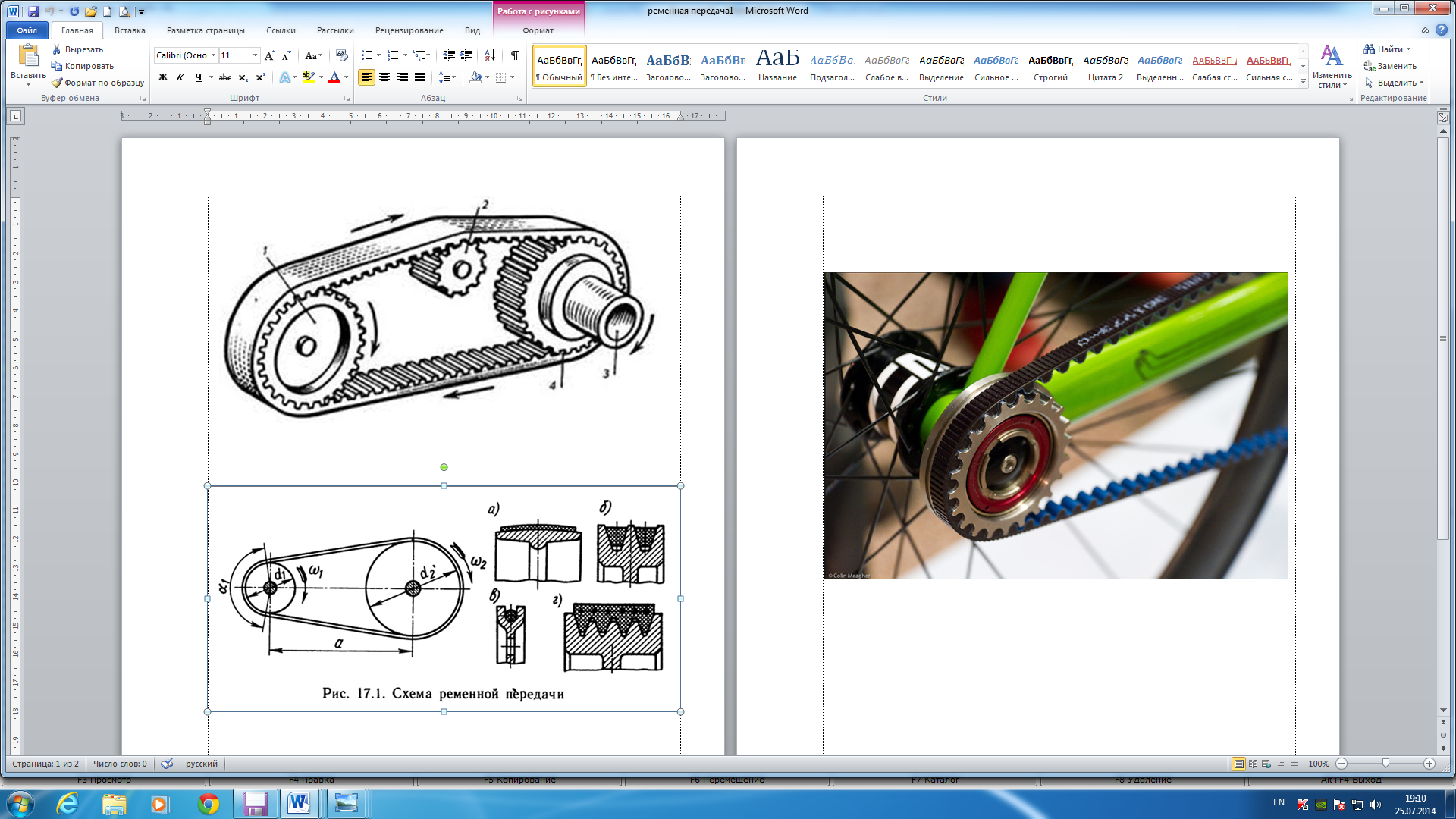
Рис.3.19

д)

г)

в)

б)

а)

α 2

β 2

β 1

α 1

F 2

O 2

O 1

F 1

Шкивы изготавливают из чугуна, стали, легких сплавов, пластмасс, дерева.

Кинематика, геометрия и силы в ременных передачах

Параметры передачи: α ₁, α ₂ – углы обхвата шкива ремнем; a – межосевое расстояние; β ₁, β ₂ – дуги, на которых наблюдается скольжение.

На рис. 3.19д показаны ведущий шкив 4 и ведомый 2. При работе передачи в ведущей ветви ремня 3 возникает большая сила F ₁,чем F ₂ в ведомой ветви. Вследствие этого деформация ремня на подходе к шкиву 4 больше, чем на сходе. Изменение деформации происходит за счет проскальзывания ремня на дуге β ₁. Поэтому в ременных передачах наблюдается упругое скольжение ремня относительно шкивов.

Окружные скорости шкивов равны

; ,

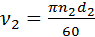где n ₁, n ₂ – частоты вращения шкивов.

Они связаны между собой соотношением

,

где = 0,01…0,02 – коэффициент упругого скольжения.

Передаточное отношение i = n ₁/ n 2 выбирают равным не более 4-5 (i = d ₂/ d ₁(1- )).

Геометрия передачи

Диаметр меньшего шкива плоскоременной передачи принимают равным

,

где P ₁ – мощность, кВт.

Угол обхвата ремнем меньшего шкива

Рекомендуется принимать для плоскоременной передачи и для клиноременной.

Длина ремней передачи равна

.

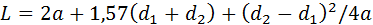Она принимается равной стандартной.

Силы

Окружная сила равна разности натяжений ветвей ремня

F_t = F ₁- F ₂.

Предварительное натяжение ремня равно

,

где A – площадь поперечного сечения ремня;

– напряжение при предварительном натяжении ремня, принимаемое 2 МПа для плоских, 1,2...1,5 МПа для клиновых ремней.

Силы натяжения ветвей ремня при работе передачи без учета центробежных сил равны

, ,

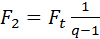где q = e^fβ – величина, определяемая из решения Эйлера для нити, скользящей по цилиндру;

β – угол скольжения, принимается равным 0,7 угла обхвата α.

Напряжение в ремне

В поперечных сечениях ветвей ремня возникают нормальные напряжения:

– связанные с усилиями натяжения

;

– от изгиба ремня на дуге обхвата

где E = 200…600 МПа – модуль упругости;

δ – толщина ремня;

– от центробежной силы

,

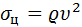где – плотность материала ремня;

υ – линейная скорость ремня.

Максимальное напряжение возникает в ведущей ветви ремня. Оно равно сумме трех составляющих.

Допускаемое напряжение принимается равным

,

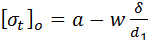где a = 2…3 МПа, w = 10…17 МПа.

Цепные передачи

Цепная передача состоит из ведущей 2 и ведомой 1 звездочек, огибаемых цепью (рис.3.20). Их преимущество перед ременными: могут передавать движение при значительных межосевых расстояниях между валами, могут передавать большие мощности, силы предварительного натяжения малы.

Недостатки: значительный шум, быстрое изнашивание шарниров цепи.

Приводные цепи

Основные типы: роликовые, втулочные и зубчатые.

Роликовая цепь состоит из внутренних 1 и наружных 2 пластин (рис.3.21). В наружные пластины запрессованы валики 5, пропущенные через втулки 4. На втулки напрессованы внутренние пластины. На втулки свободно одеты ролики 3. Зацепление цепи со звездочкой происходит через ролик, который перекатывается по зубу и уменьшает его износ.

Втулочные цепи отличаются от роликовых тем, что не имеют роликов.

Одной из важных характеристик цепи является её длина, которая может быть вычислена с использованием зависимости для определения потребного числа звеньев

где a – расстояние между осями звездочек;

z ₁, z ₂– число зубьев ведущей и ведомой звездочек;

p – шаг цепи.

в)

Рис.3.20

Рис.3.21

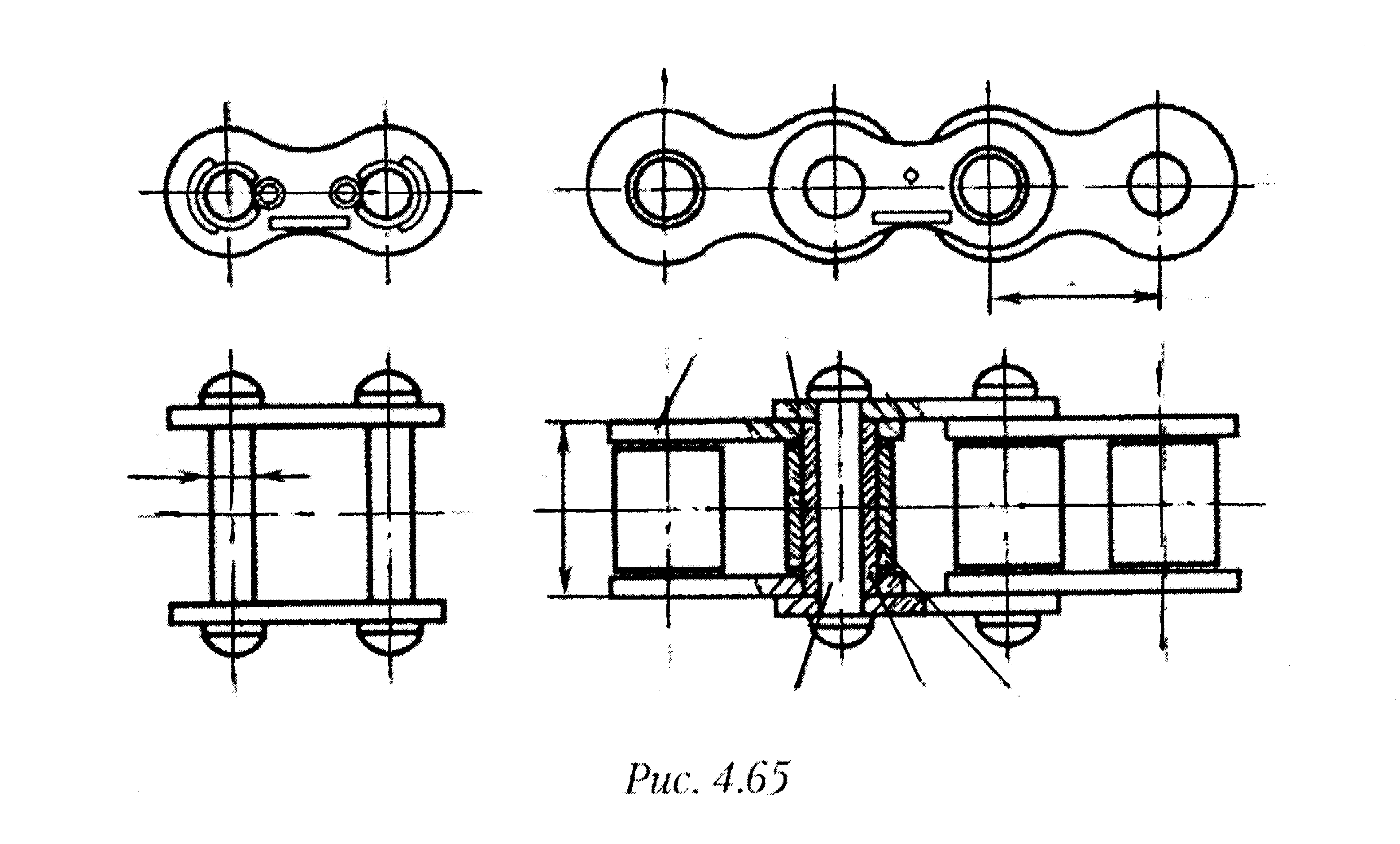
d 0

b

p

Сила натяжения ведущей ветви цепи равна сумме составляющих:

- окружной силы F_t = 2 M / d,

где d - делительный диаметр звездочки;

- предварительного натяжения цепи F ₀= k_fqag,

где k_f -коэффициент провисания, зависящий от угла наклона линии центров звездочек к горизонту;

q – масса одного метра цепи;

- центробежной силы F_v = qv ²,

где v - скорость цепи.

Работоспособность цепных передач определяется изнашиванием шарниров, поэтому основным является расчет, направленный на обеспечение износостойкости шарниров.

Для втулочной цепи нагрузочная способность определяется из условия, чтобы среднее давление в шарнире звена р_ц не превышало допускаемого [ р_ц ] = 15…35 МПа

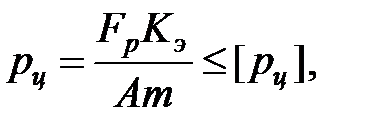
где F_p – расчетная сила натяжения цепи;

K _э= 0,64…1,25 – коэффициент, учитывающий способ смазывания, угол наклона линии центров звездочек, способ регулировки натяжения цепи;

A = d ₀ b – площадь проекции опорной поверхности шарнира на осевую плоскость,

d ₀– диаметр втулки;

b – длина втулки;

m – коэффициент рядности цепи.