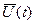Сравнение эффективности работы разомкнутых и замкнутых

УТВЕРЖДАЮ

и.о. Зав. кафедрой ПИ

______________/В.А. Макаров/

«___»__________20__

 

КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

Тееория автоматического управления
(наименование дисциплины)
Направление подготовки	15.04.04 Автоматизация технологических процессов и производств
	(код и наименование)
Профиль	Разработка промышленных автоматизированных систем
	(код и наименование)
Форма обучения	очная
	(очная, очно-заочная, заочная)
Программа подготовки	Академическая магистратура
	(академический, прикладной бакалавриат)
Квалификация выпускника

 

Москва 2018

 

Оглавление

Лекция 1

1.Введение 3

1.1 Задачи анализа и синтеза 7

1.2.Сравнение эффективности работы разомкнутых и замкнутых 10

систем управления

Лекция 2

2.1.Работа САУ

2.1.1.Статические системы.

2.1.2.Астатические системы

Лекция 3

3.1.Обыкновенные линейные САУ

Лекция 4

4.1.Характеристики САУ

4.1.1. Передаточная функция.

4.1.2 Частотные характеристики.

4.1.3. Переходная функция.

Лекция 5

5.1.Типовые элементарные звенья (ТЭЗ)

Лекция 6

6.Способы соединения типовых элементарных звеньев (ТЭЗ)

6.1. 1.Последовательное соединение

6.1.2. Параллельное соединение звеньев

6.1.3.Общее правило записи передаточной функции замкнутой системы по любому из приложенных воздействий.

Лекция 7

7.1.Устойчивость САУ.Необходимые и достаточные условия устойчивости линейных САУ

7.2. Критерии устойчивости

7.2.1.Принцип аргумента.

7.2.2.Критерий устойчивости Михайлова

7.2.3.Критерий устойчивости Найквиста

7.2.4.Критерий устойчивости Гурвица

7.2.5.Критерий устойчивости Вышнеградского для систем третьего порядка

Лекция 8

8.1.Построение границы области устойчивости в пространстве параметров САУ (D-разбиение пространства параметров САУ)

Лекция 9

9.1. Качество систем автоматического управления

Лекция 10

10.1. Точность САУ на установившемся режиме

Лекция 11

11.1Повышение точности САУ

Лекция 12

12.1.Улучшение качества процессов регулирования

Лекция 13

13.1.Использование классических вариационных методов

Лекция 14

14.1.Импульсные системы

14.1.1.Импульсные фильтры.

14.1.2.Решетчатые функции

14.1.3.Конечно-разностные уравнения. Z-преобразования

14.2. Нелинейные САР

14.3. Критерий устойчивости В.Н.Попова

Лекция 1.

Введение.

Теория автоматического управления – прикладная наука, которая изучает принципы и методы построения автоматических систем, то есть систем, которые выполняют поставленные перед ними цели без участия человека

Если в контуре управления принимает участи человек, то такие системы называют автоматизированными системами.

ТАУ изучает управление определенными конкретными объектами управления.

Управление - организация определенного процесса, которая обеспечивает достижение определенной цели путем принятия соответствующих решений при выполнении определенных правил, алгоритмов, программ. Другими словами управление – процесс воздействия на объект управления с целью изменения его поведения в нужном направлении

Рассмотрим простейший пример. Предположим, что нам надо поддерживать постоянное давление в некотором объеме, добавляя в него газ для увеличения давления, и выпуская газ - для уменьшения давления.

 

Как организовать процесс управления в этом случае?

Цель управления – поддержание постоянного давления. Мы определим какое давление необходимо поддерживать (соберем информацию и будем ее хранить), измерим давление в объеме (также соберем информацию), сравним истинное давление с требуемым (переработаем информацию) и в зависимости от знака рассогласования (давление больше заданного или меньше) добавим газ или стравим его (примем решение и выполним его).

Принимая решения, система выполняет определенные правила, алгоритмы, программы.

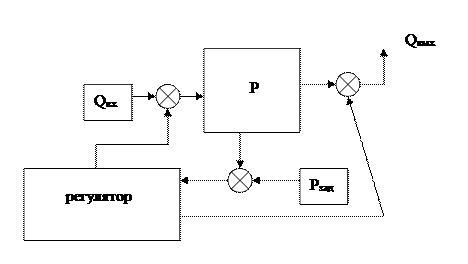
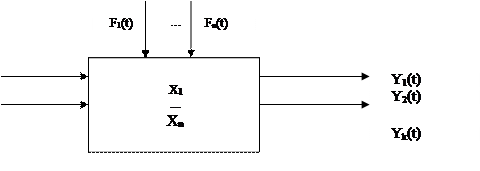
Объектом управления называется любое устройство, технологический процесс, производство, отрасль народного хозяйства и т.п., для которых ставится определенная задача (цель) управления, выражающаяся в заданном изменении множества фазовых координат или выходныхвеличин Y={ Y₁(t), Y₂(t),….Y_k(t) }, характеризующих изменение характеристик и свойств рассматриваемого объекта.

В общем виде структурная схема объекта управления имеет вид:

	U1(t)   U2(t)   Um(t)

 

Здесь–

- векторы соответственно управляющих воздействий, выходных параметров, возмущающих воздействий.

- переменные состояния, внутренние и часто недоступные измерению переменные, которые определяют состояние объекта в каждый момент времени, причем

Следует отметить, что все процессы управления происходят во времени (t), причем t – вещественная независимая переменная.

При изменении управляющих и возмущающих воздействий объект управления переходит из одного состояния в другое, причем множество состояний объекта управления дают необходимую информацию о характеристиках, условиях работы и свойствах рассматриваемого объекта.

Если у объекта много выходных величин (фазовых координат), то такой объект называется многомерным. Если из множества фазовых координат (выходных величин) в качестве регулируемой величины выбирается одна величина, то такой объект называется одномерным.

Структурная схема одномерного объекта управления имеет вид:

	U(t)

 

 

Многомерный объект управления может быть по структурной схеме приведен к одномерному, если множество регулируемых величин, управляющих и возмущающих воздействий представить в векторной форме.

 

Для управления объектом создается система автоматического управления.

САУ называется динамическая система, стремящаяся сохранить в допустимых пределах ошибки между требуемыми и действительными значениями регулируемых переменных при помощи их сравнения и использования полученных при этом сигналов для управления источниками энергии.

Поясним это определение.

САУ – динамическая системам, т. к процессы, происходящие в ней, изменяются во времени. При построении САУ используется принцип Ползунова, заключающийся в том, что действительное значение регулируемой величины сравнивается с её заданным (желаемым) значением. Полученный при этом сигнал используется для управления источниками энергии: в приведенном выше примере поддержания постоянного давления в резервуаре - для включения одного из клапанов.

Функциональную схему САУ в обобщенном виде можно представить:

 

 

Поведение любого ОУ характеризуется следующими параметрами:

1. X(t) – входная величина, которая может быть скалярной или векторной, она задает программу работы ОУ, то есть она показывает, как должен вести себя объект управления

2. Y(t) – регулируемая величина, векторная или скалярная величина, которая показывает как в действительности изменяется регулируемая величина.

Регулятор (управляющее устройство) - сравнивает выход ОУ с желаемым входным воздействием и в зависимости от результата вырабатывает управляющий сигнал (воздействие), который подается на вход объекта.

3. U(t) – управляющее воздействие, влияющее на объект управления и вызывающее изменение Y(t) в нужном направлении.

 

4. Возмущение f(t) - любое нежелательное воздействие, влияющее на ОУ.

5. Показатель точности работы САУ

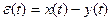
(-) - свидетельствует об ООС.

Показатель точности работы САУ – это один из важнейших критериев, определяющих качество работы САУ. Как сделать работу системы точной- этот вопрос вы будете изучать в нескольких дисциплинах, в том числе одна из дисциплин старшего курса будет целиком посвящена этому вопросу.

Теория автоматического управления решает две основные задачи – задачу анализа и задачу синтеза систем управления.

1.1. Задача синтеза включает в себя разработку и использование методов, которые позволяют выбрать схему САУ, выбрать элементы системы и их характеристики, определить характер взаимодействия между её элементами таким образом, чтобы проектируемая система удовлетворяла предъявляемым к ней требованиям.

Задача анализа включает в себя разработку и использование методов, которые позволяют по уже выбранной схеме системы, выбранным элементам и их характеристикам определить удовлетворяет ли спроектированная система предъявляемым к ней требованиям.

Следует отметить, что задачи синтеза и анализа в теории автоматического управления взаимосвязаны. Любая задача синтеза имеет свою предварительную историю и предпосылки, базирующиеся на предшествующих задачах анализа. Даже если объект управления имеет практически нулевую исходную информацию, для решения задачи синтеза делаются различные предположения, которые проверяются при решении задач анализа либо путем экспериментального исследования, либо путем математического моделирования. Обычно задача проектирования САУ осуществляется последовательным приближением к оптимальному варианту: сначала решается задача синтеза, затем – задача анализа, выявляются нежелательные моменты в работе САУ - снова решается задача синтеза и т.д. до получения желаемого результата.

Системы автоматического управления могут быть разомкнутыми и замкнутыми.

Рассмотрим примеры построения систем по разомкнутому и замкнутому циклам.

1. Разомкнутая система управления скоростью вращения вала двигателя постоянного тока.

 

Передвигая движок потенциометра Р, мы изменяем ток в цепи возбуждения (ОВ – обмотка возбуждения) генератора Г, что приводит к изменению его ЭДС и, следовательно, напряжения, подводимого к щеткам двигателя ДВ и скорости вращения вала двигателя. С валом двигателя связан тахогенератор (ТГ) - вспомогательный прибор, напряжение на выходе которого (V) пропорционально скорости вращения вала двигателя.

Это – разомкнутая система. Система называется разомкнутой, если в управляющем сигнале не содержится информации о результатах её работы.

В разомкнутой системе воздействие передается в одном направлении – от входа к выходу.

Схема рассматриваемой системы имеет вид:

 

Управление по разомкнутой схеме можно построить, базируясь на жестких характеристиках элементов, т.е., зная характеристики элементов, можно рассчитать, какому положению потенциометра соответствует определенная скорость вращения вала двигателя. Однако при работе системы изменяются температура, влажность, происходит старение элементов и т.д., что приводит к изменению их характеристик. Разомкнутая система – неточная система.

Скомпенсировать эти изменения можно с помощью замкнутой системы управления.

2. Замкнутая система управления скоростью вращения вала двигателя.

 

 

ОВ

V

ТГ

=

дв

Г

Е Дд

P

 

 

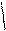
Привод постоянной

скорости

В замкнутой системе информация о результатах работы системы с её выхода подается на вход.

Передача сигнала с выхода на вход называется обратной св я зью.

Обратная связь, охватывающая все элементы системы,называется главной обратной связью. Если обратная связь охватывает один или несколько элементов – это местная обратная связь.

Главная обратная связь должна иметь такое направление, чтобы компенсировать изменение регулируемого параметра, вызванного возмущающим воздействием.

Пусть под действием возмущающего воздействия скорость вращения вала двигателя увеличилась. Для того, чтобы вернуть скорость к нужному значению (уменьшить), надо уменьшить ток через обмотку возбуждения.

Для этого надо из тока, протекающего через обмотку возбуждения, вычесть ток, создаваемый напряжением тахогенератора. Так как выходной сигнал вычитается из входного, то обратная связь называется отрицательной обратнойсвязью (ООС).

Главная обратная связь в САУ – всегда отрицательная.

Структурная схема замкнутой системы управления имеет вид:

 

Термин “обратная связь” был введен в 1906 г. Руммером в радиотехнике и сразу был использован в теории автоматического управления.

 

Сравнение эффективности работы разомкнутых и замкнутых

Систем управления

f

Количественную оценку преимущества замкнутых систем управления легко получить на примере линейного безинерционного управляемого объекта.

 

	u		y

Управляемый объект

 

 

Его уравнение имеет вид:

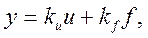
(1)

- коэффициент усиления объекта по сигналу управления,

- коэффициент усиления объекта по отношению к возмущающему воздействию.

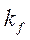Пусть >0 и >0.

Перед системой стоит задача воспроизведения входного сигнала х

сигналом у.

Сравним результаты работы разомкнутой и замкнутой систем.

Разомкнутая система.

f

Y

U

X

Управляемый объект

Регулятор

 

В разомкнутой системе при образовании сигнала управления U не учитывается информация о результатах её работы, т.е. не учитывается текущее значение Y.

Рассмотрим несколько вариантов.

I. Коэффициенты уравнения (1) известны точно, они стабильны и возмущение f(t)=0,

т.е. уравнение объекта

Пусть сигнал управления в разомкнутой системе

.

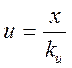
Тогда

и .

Таким образом, при отсутствии возмущающих воздействий и при стабильных коэффициентах усиления объекта разомкнутая система работает идеально точно.

Однако такие ситуации в реальной жизни не существуют.

На систему действуют возмущения и параметры системы не стабильны.

II. Коэффициенты известны точно и возмущение f(t) 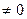. Про возмущение известно, что .

Поскольку поведение возмущения заранее не известно, выберем по-прежнему

.

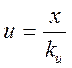Тогда в силу уравнения (1) имеем:

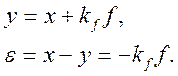
Таким образом, максимальная ошибка будет

Вывод: в разомкнутой системе при наличии возмущения и при стабильных коэффициентах будет ошибка при воспроизведении входного сигнала. У нас нет возможности повлиять на эту ошибку.

III. Возмущение отсутствует, т.е. f(t) ,

коэффициенты известны не точно и ошибка в определении .

Тогда уравнение объекта в действительности

а нам кажется, что .

Выбираем управление 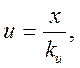т.к. считаем, что - истинное значение коэффициента усиления объекта по управлению.

Тогда

Отсюда

Если входной сигнал ограничен по модулю, т.е. 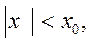то максимальное значение ошибки

Таким образом, и в этой ситуации, когда на систему не действует возмущение, но мы не точно знаем коэффициенты, в разомкнутой системе имеется ошибка.

Самое неприятное в ошибках, появляющихся в разомкнутых системах (случаи II и III), состоит в том, что у нас нет возможности воздействовать на них, т.к. они зависят от параметров, которыми мы не можем управлять: к_u и к _f – это характеристики объекта, f₀ – возмущение, - нестабильность коэффициента усиления объекта по управляющему воздействию.

f

Замкнутая система

	x		y
		u
			Управляемый объект

 

(-)

 

 

Объект тот же самый- описывается тем же уравнением:

 

(1)

Закон управления выбираем таким, чтобы он зависел от результата работы системы:

(2)

где коэффициент усиления регулятора, >0,

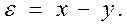(3)

Для получения уравнения замкнутой системы исключим из уравнений (1), (2), (3) и .

Тогда

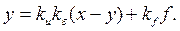
Обозначим

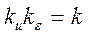- коэффициент усиления системы.

Отсюда

, (4)

и

. (5)

Рассмотрим те же три случая.

I. Коэффициенты известны точно и стабильны и

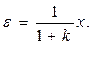
Этот результат хуже, чем у разомкнутой системы в этом случае.

Но если < , то увеличивая , а, следовательно, и , уменьшаем ошибку .

II .Коэффициенты известны точно и стабильны, При этом < .

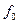Тогда .

Если в случае разомкнутой системы у нас не было возможности повлиять на величину , то в замкнутой системе увеличивая , можно уменьшить .

III. Возмущение отсутствует, т.е. , а коэффициенты нестабильны:

.

Тогда

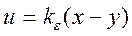
и .

Отсюда

и .

В этой ситуации также увеличивая , уменьшаем .

Таким образом, сравнивая работу разомкнутой и замкнутой систем,

видим, что в разомкнутой системе нет инструмента воздействия на ошибку. В замкнутой системе, изменяя параметры регулятора, можно уменьшать ошибку воспроизведения входного сигнала.