Улучшение качества процессов регулирования

Качество процессов регулирования определяется не только точностью на установившихся режимах работы, но и динамическими характеристиками переходных процессов, такими как длительность переходных процессов (быстродействие), колебательность и т.п. А эти динамические характеристики определяются запасом устойчивости системы, следовательно, надо увеличивать запас устойчивости.

Для повышения запаса устойчивости надо сначала попытаться изменить параметры системы (коэффициенты передачи отдельных звеньев, их постоянные времени). Если эти меры не помогают, надо идти на изменение структуры САУ, вводя в систему корректирующие устройства, которые должны изменить динамику САУ в нужном направлении.

Если корректирующее устройство (звенья) используется для придания системы устойчивости, увеличения запаса устойчивости, они называются демпфирующими или стабилизирующими. Термин корректирующие звенья- более широкий, они вводятся для изменения динамических свойств САУ.

Корректирующие звенья могут быть:

1. Последовательного типа

(1)

2. Параллельного типа

 

(2)

3. В виде местной обратной связи

 

(3)

Использование вида корректирующих звеньев определяется удобством технической реализации. Корректирующие звенья можно заменять одно другим так, что их динамические свойства будут оставаться неизменными, т.е. (4)

Если

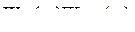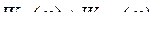= , отсюда

(5)

Если

,то

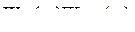= , отсюда

(6)

Аналогично можно получить:

(7)

(8)

(9)

(10)

Последовательные корректирующие звенья удобно применять там, где в регуляторе используется электрический сигнал. В этом случае корректирующее звено -цепочки.

Корректирующие звенья параллельного типа удобно применять в тех случаях, когда необходимо осуществить сложный закон управления с введением интеграла и производных от сигнала ошибки.

Корректирующие звенья в виде местной обратной связи нашли наиболее широкое распространение. Особенно отрицательные обратные связи, т.к. они ослабляют влияние нестабильности параметров, влияние нелинейностей.

Последовательные корректирующие звенья.

Это обычно пассивные (не содержат источников энергии) электрические цепи.

Рассмотрим примеры идеальных последовательных корректирующих звеньев и их характеристики.

Дифференцирующее звено.

 

Дифференциальное уравнение

,

здесь - постоянная времени дифференцирования,

- постоянная времени, характеризующая собственные динамические погрешности звена,

т.к. , то !!!!!

- коэффициент усиления звена.

 

Передаточная функция дифференцирующего звена:

.

Член (или ) осуществляет дифференцирование входного сигнала, причем на выходе имеется производная от входного сигнала, но и сам входной сигнал.

Правая часть дифференциального уравнения (или знаменатель передаточной функции) характеризует собственные динамические погрешности звена (его инерционные свойства).

Проанализируем соотношения этих эффектов.

. Это означает, что собственные динамические погрешности малы, а эффект дифференцирования – сильный.

- коэффициент усиления маленький, т.е. происходит ослабление входного сигнала.

На установившемся режиме

Как работает дифференцирующее звено.

На низких частотах: сопротивление - велико и низкие частоты через большое сопротивление плохо передаются на выход, т.е. коэффициент передачи дифференцирующей цепочки на низких частотах мал. Таким образом в спектре выходного сигнала низкие частоты имеют очень маленькие амплитуды. Вспомним, что низкие частоты определяют установившееся состояние. Следовательно, установившееся значение- сигал низкой величины. (Это видно и из соотношения )

На высоких частотах: сопротивление -мало и на выход проходят высокие частоты. Вспомним, что высокие частоты определяют фронт переходного процесса, т.е. увеличивают быстродействие процесса.

Таким образом, дифференцирующие цепочки подавляют низкие частоты и уменьшают установившееся значение выходной величины, т.е. уменьшают коэффициент усиления. С другой стороны, они увеличивают коэффициент передачи по высоким частотам и, следовательно, увеличивают быстродействие. Кроме того, дифференцирующие цепочки вносят положительный фазовый сдвиг, что повышает запас устойчивости.

Интегрирующее корректирующее звено.

Дифференциальное уравнение:

Передаточная функция

,

.

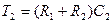В интегрирующем звене !!!!

Коэффициент усиления в интегрирующем звене изменяется по частотам.

Для пояснения работы этой цепочки рассмотрим её частотную характеристику

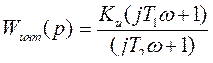
На частотах, где 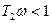(т.е на частотах и этим членом по сравнению с 1 в знаменателе можно пренебречь. Так как , то член и подавно меньше единицы и . Т.о. на -это усилительное звено.

На частотах (это низкие частоты) член и в члене уже можно пренебречь 1 и рассматривать = , т.е как интегрирующее звено. А т. к. , то на этих частотах и числитель равен 1.

На частотах (это более высокие частоты) член и в члене можно пренебречь 1 и в числителе появляется дифференцирующее звено.

Таким образом в диапазоне - это интегрирующее звено, а в диапазоне кроме интегрирования появляется эффект дифференцирования.

Напомним, что интегрирующее звено вносит фазовый сдвиг 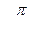, что плохо влияет на устойчивость. Вводится интегрирующее звено для повышения точности на установившемся режиме.

Параллельные корректирующие звенья

Как отмечалось, они вводятся при сложных законах управления с использованием интеграла и производной от ошибки.

Введение интеграла приводит к уменьшению установившейся ошибки, введение производной – повышает запас устойчивости.

Например,

В этих примерах – дифференцирование- идеальное.

Введение параллельных дифференцирующих устройств способствует поднятию высоких частот (т.к. сопротивление емкости на в.ч. – мало), а, следовательно, это улучшает динамику САУ.

Примером параллельного корректирующего устройства служит изодромное устройство.

Интегрирующее звено повышает точность на установившемся режиме, дифференцирующее звено – повышает коэффициент усиления на высоких частотах, что приводит к улучшению динамических свойств САУ.

Обратные связи.

Обратные связи могут быть положительными и отрицательными, а также жесткими и гибкими. Гибкая обратная связь (ГОС). ГОС называется такая связь, которая действует только в переходных режимах, а на установившемся

режиме как бы отключается.

На установившемся режиме , 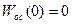и .

Пример ГОС.

.

На установившемся режиме и , как и в исходном апериодическом звене. Т.е. эта связь будет гибкой.

Жесткая обратная связь. (ЖОС)

Она действует не только в переходном режиме, но и в установившемся.

=

На установившемся режиме и , т.е. ЖООС действует и на установившемся режиме.

Если ЖООС – идеальное безинерционное звено, то

.

ЖООС уменьшает постоянную времени и коэффициент усиления в раз.

Расчетным путем наиболее просто определить параметры последовательного корректирующего звена, а реализовать проще обратные связи.

Положительные обратные связи (ПОС) находят меньшее использование, чем ООС.

= .

Если , то

Это изодромное звено, а оно, как известно, повышает астатизм системы. При этом в систему включено не интегрирующее звено, а инерционное, что меньше снижает запас устойчивости.

Однако, здесь точное выполнение затруднено.

 

 

Лекция 13

 

Использование классических вариационных методов

Пусть в качестве критерия качества рассматривается функционал вида

(1)

при заданных граничных условиях

и , (i=1,…,n)

В подинтегральное выражение (1) здесь не входят производные выше первой от координаты х₁ и управлений u_j. Если не наложено никаких ограничений, то х₁ и u_j принадлежат открытым областям.

Решение в этом случае дается уравнением Эйлера, записанным для всех координат и всех управлений, входящих в (1):

(2)

Где F’ – частные производные от подинтергальной функции (1) по соответствующим переменным. Это решение определяет группу интегральных кривых (экстремалей) , из которых необходимо выбрать траекторию, проходящую через заданную начальную и конечную точки.

При этом функции х_i и u_j должны принадлежать к так называемому классу функций С_2ai, т.е. должны иметь 2m непрерывных производных. В рассматриваемом случае (1) наивысшая производная является первой (m=1) и функция х_i, u_j должны иметь две непрерывные производные. Кроме того, для установления факта минимизации функционала (1) необходимо удостовериться, что вдоль экстремалей выполняются условия и . Эти условия аналогичны требованию положительности второй производной в точке минимума функции y=f(x).

Однако задача без ограничений не имеет смысл применительно к системе управления и регулирования. Введем ограничения в виде типа голономных связей

(3)

Ограничения типа неголономных (3) связей в виде дифференциальных уравнений

(4)

Ограничения на фазовые координаты и управления

(5)

Изопериметрические ограничения в виде функционалов

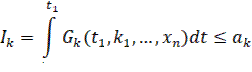
(6)

Тогда в уравнениях (2) вместо функции F должна называться функция

(7)

Где – произвольные множители Лагранжа, в общем случае зависящие от времени t. Это будет вариационная задача на так называемый условный экстремум (т.е. при наличии наложенных ограничений)

При учете связей в виде дифференциальных уравнений класс функций должен определяться по наивысшей производной выражения (7).

Если рассматривается одна переменная x(t), то функционал включает в себя производные x(t) более высоких порядков и имеет вид

(8)

то уравнения Эйлера будут иметь вид

(9)

Как и ранее, при наличии связей вместо функции F должна рассматриваться функция H, определяемая (7). Класс функций определяется по наивысшей производной (7) третьего порядка.

Следует отметить, что решение уравнений (2) и (3) часто приводит к корням характеристического уравнения, половина которых лежит в левой, а половина – в правой полуплоскости. Это наблюдается при использовании квадратичных функционалов и конечном времени регулирования .

Для устранения неустойчивости, которая получается в случае присоединения подобного регулятора к системе следует отбросить в решении те полюсы передаточной функции, которые лежат в правой полуплоскости. Это соответствует переходу к функционалу вида

(10)

т.е. бесконечному времени регулирования.

В этом случае искомые функции должны принадлежать к классу , причем производная третьего порядка может иметь разрыв первого рода в точке t=0.

При использовании изопериметрических ограничений типа (6) задача оптимизации решается так же в соответствии с уравнениями (7), но должна использоваться функция

(11)

где – производная постоянная множителя. В этом случае для определения произвольных постоянных и множителей к граничным условиям должна добавляться совокупность условий (6)

Пример. Объект управления описывается уравнением

(12)

где . Цепь управления заключается в переводе объекта из состояния при 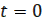в состояние при . В качестве критерия оптимальности (качества) примем минимум функционала

(13)

где – некоторый весовой коэффициент

Для функции (11)

Определим производные

(14)

Далее в соответствии с (9) находим

(15)

Совместное решение (12) и (15) дает характеристическое уравнение

(16)

Это уравнение содержит только четные степени р. Поэтому, если половина корней лежит в левой полуплоскости, то половина – в правой.

Положим . Тогда

(17)

Решение дает корни

(18)

Выражение для управляющей величины:

(19)

где и – произвольные постоянные.

Из краевых условий имеем

;

Если , то , а .

Тогда

 

 

Лекция 14

 

Импульсные системы

Литейной системой импульсного регулирования называется такая система автоматического регулирования, которая кроме звеньев, описываемых обыкновенными дифференциальными уравнениями, содержит импульсное звено, преобразующее непрерывное входное воздействие в равностоящие друг от друга импульсы.

В качестве импульсной системы можно также системы можно также рассматривать системы регулирования с управляющими цифровыми вычислительными машинами.

В общем случае импульсная линейная система регулирования будет содержать ряд непрерывных звеньев, описываемых ОДУ, и хотя бы одно прерывное – импульсное звено.

 

 

Рисунок

.

1

 

Рисунок 2.

Импульсным звеном может служить устройство типа ключа, которое по какой-то внешней причине производит замыкание цепи короткими импульсами через равные промежутки времени. На рисунке 2 представлены импульсные звенья трех типов.

В качестве импульсной системы можно рассматривать системы регулирования с управляющими ЭВМ. Дискретный характер получения и обработки информации в ЭВМ приводит к квантованию по времени, что позволяет применять здесь теорию импульсных систем (однако в упрощенных пределах).

Импульсные фильтры.

Рассмотрим случай, когда на выходе импульсного элемента импульсы отстоят друг от друга на одинаковые интервалы времени, продолжительность их так же одинаковая и они отличаются друг от друга только по амплитуде (тип 1 и 3)

Импульсная система может быть схематически представлена в виде соединения импульсного звена и непрерывной части.

Последовательность импульсов на выходе импульсного звена после прохождения через непрерывную часть, в следствие сглаживающих свойств последней и превращается в непрерывные величины на выходе.

Упрощенно импульсная система представлена на рисунке 3.

 

 

 

Импульсное звено на этой схеме изображено условно в виде ключа, который замыкается с периодом чередования Т. Если время замыкания ключа мало по сравнению с периодом чередования Т и постоянными времени непрерывной части и если сигнал на входе ключа в течение времени, когда он замкнут практически постоянен, то последовательность конечных по продолжительности импульсов на выходе ключа можно заменить последовательностью дельта-функций. Величина каждой дельта-функции (интеграла от нее времени) будучи пропорциональной значению сигнала на входе ключа в момент его замыкания.

Поскольку ключ замыкается в определенные моменты времени Т, 2Т, 3Т и тд. То сигнал на входе необходимо рассматривать именно в эти моменты времени, хотя на выходе непрерывной части сигнал и непрерывен, будем рассматривать его только в отдельные дискретные моменты времени.

Непрерывная часть совместно с ключом на ее входе будем называть импульсным фильтром.

 

 

 

Более строго импульсный фильтр следует определить как устройство, которое получает входные сигналы и одновременно дает выходные сигналы лишь в определенные моменты времени, например, Т, 2Т, 3Т и тд. На входе непрерывной части с передаточной функции дейтсвует дискретная функция x*[nT], где n = 0, ±1, ±2, ±3 и тд. В соответствии со сказанным эта функция может быть представлена в виде последовательности дельта-функций.

На выходе будет непрерывная функция, определяемая в эти же дискретные моменты времени: y(t)= y[nT], где n = 0, ±1, ±2, ±3 и тд.

Решетчатые функции.

Введем понятие решетчатой функции времени f [nT] или в сокращенной записи f[n], значения которой определены в дискретные моменты времени

Рисунок 5.

T=nT, где n – целое число, а Т – период повторения. Операция замены непрерывной функции решетчатой

(1)

Показана на рисунке 5.

 

Изображение на рисунке 5 (б) ординаты представляют собой так называемые дискреты исходной непрерывной функции f(t) при t=nT (рисунок 5). Дискреты f(t) могут быть определены для смещения моментов времени t=nT+ΔT=(n+Ԑ)T. Смещение ΔT=const могут быть положительной или отрицательной величиной при выполнении условия | ΔT|˂T.

Относительное смещение по модулю меньше единицы.

Образование смещенной решетчатой функции f[nT, ΔT], как в сокращенной записи f[n,Ԑ], из непрерывной функции f(t) для случая ΔT˃0 изображено на рисунке 5(в). В последующем будем считать n≥0 и Ԑ˃0. В случае необходимости рассмотрения функции f(n,Ԑ) с отрицательным параметром Ԑ˂0 дискретное время можно представить в виде 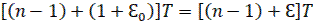. Тогда решетчатая функция может быть записана в виде f[n-1,Ԑ], где .

Введем понятие основной огибающей функции. Под основной огибающей будем понимать непрерывную функцию, совпадающую с заданными дискретами, которая может быть получена как результат решения дифференциального уравнения, порядок которого наименьший по сравнению с другими возможными огибающими, а для периодических решетчатых функций, кроме того выполняется требование минимальности значений частот гармоник. Так, например решетчатой функции могут соответствовать огибающие и (), где , 𝛋 – целое число, 𝛃 – любое число. Однако первая из них (основная огибающая) может быть получена в результате решения дифференциального уравнения первого порядка, тогда как вторая в результате решения дифференциального уравнения второго порядка.

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность

(2)

либо первая обратная разность

(3)

Обе эти разности показаны на рисунке 6

Рисунок 6.

Разновидности могут быть определены и для смещенных решетчатых функций .

Вследствие идентичности формул для Ԑ≠0 и Ԑ=0 принято, что Ԑ=0.

Прямая разность определяется в момент времени по будущему значению решетчатой функции при Это можно сделать в тех случаях, когда будущее значение известно.

Обратная разность определяется для момента времени по прошлому значению решетчатой функции в момент времени .

Аналогом второй производной непрерывной функции для решетчатой функции служат вторые разности: прямая

(4)

и обратная

(5)

Обратные разности обладают важной особенностью. Если решетчатая функция определена только для положительных значений аргумента, т.е. при n˂ 0, то в (1) n =0 прямая разность для любого целого положительного 𝛋.

Разностные уравнения.

В качестве аналогов дифференциальных уравнений можно рассматривать разностные уравнения (уравнения в конечных разностях)

При использовании прямых разностей неоднородные линейные разностные уравнения имеют вид:

, (6)

где – заданная, а - искомая решетчатая функция. При уравнение (6) становится однородным разностным уравнением, решением которого будет .

Разностное уравнение (6) может быть записано в другом виде

(7)

Коэффициенты этого уравнения определяются из зависимости

(8)

где биноминальные коэффициенты

(9)

При использовании обратных разностей уравнение в конечных разностях будет

(10)

или

(11)

Коэффициенты последнего уравнения определяются вложениями

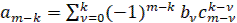(12)

(13)

Разностные уравнения можно рассматривать как рекурентные соотношения, позволяющие вычислить значения при n =0,1,2,… для заданных начальных значений , , и уравнения вида (7) при значении при n=0,1,2,… для заданных начальных значений , ,…, и уравнения вида (11). Также вычисления вечно минимизируются, а так же не представляют никаких принципиальных трудностей и при ручном счете даже в случае, когда коэффициенты разностных уравнений с течением времени и заменяются. Это отличает разностные уравнения от их непрерывных аналогов – дифференциальных уравнений.

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

(14)

где – корни характеристического уравнения

(15)

и – произвольные постоянные

Условие устойчивости:

Для исследования решений разностных уравнений в общем виде широко используются дискретные преобразования Лапласа, z – преобразование, 𝛚 – преобразование, а так же частотные методы.