Линеаризация дифференциальных уравнений САУ разложением в ряд Тейлора.

Пусть имеется САУ, на входе которой действует X(t), a на выходе Y(t). Пусть динамика этой системы описывается дифференциальным уравнением.

(3)

входная величина, выходная величина, производная.

Пусть в общем случае уравнение (3) нелинейное. При исследовании САУ мы хотим воспользоваться теорией обыкновенных линейных систем как наиболее простой.

Для этого линеаризуем дифференциальное уравнение (3).

Предположим, что в этой системе существует интересующий нас номинальный режим Y_ном.(t) соответствующий номинальному входному воздействию X_ном.(t) и номинальным начальным условиям:

(4)

Тогда уравнение САУ на номинальном режиме будет иметь вид:

(5)

Однако на практике бывает трудно выдержать номинальные начальные условия и в системе существуют некоторые отклонения от номинальных начальных условий. Т.е. реальные начальные условия имеют вид:

(6)

Тогда отклоненным начальным условиям (6) и тому же самому входному сигналу X_н(t) соответствует дифференциальное уравнение, описывающее этот отклоненный режим работы.

(7)

Обозначим 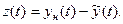(*) или

Если при любых начальных условиях (6), сколь угодно мало отличающихся от номинальных начальных условий (4), для любого моменте времени t > 0 будет малым |z(t)|, то номинальный режим Y_н(t) называется устойчивым.

Если при этом , то номинальный режим называется асимптотически устойчивым.

Для нахождения переходного процесса в САУ нам надо найти решение дифференциального уравнения (7).

С учетом (*) уравнение (7) можно записать в виде

(8)

Здесь все переменные являются функциями времени и t опущено только для простоты записи.

Разложим правую часть уравнения (8) в ряд Тейлора по степеням Z, Z⁽¹⁾, Z⁽ⁿ^-1).В разложении в ряд Тейлора учтем только производные от этих переменных не выше первого порядка

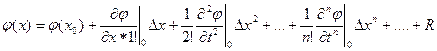
Если имеется функция нескольких переменных, то ряд Тейлора имеет вид

R- остаток ряда

o - точка разложения

Перед разложением правой части уравнения (8) в ряд Тейлора введем обозначения

Будем предполагать, что коэффициенты a_j не зависят от времени

С учетом этих обозначений уравнение (8) запишется в виде

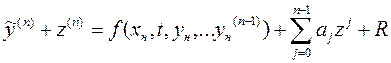(9)

Вычтем из уравнения (9) уравнение номинального режима (5) и пренебрежем членами высших порядков малости R. В результате получим

(10)

Уравнение (10) является линейным дифференциальным уравнением с постоянными коэффициентами. Процедура получения из нелинейного уравнения (3) линейного (10) называется линеаризацией. Иногда уравнение (10) записывается в форме Лагранжа:

Пример

Пусть в системе существует номинальный начальный режим:

Перепишем исходное уравнение:

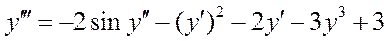
Учтем, что:

тогда

Определяем коэффициенты линеаризации

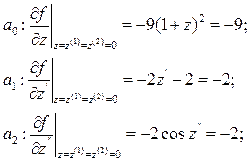
Линеаризованное уравнение, записанное в форме Лагранжа, будет иметь вид:

Отличия линеаризованного уравнения (10) от исходного нелинейного (3).

1. Уравнение (3) справедливо для всех режимов работы САУ, а уравнение (10) справедливо только при работе вблизи номинального режима (вблизи точки линеаризации).

2. Уравнение (3) является точным уравнением, а уравнение (10)- приближенным, т.к в процессе его вывода были отброшены члены высших порядков малости.

3. В уравнении (3) переменными являются полные величины y, y⁽¹⁾,y⁽²⁾ и т.д.

В уравнение (10) переменными являются отклонения этих переменных от номинального режима (от точки линеаризации). ∆ z, ∆z⁽¹⁾, ∆z⁽²⁾

4. Уравнение (3) является нелинейным, а уравнение (10) линейным дифференциальным уравнением с постоянными коэффициентами.

Геометрический смысл линеаризации разложением в ряд Тейлора.

Пусть имеется нелинейная функция F(x). Проведем линеаризацию этой функции в точке X_н

Разложим эту функцию в ряд Тейлора:

видим, что

Вычтем из F(x) номинальный режим и пренебрежем членами высших порядков малости R. Получим

Линеаризация разложением в ряд Тейлора геометрически означает перенос начала координат в точку линеаризации (в точку номинального режима) и замену нелинейной характеристики касательной к ней, проведенной в точке линеаризации.

Стандартная форма записи линеаризованного уравнения.

В теории автоматического управления принято линеаризованные дифференциальные уравнения записывать по следующим правилам:

1. В левой части уравнения записывается выходная величина и все ее производные, в правой части - входные величины и все их производные.

2. Производные выходной величины слева и входных справа записываются в порядке их убывания.

3. Принято, чтобы коэффициент перед выходной величиной был равен 1, если это не так, то все коэффициенты дифференциального уравнения делятся на коэффициент перед выходной величиной.

Пример

Опишем дифференциальным уравнением динамику цепи возбуждения генератора постоянного тока.

(1)

Здесь нелинейность – произведение входного и выходного параметров

Уравнение номинального режима

(2)

Линеаризуем уравнение (1):

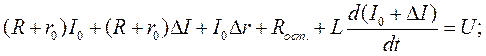(3)

(1-ый член- значение НЛ функции на установившемся режиме,

2-ой член- производная НЛ функции по

3-ий член – производная НЛ функции по

последний член – последний член уравнения (1) с учетом того, что

Вычтем из уравнения (3) уравнения номинального режима (2) и пренебрежем R_ост.

(4)

Приведем это уравнение к стандартной форме. Для этого члены с выходной величиной запишем в левой части уравнения, а члены с входной величиной -в правой

Обычно пишут так:

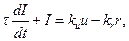считая, что

Лекция 4

Характеристики САУ

4.1.1. Передаточная функция.

4.1.2. Частотные характеристики.

4.1.3. Переходная функция.

Преобразование Лапласа.

Наиболее общей характеристикой, определяющей динамические свойства САУ, являются ее дифференциальные уравнения. Чтобы исследовать динамику САУ, надо найти решение дифференциальных уравнений (или одного дифференциального уравнения высокого порядка) для этой системы. Однако нахождение решений дифференциальных уравнений, особенно высокого порядка, связаны со значительными трудностями. Например, для нахождения постоянных, входящих в решение и зависящих от начальных условий, надо решить систему алгебраических уравнений. В теории управления получил распространение способ нахождения решения дифференциальных уравнений с использованием операторных методов.

Операционный способ, называемый преобразованием Лапласа, упрощает нахождение решений дифференциальных уравнений. Принцип этого метода сводится к следующему: к дифференциальному уравнению, в которое входит как аргумент время применяют прямое преобразование Лапласа. С помощью этого преобразования дифференциальное уравнение отображают на комплексную плоскость. В результате этого отображения дифференциальное уравнение преобразуется в алгебраическое, у которого аргументом является комплексная переменная где (вместо ).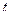

Полученное алгебраическое уравнение можно разрешить относительно интересующей нас регулируемой величиныY(p). Но полученное решение будет функцией комплексного переменного. Для получения решения Y(t), как функции от времени,Y(p) нужно преобразовать с помощью обратного преобразования Лапласа.

Каждой функции X(t) вещественной переменной t, которая называется оригиналом, ставится в соответствие по некоторому закону другая функция X(p), называемая изображением. Соответствие выбирается таким образом, чтобы сложным операциям над оригиналом соответствовали бы простые операции над изображением. Например, чтобы операции дифференцирования оригинала соответствовала бы операция умножения, операции интегрирования – операция деления. Такое соответствие задается прямым преобразованием Лапласа

Соответствие оригинала и изображения записывают

Для того, чтобы к функции X(t) можно было бы применить преобразование Лапласа, необходимо:

1) X(t) - была бы кусочно- непрерывной

3) X(t) должна обладать ограниченной скоростью роста

, где и не зависят от

Это означает, что X(t) должно расти медленнее, чем некоторая наперед заданная экспонента.

Имеются специальные таблицы для изображений элементарных функций.

Например:

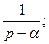
Напомним еще раз, что изображение является функцией комплексной переменной

Некоторые свойства преобразований Лапласа

1. Свойство линейности

Если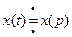

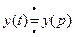и α и β произвольные числа, то

2. Теорема о дифференцировании оригинала

Если , то

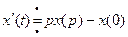, или в общем виде:

При отображении на комплексную плоскость дифференциального уравнения при нулевых начальных условиях

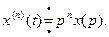
Дифференцирование оригинала при нулевых начальных условиях заменяется умножением изображения на в соответствующей степени.

1. Интегрирование оригинала

Если , то

Интегрирование оригинала соответствует делению на

4.Теорема запаздывания

Если и , то

5. Теорема о свертке

Свертке во множестве оригиналов соответствует обычное произведение функций во множестве изображений.

6. Теорема разложения

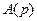Если где и - многочлены и порядок больше порядка , то оригинал

здесь - корни уравнения

7. В общем случае оригинал находится по изображению

Интегрирование производится вдоль прямой, параллельной мнимой оси и отстоящей от нее на произвольная константа, удовлетворяющая условию

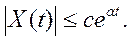
Пример решения дифференциального уравнения с помощью преобразования Лапласа.

Найти решение уравнения

Начальные условия (не нулевые)

Используя свойство линейности и теорему о дифференцировании оригинала, получаем

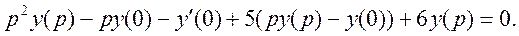
Отсюда

Для нахождения решения дифференциального уравнения применим теорему разложения.

У нас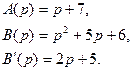

Корни уравнения

Тогда

4.1.1.ПЕРЕДАТОЧНЫЕ ФУНКЦИИ.

Задачи синтеза и анализа, а также исследование динамики САУ удобно решать, используя передаточные функции.

Пусть поведение системы описывается дифференциальным уравнением

(1)

x(t) – входная величина

y(t) – выходная величина

Отобразим это уравнение на комплексную плоскость, используя прямое преобразование Лапласа при нулевых начальных условиях, свойство линейности и теорему о дифференцировании оригинала.

Пусть ,

Получим

(2)

Таким образом отобразив дифференциальное уравнение с помощью преобразования Лапласа на комплексную плоскость, мы получим алгебраическое уравнение

Передаточной функцией называется отношение изображения Лапласа выходной величины к изображению Лапласа входной величины при нулевых начальных условиях.

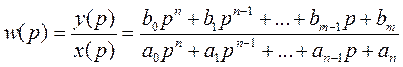
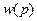всегда правильная дробь. Знаменатель передаточной функции ха-

рактеризует инерционные свойства САУ.

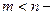условие физической осуществимости реальной САУ.

Знаменатель передаточной функции, приравненный к нулю, называется характеристическим уравнением

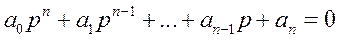
По передаточной функции можно найти установившееся значение выходной величины при подаче на вход единичного ступенчатого воздействия.

Используя предельные соотношения преобразования Лапласа, можно записать

- астатические системы,

- статические системы.

Например,

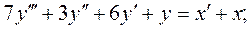
- астатическая система

Можно решать обратную задачу

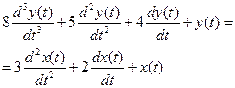
4.1.2.Свойства передаточных функций

Пусть - корни характеристического уравнения,

- корни полинома числителя.

Тогда

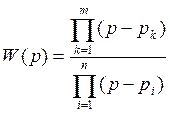
Если , то

Поэтому корни полинома числителя называются нулями передаточной функции.

Если , то

Поэтому корни полинома знаменателя, т.е. характеристического уравнения, называются полюсами передаточной функции.

Передаточная функция элемента с несколькими входами

Пусть на входе динамического элемента подаются сигналы а на выходе

Пусть динамика элемента описывается дифференциальным уравнением

Тогда

Отсюда

Коэффициенты перед 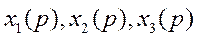называются передаточными функциями по отношению к соответствующим входам.

Изображение выходного сигнала элемента с несколькими входами равно сумме произведений изображений входов на передаточные функции по отношению к ним.

4.1.2.Частотные характеристики.

ЧХ могут быть получены из передаточной функции подстановкой

Получим частотную характеристику

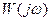- называется комплексной частотной характеристикой или амплитудно-фазочастотной характеристикой (АФЧХ).

Чтобы выделить из частотной характеристики действительную и мнимую части, нужно возвести в соответствующую степень. Напомним, что

j=j j³=-j

j²=-1 j⁴=1

Сделав приведение подобных, получим в числителе и знаменателе комплексное число. Умножим числитель и знаменатель на число, комплексно-сопряженное знаменателю. В результате в числителе получим комплексное число, а в знаменателе - действительное число. Разделив действительную часть числителя на знаменатель, получим . Разделив мнимую часть числителя на знаменатель, получим .

Рассмотрим пример.

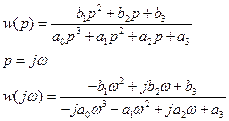
Сделаем приведение подобных

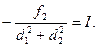
Как всякое комплексное число 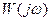можно записать

где

-амплитудно –частотная характеристика (АЧХ)- показывает как изменяется амплитуда выходного сигнала (при постоянной амплитуде входного сигнала) при изменении частоты входного сигнала.

- фазо- частотная характеристика (ФЧХ)- показывает как изменяется фаза выходного сигнала по отношению к фазе входного сигнала при изменении частоты входного сигнала.

По АЧХ и ФЧХ можно построить АФЧХ

4.1.3.Переходная функция.

Это реакция системы на единичное ступенчатое воздействие.

Лекция 5

5.1.Типовые элементарные звенья (ТЭЗ)

Изучая дифференциальные уравнения элементов САУ, можно заметить, что разные по физической природе элементы описываются одинаковыми дифференциальными уравнениями.

Для упрощения представления характеристик элементов САУ, обладающих одинаковыми динамическими свойствами и описываемых одинаковыми дифференциальными уравнениями, вводят понятие типового элементарного звена (ТЭЗ). Любой элемент САУ может быть описан ТЭЗ или их комбинацией.

Под ТЭЗ понимают элемент, динамические процессы в котором описываются дифференциальным уравнением не выше второго порядка и который обладает направленностью действия, т.е. сигнал в нем проходит только от входа к выходу.

ТЭЗ- это математическая абстракция, которая вводится для упрощения анализа и синтеза САУ.

Звено нулевого порядка

(Усилительное, пропорциональное, безинерционнное)

Уравнение этого звена

Операторная форма записи

Статическая характеристика

Структурная схема этого звена

Частотная характеристика

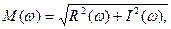
Таким звеном описываются:

1) потенциометр без учета массы подвижных элементов

2) электронный усилитель без учета собственных динамических погрешностей

3) редуктор без учета люфта

4) многие датчики (температуры, давления и т.д.)

В реальных условиях таких звеньев не существует, к ним можно только приблизиться в определенных условиях.

Звено первого порядка.

(инерционное звено, апериодическое звено)

Дифференциальное уравнение этого звена

Такими уравнениями описываются:

· генератор постоянного тока,

· нагревательная печь.

Уравнения статики (статическая характеристика)

Операторная форма записи дифференциального уравнения

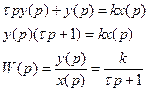
Характеристическое уравнение

Структурная схема звена

Решение дифференциального уравнения - экспонента

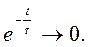
За : т.е. экспонента достигнет 95%.

Частотная характеристика

Получим частотную характеристику из передаточной функции, для чего подставим в нее

Звено 2-го порядка.

Дифференциальное уравнение

- постоянная времени,

- коэффициент усиления,

- степень демпфирования.

Статическая характеристика.

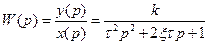
Характеристическое уравнение

Если , то корни зависят от

1) 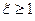Оба корня – вещественные.

2) Корни комплексно-сопряженные

3) Корни чисто мнимые

Структурная схема звена

Случай 1) –апериодическое звено 2-го порядка (генератор постоянного тока при 4Т_яТ_м, где Т_я- постоянная времени якорной цепи, 4Т_я-электромеханическая постоянная времени.

Случай 2) – колебательное звено (движение массы при наличии сил упругости, RLC- контур, движение маятника).

Случай 3) – консервативное звено (LC- контур, R=0).

Все характеристики звена зависят от , частотные характеристики тоже зависят от

Интегрирующее звено.

Дифференциальная форма записи интегрирующего звена.

Смысл этого уравнения - скорость изменения выходной величины пропорциональна входной величине.

Возьмем интеграл от обеих частей уравнения и перепишем его в виде:

, тогда

Это интегральная форма записи интегрирующего звена.

Смысл этого уравнения - выходная величина пропорциональна интегралу от входной величины.

Например, пусть Q- расход жидкости.

Тогда масса накопленной жидкости

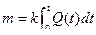
Операторная форма записи дифференциального уравнения интегрирующего звена:

Структурная схема звена

Частотная характеристика.

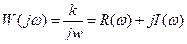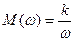
Дифференцирующее звено

Дифференциальное уравнение звена:

Выходная величина пропорциональна скорости изменения входной величины.

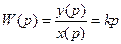
Структурная схема.

Частотные характеристики.

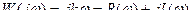
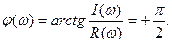
Так как дифференцирующее звено имеет положенный сдвиг фаз (),

т.е. выходной сигнал на опережает входной сигнал, то при включении этого звена в САУ суммарный сдвиг фаз уменьшается, что улучшает процесс управления.