Счисление сложение в двоичной системе счисления осуществляется по правилам
| 0 + 0 = 0 | 0 + 1 = 1 | 1 + 0 = 1 | 1 + 1 = 210 = 102 (единица идет в старший разряд) |
Таблица вычитания в двоичной системе счисления имеет вид
| 0 – 0 = 0 | 1 – 0 = 1 | 1 – 1 = 0 | 0 – 1 = 102 | 102 – 1 = 1 (единицу забираем у старшего разряда) |
Таблица умножения в двоичной системе счисления имеет вид
| 0 x 0 = 0 | 0 x 1 = 0 | 1 x 0 = 0 | 1 x 1 = 1 |
Таблица деления в двоичной системе счисления имеет вид
| 0: 0 не определено | 1: 0 не определено | 0: 1 = 0 | 1: 1 = 1 |
Обратным кодом числа в системе с основанием р называется число в этой системе, получаемое заменой цифры, символа в каждом разряде числа на его дополнение до максимальной цифры в системе (то есть до р – 1).
Дополнительный код = обратный код + единица в младшем разряде.
Пример.
1. 10011 Þ двоичное число,
01100 Þ обратный код этого двоичного числа,
01101 Þ дополнительный код этого двоичного числа;
2. 457 Þ восьмеричное число,
321 Þ дополнительный код;
3. А9 Þ шестнадцатеричное число,
57 Þ дополнительный код.
Вычитание с помощью дополнительного кода: найти дополнительный код вычитаемого такой же разрядности, как и уменьшаемое, и сложить этот код с уменьшаемым. Результатом вычитания будет полученная сумма без учета старшего разряда (отбрасывается).
Пример. Выполним вычитание напрямую и через сложение (через дополнительный код):
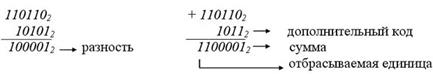
ПРИМЕРЫТИПОВЫХ РЕШЕНИЙ
Задача № 1
Даны два числа a=D716 и b=3318. Необходимо определить какое из чисел, записанных в двоичной системе счисления, удовлетворяет неравенству a<c<b?
1) 110110012
2) 110111002
3) 110101112
4) 110110002
Общий подход: перевести все числа (и исходные данные, и ответы) в одну (любую!) систему счисления и сравнить.
|
|
Решение (вариант 1, через десятичную систему):
1) 
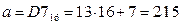
2) 
3) Переводим в десятичную систему все ответы:
110110012 = 217,
11011100 2= 220,
110101112 = 215,
110110002=216
4) Очевидно, что между числами 215 и 217 может быть только 216
5) Таким образом, верный ответ – 4.
Решение (вариант 2, через двоичную систему):
1) 
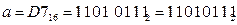(каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду);
2) 
(каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать);
3) Теперь нужно сообразить, что между этими числами находится только двоичное число 110110002 – это ответ 4.
Решение (вариант 3, через восьмеричную систему):
1) 
(сначала перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной);
2) 
, никуда переводить не нужно;
3) Переводим в восьмеричную систему все ответы:
110110012 = 011 011 0012 = 3318 (разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, как в п. 1)
11011100 2= 3348, 110101112 = 3278, 110110002=3308
4) В восьмеричной системе между числами 3278 и 3318 может быть только 3308
5) Таким образом, верный ответ – 4.
Решение (вариант 4, через шестнадцатеричную систему):
1) 
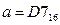никуда переводить не нужно;
2) 
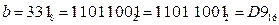(сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F);
|
|
3) Переводим в шестнадцатеричную систему все ответы:
110110012 = 1101 10012 = D916 (разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F, как в п. 1)
11011100 2= DC16, 110101112 = D716, 110110002=D816
4) В шестнадцатеричной системе между числами D716 и D916 может быть только D816
5) Таким образом, верный ответ – 4.
Задача № 2
Даны два числа х и у. Чему равна сумма этих чисел, если 
и 
?
1) 1218
2) 1718
3) 6916
4) 10000012
Общий подход: перевести оба исходных числа и ответы в одну (любую!) систему счисления, и выполнить сложение
Решение (вариант 1, через десятичную систему):
1. 
2. 
3. Сложение: 35 + 86 = 121.
4 а) переводим результат во все системы, в которых даны ответы (пока не найдем нужный):
121 = 11110012 = 1718 = 7916
4 б) или переводим все ответы в десятичную систему
1218 = 81,
1718 = 121,
6916 = 105,
10000012 = 65.
5) Таким образом, верный ответ – 2.
Решение (вариант 2, через двоичную систему):
1) 
(каждая цифра восьмеричной системы отдельно переводится в три двоичных – триаду, старшие нули можно не писать).
2) 
(каждая цифра шестнадцатеричной системы отдельно переводится в четыре двоичных – тетраду).
3) Складываем
1000112
+ 10101102.
11110012
4) Переводим все ответы в двоичную систему
1218 = 001 010 0012 = 10100012 (по триадам)
1718 = 001 111 0012 = 11110012 (по триадам)
6916 = 0110 10012 = 11010012 (по тетрадам)
10000012 не нужно переводить.
5) Правильный ответ – 2.
Решение (вариант 3, через восьмеричную систему):
1) , никуда переводить не нужно
2) 
(сначала
перевели в двоичную систему, потом двоичную запись числа разбили на триады справа налево, каждую триаду перевели отдельно в десятичную систему, так как для чисел от 0 до 7 их восьмеричная запись совпадает с десятичной)
|
|
3) Складываем
438
+ 1268 .
1718
4) Видим, что такой ответ есть, это ответ 2.
Решение (вариант 4, через шестнадцатеричную систему):
1) 
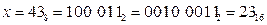(сначала перевели в двоичную систему, потом двоичную запись числа разбили на тетрады справа налево, каждую тетраду перевели в шестнадцатеричную систему; при этом тетрады можно переводить из двоичной системы в десятичную, а затем заменить все числа, большие 9, на буквы – A, B, C, D, E, F).
2) 
, никуда переводить не нужно.
3) Складываем
2316
+ 5616 .
7916
4) Переводим в шестнадцатеричную систему все ответы:
1218 = 001 010 0012 = 0101 00012 = 5116 (перевели в двоичную систему по триадам, разбили на тетрады справа налево, каждую тетраду перевели отдельно в десятичную систему, все числа, большие 9, заменили на буквы – A, B, C, D, E, F).
171 2 = 001 111 0012 = 0111 10012 = 7916,
6916, переводить не нужно
10000012 = 0100 00012 = 4116 .
5) Таким образом, верный ответ – 2.
Задача № 3
Пример 1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
– вспомним алгоритм перевода числа из десятичной системы в систему с основанием 
, из него следует, что младшая цифра результата – это остаток от деления исходного числа на , а две младших цифры – это остаток от деления на 
и т.д.;
– в данном случае 
, остаток от деления числа на 
должен быть равен 114 = 5;
– потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16.
Решение (вариант 1, через десятичную систему):
1. Общий вид чисел, которые дают остаток 5 при делении на 16:
где 
– целое неотрицательное число (0, 1, 2, …)
2. Среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при 
) и 21 (при 
).
3. Таким образом, верный ответ – 5, 21.
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
1) Переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения.
2) Из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
3) Таким образом, верный ответ – 5, 21.
Пример 2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход:
– здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через N;
– поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть N > 2;
– вспомним алгоритм перевода числа из десятичной системы в систему с основанием (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на N.
Решение:
1) Итак, нужно найти все целые числа 
, такие, что остаток от деления 23 на равен 2, или (что то же самое)
(*)
где – целое неотрицательное число (0, 1, 2, …).
2) Сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа.
3) Из формулы (*) получаем 
, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2.
4) В этой задаче есть только три таких делителя: 
и 21.
5) Таким образом, верный ответ – 3, 7, 21.
Задача № 4.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.
Общий подход:
– неизвестно основание системы счисления, мы обозначим его через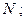 
– пока будем считать, что запись числа 31 в системе с основанием состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через ) нужно найти:
2 1 0 ← разряды
31 = k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1;
– можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как 
при некотором целом ; например, для числа с пятью разрядами получаем:
4 3 2 1 0 ← разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0
= k·N2 + N + 1
для 
(из первых трех слагаемых вынесли общий множитель ).
Решение:
1) Итак, нужно найти все целые числа 
, такие что
(**)
где – целое неотрицательное число (0, 1, 2, …).
2) Сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа.
3) Из формулы (**) получаем 
, так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, 
– целое число.
4) Выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30.
5) Из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0).
6) Таким образом, верный ответ – 2, 3, 5, 30.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Задача № 1
Вариант №1
Как представлено число 8310 в двоичной системе счисления?
1) 10010112
2) 11001012
3) 10100112
4) 1010012
Вариант №2
Сколько единиц в двоичной записи числа 195?
1) 5
2) 2
3) 3
4) 4
Вариант №3
Сколько единиц в двоичной записи числа 173?
1) 7
2) 5
3) 6
4) 4
Вариант №4
Как представлено число 25 в двоичной системе счисления?
1) 10012
2) 110012
3) 100112
4) 110102
Вариант №5
Как представлено число 82 в двоичной системе счисления?
1) 10100102
2) 10100112
3) 1001012
4) 10001002
Вариант №6
Как представлено число 263 в восьмеричной системе счисления?
1) 3018
2) 6508
3) 4078
4) 7778
Вариант №7
Как записывается число 5678 в двоичной системе счисления?
1) 10111012
2) 1001101112
3) 1011101112
4) 111101112
Вариант №8
Как записывается число A8716 в восьмеричной системе счисления?
1) 4358
2) 15778
3) 52078
4) 64008
Вариант №9
Как записывается число 7548 в шестнадцатеричной системе счисления?
1) 73816
2) 1A416
3) 1EC16
4) A5616
Вариант №10
Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?
1) 1
2) 2
3) 3
4) 4
Вариант №11
Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-35)?
1) 3
2) 4
3) 5
4) 6
Вариант №12
Дано: 
, 
. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству 
?
1) 10011010
2) 10011110
3) 10011111
4) 11011110
Вариант №13
Дано: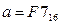 
, 
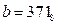. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 11111001
2) 11011000
3) 11110111
4) 11111000
Вариант №14
Дано: 
, 
. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 11011010
2) 11111110
3) 11011110
4) 11011111
Вариант №15
Дано: 
, 
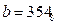. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 11101010
2) 11101110
3) 11101011
4) 11101100
Вариант №16
Дано: 
, 
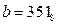. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 11101010
2) 11101000
3) 11101011
4) 11101100
Вариант №17
Дано: а =D716, b =3318. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 11011001
2) 11011100
3) 11010111
4) 11011000
Вариант №18
Дано: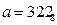 
, 
. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 11010011
2) 11001110
3) 11001010
4) 11001100
Вариант №19
Дано: , . Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству ?
1) 10011010
2) 10011110
3) 10011111
4) 11011110
Вариант №20
Как представлено число 18910 в двоичной системе счисления?
1) 10010112
2) 11001012
3) 10100112
4) 101111012
Задача № 2
Вариант №1
Вычислите сумму чисел x и y, при x = A616, y = 758. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111000112
4) 100100112
Вариант №2
Значение выражения 1016 + 108 • 102 в двоичной системе счисления равно
1) 10102
2) 110102
3) 1000002
4) 1100002
Вариант №3
Вычислите сумму двоичных чисел x и y, если x = 10101012 и y = 10100112
1) 101000102
2) 101010002
3) 101001002
4) 101110002
Вариант №4
Вычислите значение суммы 102 + 108 +1016 в двоичной системе счисления.
1) 101000102
2) 111102
3) 110102
4) 101002
Вариант №5
Вычислите сумму чисел x и y, при x = 2718, y = 111101002. Результат представьте в шестнадцатеричной системе счисления.
1) 15116
2) 1AD16
3) 41216
4) 10B16
Вариант №6
Вычислите сумму чисел x и y, при x = A116, y = 11012. Результат представьте в десятичной системе счисления.
1) 204
2) 152
3) 183
4) 174
Вариант №7
Вычислите сумму чисел x и y, при x = 568, y = 11010012. Результат представьте в двоичной системе счисления.
1) 111101112
2) 100101112
3) 10001112
4) 110011002
Вариант №8
Вычислите сумму чисел x и y, при x = 5A16, y = 10101112. Результат представьте в восьмеричной системе счисления.
1) 1518
2) 2618
3) 4338
4) 7028
Вариант №9
Вычислите сумму чисел x и y, при x = 1278, y = 100101112. Результат представьте в десятичной системе счисления.
1) 214
2) 238
3) 183
4) 313
Вариант №10
Вычислите A8116 + 37716. Результат представьте в той же системе счисления.
1) 21B16
2) DF816
3) C9216
4) F4616
Вариант №11
Чему равна разность чисел 10116 и 1101112?
1) 3128
2) 128
3) 3216
4) 6416
Вариант №12
Чему равна разность чисел 1248 и 5216?
1) 112
2) 102
3) 1002
4) 1102
Вариант №13
Чему равна сумма чисел 278 и 3416?
1) 1138
2) 638
3) 5116
4) 1100112
Вариант №14
Чему равна сумма чисел 438 и 5616?
1) 7916
2) A316
3) 1258
4) 10101012
Вариант №15
Чему равна сумма чисел 438 и 5616?
1) 1218
2) 1718
3) 6916
4) 10000012
Вариант №16
Вычислите сумму чисел X и Y, если X=1101112 Y=1358. Результат представьте в двоичном виде.
1) 110101002
2) 101001002
3) 100100112
4) 100101002
Вариант №17
Вычислите сумму чисел x и y, при x = B816, y = 778. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111101112
4) 100100112
Вариант №18
Вычислите сумму чисел x и y, при x = F616, y = 358. Результат представьте в двоичной системе счисления.
1) 110110112
2) 111100012
3) 111000112
4) 1000100112
Вариант №19
Чему равна сумма чисел 538 и 6616?
1) 1278
2) 3728
3) 6916
4) 100100012
Вариант №20
Чему равна разность чисел 110116 и 11011112?
1) 3128
2) 1228
3) 32A16
4) 117016
Задача № 3
Вариант №1
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Вариант №2
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Вариант №3
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Вариант №4
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Вариант №5
В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Вариант №6
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
Вариант №7
В системе счисления с некоторым основанием число десятичное 25 записывается как 100. Найдите это основание.
Вариант №8
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
Вариант №9
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?
Вариант №10
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?
Вариант №11
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Вариант №12
Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
Вариант №13
Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
Вариант №14
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
Вариант №15
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
Вариант №16
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие25, запись которых в системе счисления с основанием четыре оканчивается на 11.
Вариант №17
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Вариант №18
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Вариант №19
В системе счисления с некоторым основанием число десятичное 129 записывается как 1004. Найдите это основание.
Вариант №20
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10,11,12,, …, 17 в системе счисления с основанием 5.
Задача № 4
Переведите данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Вариант №1
а) 860(10);
б) 785(10);
в) 149,375(10);
г) 953,25(10);
д) 228,79(10).
Вариант №2
а) 250(10);
б) 757(10);
в) 711,25(10);
г) 914,625(10);
д) 261,78(10).
Вариант №3
а) 759(10);
б) 265(10);
в) 79,4375(10);
г) 360,25(10);
д) 240,25(10).
Вариант №4
а) 216(10);
б) 336(10);
в) 741,125(10);
г) 712,375(10);
д) 184,14((10).
Вариант №5
а)530(10);
б) 265(10);
в) 597,25(10);
г) 300,375(10);
д) 75,57(10).
Вариант №6
а) 945(10);
б) 85(10);
в) 444,125(10);
г) 989,375(10);
д) 237,73(10).
Вариант №7
а) 287(10);
б) 220 (10);
в) 332,1875(10);
г) 652,625(10);
д) 315,21(10).
Вариант №8
а) 485(10);
б) 970 (10);
в) 426,375(10);
г) 725,625(10);
д) 169,93(10).
Вариант №9
а) 639(10);
б) 485(10);
в) 581,25(10);
г) 673,5(10);
д) 296,33(10).
Вариант №10
а) 618(10);
б) 556(10);
в) 129,25(10);
г) 928,25(10);
д) 155,45(10).
Вариант №11
а) 772(10);
б) 71(10);
в) 284,375(10);
г) 876,5(10);
д) 281,86(10).
Вариант №12
а) 233(10);
б) 243(10);
в) 830,375(10);
г) 212,5(10);
д) 58,89(10).
Вариант №13
а) 218(10);
б) 767(10);
в) 894,5(10);
г) 667,125(10);
д) 3,67(10).
Вариант №14
а) 898(10);
б) 751(10);
в) 327,375(10);
г) 256,625(10);
д) 184,4(10).
Вариант №15
а) 557 (10);
б) 730 (10);
в) 494,25 (10);
г) 737,625 (10);
д) 165,37 (10).
Вариант №16
а) 737 (10);
6) 92 (10);
в) 934,25 (10);
г) 413,5625 (10);
д) 100,94 (10).
Вариант №17
a) 575 (10);
б) 748 (10);
в) 933,5 (10);
г) 1005,375 (10);
д) 270,44 (10).
Вариант №18
а) 563 (10);
б) 130 (10);
в) 892,5 (10);
г) 619,25 (10);
д) 198,05 (10).
Вариант №19
а) 453 (10);
б) 481 (10);
в) 461,25 (10);
г) 667,25(10);
д) 305,88 (10).
Вариант №20
а) 949 (10);
б) 763 (10);
в) 994,125 (10);
г) 523,25 (10);
д) 203,82 (10).
Задача № 5
Переведите данное число в десятичную систему счисления.
Вариант №1
а) 1001010(2);
б) 1100111(2);
в) 110101101,00011(2);
г) 111111100,0001(2);
д) 775,11(8);
е) 294,3(16).
Вариант №2
а) 1111000(2);
б) 1111000000(2);
в) 111101100,01101(2);
г) 100111100,1101(2);
д) 1233,5(8);
е) 2B3,F4(I6).
Вариант №3
а) 1001101(2);
б) 10001000(2);
в) 100111001,01(2);
г) 1111010000,001(2);
д) 1461,15(8);
е) 9D,A(16)
Вариант №4
а) 1100000110(2);
б) 1100010(2);
в) 1011010,001(2);
г) 10101000,001(2);
д) 1537,22(8);
е) 2D9,8(16).
Вариант №5
а) 101000111(2);
б) 110001001(2);
в) 1001101010,01(2);
г) 1011110100,01(2);
д) 1317,75(8);
е) 2F4,0С(16).
Вариант №6
а) 110001111(2);
б) 111010001(2);
в) 100110101,001(2);
г) 10000010,01011(2);
д) 176,5(8);
е) 3D2,04(16).
Вариант №7
а) 10101000(2);
б) 1101100(2);
в) 10000010000,01001(2);
г) 1110010100,001(2);
д) 1714,2(8); е) DD,3(16).
Вариант №8
а) 10101000(2);
б) 101111110(2);
в) 1010101,101(2);
г) 1111001110,01(2);
д) 721,2(8);
е) 3С9,8(16).
Вариант №9
а) 1011000011(2);
б) 100010111(2);
в) 1100101101,1(2);
г) 1000000000,01(2);
д) 1046,4(8);
е) 388,64(16).
Вариант №10
а) 1000001111(2);
б) 1010000110(2);
в) 101100110,011011(2);
г) 100100110,101011(2);
д) 10232,2(8);
е) 53,9(16).
Вариант №11
а) 1001101111(2);
б) 1000001110(2);
в) 111110011,011(2);
г) 11010101,1001(2);
д) 1634,5(8);
е) C2,3(16).
Вариант №12
а) 1111100010(2);
б) 1000011110(2);
в) 101100001,011101(2);
г) 1001111001,1(2);
д) 1071,54(8);
е) 18B,0C(16).
Вариант №13
а) 101110100(2);
б) 1111101101(2);
в) 1110100001,01(2);
г) 1011111010,0001(2);
д) 744,12(8);
е) 1ЕЕ,С(16).
Вариант №14
а) 101001101 (2);
б) 1110111100 (2);
в) 10000001000,001 (2);
г) 1000110110,11011 (2);
д) 147,56 (8);
е) 1СА,3 (16).
Вариант №15
а) 1110000010 (2);
6) 1000100 (2);
в) 110000100,001 (2);
г) 1001011111,00011(2);
д) 665,42 (8);
е) 246,18(,6).
Вариант №16
а) 1010000 (2);
б) 10010000 (2);
в) 1111010000,01 (2);
г) 101000011,01 (2);
д) 1004,1 (8);
е) 103,8С (16).
Вариант №17
а) 11100001 (2);
б) 101110111 (2);
в) 1011110010,0001 (2);
г) 1100010101,010101(2);
д) 533,2 (8);
е) 32,22 (16).
Вариант №18
а) 111001010 (2);
б) 1101110001 (2);
в) 1001010100,10001 (2);
г) 111111110,11001(2);
д) 1634,35 (8);
е)6В,А (16).
Вариант №19
а) 1110001111 (2);
б) 100011011 (2);
в) 1001100101,1001 (2);
г) 1001001,011 (2);
д) 335,7 (8);
е) 14C,A (16).
Вариант №20
а) 1100010010 (2);
б) 10011011 (2);
в) 1111000001,01 (2);
г) 10110111,01 (2);
д) 416,1(в>; е) 215,7 (16).
Задача № 6
Выполните арифметические действия.
Вариант №1
1.
a) 1101100000(2) + 10110110(2);
b) 101110111(2) + 1000100001(2);
c) 1001000111,01(2) + 100001101,101(2);
d) 271,34(8) + 1566,2(8);
e) 65,2(16) + ЗСА,8(16).
2.
a) 1011001001(2) -1000111011(2);
b) 1110000110(2) -101111101(2);
c) 101010000,10111(2) -11001100,01(2);
d) 731,6(8) - 622,6(8);
e) 22D,l(l6) -123,8(16).
3.
a) 1011001(2) х 1011011(2);
b) 723,l(8) х 50,2(8) ;
c) 69,4(16) х А,В(16).
Вариант №2
1.
а) 1010101(2) + 10000101(2);
б) 1111011101(2) + 101101000(2);
в) 100100111,001(2) + 100111010,101(2);
г) 607,54(8) + 1620,2(8);
д) 3BF,A(16) + 313,А(16).
2.
а) 1001000011(2) -10110111(2);
б) 111011100(2) -10010100(2);
в) 1100110110,0011(2)-11111110,01(2);
г) 1360,14(8) -1216,4(8);
д) 33B,6(16)- 11В,4(16).
3.
а) 11001(2) х 1011100(2);
б) 451,2(8) х 5,24(8);
в) 2В,А(16) х 36,6(16).
Вариант №3
1.
а) 100101011(2) + 111010011(2);
б) 1001101110(2)+ 1101100111(2);
в) 1010000100,1(2) + 11011110,001(2);
г) 674,34(8) + 1205,2(8);
д) 2FE,6(16) + ЗВ,4(16).
2.
а) 1100110010(2) - 1001101101(2);
б) 1110001100(2) -10001111(2);
в) 11001010,01(2) -1110001,001(2);
г) 641,6(8) - 273,04(8)
д) ЗСЕ,В8(16) - 39А,В8(16).
3.
а) 1010101(2) * 1011001(2);
б) 1702,2(8) * 64,2(8);
в) 7,4(16)* 1D4(16)
Вариант №4
1.
а) 101111111(2) + 1101110011(2);
б) 10111110(2)+ 100011100(2);
в) 1101100011,0111(2) + 1100011,01(2);
г) 666,2(8) + 1234,24(8);
д) 346,4(16) + ЗF2,6(16).
2.
а) 1010101101(2) - 110011110(2);
б) 1010001111(2) -1001001110(2);
в) 1111100100,0111(2) -101110111,011(2);
г) 1437,24(8) - 473,4(8);
д) 24А,4(16) – В3,8(16).
3.
а) 101011(2) * 100111(2);
б) 1732,4(8) * 34,5(8);
в) 36,4 (16)* А,А(16).
Вариант №5
1.
а) 1100011010(2) + 11101100(2);
б) 10111010(2)+ 1010110100(2);
в) 1000110111,011(2) + 1110001111,001(2);
г) 1745,5(8) + 1473,2(8);
д) 24D,5(16) + 141,4(16).
2.
а) 1100101010(2) - 110110010(2);
б) 110110100(2) -110010100(2);
в) 1101111111,1(2) -1100111110,011(2);
г) 1431,26(8) - 1040,3(8);
д) 22С,6(16) – 54,2(16).
3.
а) 1001001(2) * 11001(2);
б) 245,04(8) * 112,2(8);
в) 4В,2 (16)* 3С,3(16).
Вариант №6
1.
а) 10000011101(2) + 1010000010(2);
б) 100000001(2)+ 1000101001(2);
в) 101111011,01(2) + 1000100,101(2);
г) 1532,14(8) + 730,16(8);
д) ВВ,4(16) + 2F0,6(16).
2.
а) 1000101110(2) - 1111111(2);
б) 1011101000(2) -1001000000(2);
в) 1000101001,1(2) -1111101,1(2);
г) 1265,2(8) - 610,2(8);
д) 409,D(16) – 270,4(16).
3.
а) 111010(2) * 1100000(2);
б) 1005,5(8) * 63,3(8);
в) 4А,3 (16)* F,6(16).
Вариант №7
1.
а) 1100110(2) + 1011000110(2);
б) 1000110(2)+ 1001101111(2);
в) 101001100,101(2) + 1001001100,01(2);
г) 275,2(8) + 724,2(8);
д) 165,6(16) + 3Е,В(16).
2.
а) 1011111111(2) - 100000011(2);