Проверка на статистическую значимость коэффициентов уравнения регрессии и корреляции.

Качество подбора функции регрессии можно оценить с помощью стандартных ошибок или оценок параметров регрессии. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной стандартного отклонения, т.е.:

t_b = b / S_b , t_a = a / S_a, t_R = R / S_R.

Стандартные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

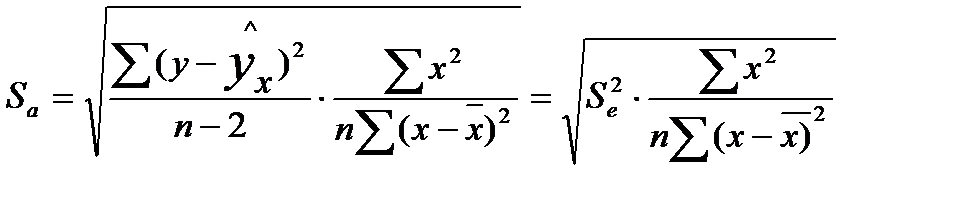
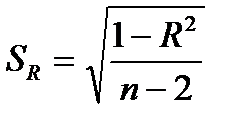
где 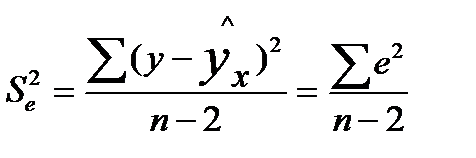- мера разброса зависимой переменной вокруг линии регрессии (необъясненная дисперсия) или 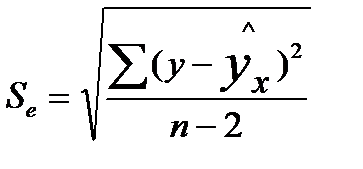- стандартная ошибка регрессии.

Сравнивая фактическое (расчетное) и критическое (табличное) значения t-статистики, т.е. t_факт и t_крит = t _n-1;α - отвергаем или не отвергаем гипотезу Н₀:

- если t_крит < t_факт, то Н₀ отклоняется, т.е. a, b и R не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора Х.

- если t_крит > t_факт, то Н₀ не отклоняется и признается случайная природа формирования a, b и R..

Фактическое значение t-критерия Стьюдента определяется как

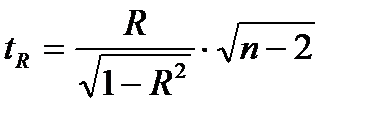
Данная формула свидетельствует, что в парной регрессии 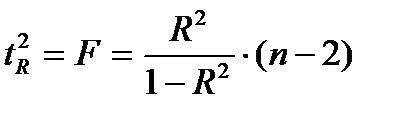. Кроме того 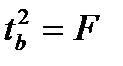. Следовательно,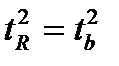

Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Формулы для расчета доверительных интервалов a, b имеют следующий вид:

a - t_крит S_a ≤ a ≤ a + t_крит S_a,

b + t_крит S_b ≤ b ≤ b + t_крит S_b.

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, т.к. он не может одновременно принимать и положительное, и отрицательное значения.

8.Проверка общего качества уравнения регрессии. Для оценки качества построенной модели используют коэффициент (индекс) детерминации - R², а также среднюю ошибку аппроксимации - А.

F-тест - оценивание качества уравнения регрессии – состоит в проверке гипотезы H₀ о статистической не значимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F -критерия Фишера. F_табл определяется из соотношения значения объясненной и остаточной дисперсии, рассчитанных на одну степень свободы:

где n - объем выборки (объем статистической информации).

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если F_табл < F_факт, то H₀ - гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность. Если F_табл > F_факт, то гипотеза H₀ не отклоняется и признаётся статистическая незначимость, ненадёжность уравнения регрессии.

9.Интервалы прогноза по линейному уравнению регрессии. В прогнозных расчетах по уравнению регрессии определяется предсказываемое (расчетное) у_прог значение как точечный прогноз при х_прог=х_к, т.е. путем подстановки в уравнение регрессии 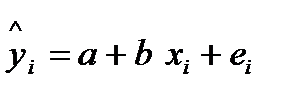соответствующего прогнозного значения x_прог. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки и соответственно интервальной оценкой прогнозного значения g_{прогноз.} Фактические значения у варьируют около среднего значения . Индивидуальные значения у могут отклоняться от на величину случайной ошибки e, дисперсия которой оценивается какостаточная дисперсии на одну степень свободы S². Поэтому ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку

S , но и случайную ошибку S_e.

Средняя стандартная ошибка прогноза S_{прогноз} вычисляется по формуле:

,

а доверительный интервал прогноза строится по формуле:

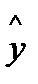_{прогноз} - t_крит S_{прогноз} ≤ g_{прогноз} ≤ _{прогноз} + t_крит S_{прогноз}

При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора.

10.Таблица дисперсионного анализа. Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной: å = å ( )² + å ( )²,

где 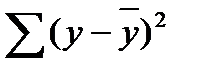- общая сумма квадратов отклонений;

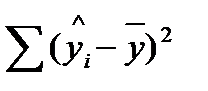- сумма квадратов отклонений, обусловленная регрессией («объясненная», «факторная»);

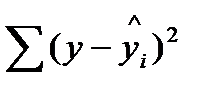- остаточная сумма квадратов отклонений (“необъясненная”).

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая		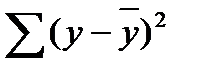n-1	-
Факторная		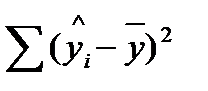m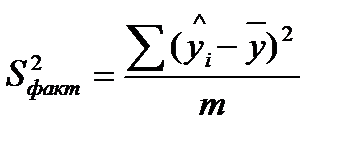
Остаточная		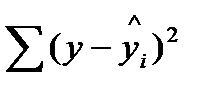n-m-1

Нелинейная регрессия

Нелинейная регрессия -частный случай регрессионного анализа, в котором рассматриваемая регрессионная модель есть функция, зависящая от параметров и от одной или нескольких свободных переменных. Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако в силу однообразия и сложности экономических процессов ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравнениями регрессии, безусловно, не даст положительного результата. Например, при рассмотрении спроса Y на некоторый товар от цены X данного товара в ряде случаев можно ограничиться линейным уравнением регрессии: Y=β₀+β₁X. Здесь β₁ характеризует абсолютное изменение Y (в среднем) при единичном изменении X. Если же мы хотим проанализировать эластичность спроса по цене, то приведенное уравнение не позволит это осуществить. В этом случае целесообразно рассмотреть так называемую логарифмическую модель

При анализе издержек Y от объема выпуска X наиболее обоснованной является полиноминальная (точнее, кубическая) модель При рассмотрении производственных функций линейная модель является нереалистичной. В этом случае обычно используются степенные модели. Например, широкую известность имеет производственная функция Кобба-Дугласа Y=AK^αL^β (здесь Y – объем выпуска; K и L – затраты капитала и труда соответственно; A, α и β – параметры модели).

Достаточно широко применяются в современном эконометрическом анализе и многие другие модели, в частности обратная и экспоненциальная модели.

Построение и анализ нелинейных моделей имеют свою специфику. Приведенные выше примеры и рассуждения дают основания более детально рассмотреть возможные нелинейные модели.