Расчет по прочности сечения, наклонного к продольной оси плиты

Расчет прочности наклонных сечений выполняется согласно п. 3.29…3.31 [4].

Поперечная сила Q = 33,81 кН.

q_l=q=12,14кН/м

Предварительно приопорные участки плиты заармируем в соответствии с конструктивными требованиями п. 5.27 [4]. Для этого с каждой стороны плиты устанавливаем по четыре каркаса длиной l /4 с поперечными стержнями Æ4Вр‑I, шаг которых s =10 см (по п. 5.27 [4] или
мм).

По [4, форм. 72] проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами:

Коэффициент, учитывающий влияние хомутов, j_{w 1} = 1 + 5 am_w £ 1,3,

Коэффициент поперечного армирования:

; A_sw = 0,5 см² (4Æ4 Bp-I);

j_{w 1} = 1 + 5 ´ 7,08 ´ 0,0013 = 1,05 < 1,3.

Коэффициент j_{b 1} = 1 – bg_b2R_b = 1 – 0,01 ´ 0,9 ´ 10,35 = 0,9, где b = 0,01 для тяжелого бетона.

Q = 25,3 кН < 0,3´1,05´0,9´0,9´11,5´37,7´19´100 = 210179 Н = 210,2 кН.

Следовательно, размеры поперечного сечения плиты достаточны.

Проверяем необходимость постановки расчетной поперечной арматуры из условия:

Коэффициент j_b3 = 0,6 для тяжелого бетона.

Проверяем условие (93) :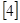

2,5 R_btbh₀ =2.5×0.81×377×190=145.1кН³Q=33,81кН т.е. условие выполняется.

Проверяем условие 93 (4), принимая упрощенно Q_b1=Q_b,min и с=2,5; h₀=2,5×0,19=0,475м.

Находим усилие обжатия от растянутой арматуры:

P=0,7 s_sp A_sp=0.7×745×471=245.6кН

Вычисляем:

тогда Q_b,min= кН

Q_b1 =Q_b,min=47,38кН

Так как Q=Q_max – ql×c=33,81 – 12,14×0,475=28,04кН, следовательно для прочности наклонных сечений по расчету арматуры не требуется. Поперечная арматура ставится по конструктивным требованиям.

Рисунок 2.4 Расчетное сечение плиты для расчетов по второй группе предельных состояний.

 

Рисунок 2.5 — Плита П-1

Расчет плиты по предельным состояниям второй группы

Согласно таблице 2 (2), круглопустотная плита эксплуатируется в закрытом помещении и армируется напрягаемой арматурой класса А-V диаметром 10мм и должна удовлетворять 3-й категории требований по трещиностойкости, то есть допускается непродолжительное раскрытие трещин шириной а_crc1=0,4мм, и продолжительное а_crc2=0,3мм. Прогиб плиты от действия постоянных и длительно действующих нагрузок не должен превышать fn=30,7мм (по таблице 19 (8)).

Определение геометрических характеристик сечения

Вычисляем геометрические характеристики сечения плиты:

Площадь приведенного сечения:

A_red=b_f¢h_f¢+bh_p+ b_f h_f+ A_sp=

=1460×38,9+458×143,1+1490×38+7,04×402=1817,84×10²мм²

S_red= b_f¢h_f¢(h-0.5 h_f¢)+bh_p(h_f+0.5h_p)+0.5 b_f h_f²+ A_spa=

=1460×38,9(220-0,5×38,9)+458×143,1(38+0,5×143,1)+0,5×1490×38²+7,04×

×24=1971,36×10⁴мм³

y₀= S_red/ A_red=1971,36×10⁴мм³/1817,84×10²мм²=108.5мм

 

y₀¢=h- y₀=220-108.5=111.5мм

Момент инерции:

I_red= b_f¢h_f¢³/12+ b_f¢h_f¢(y₀¢-0.5 h_f¢)²+bh_p³/12+bh_p(y₀- h_f -0.5h_p)²+ b_f h_f³/12+ b_f h_f×

×(y₀-0.5 h_f)²+ A_sp(y₀-a)²

I_red=1460×38,9³/12+1460×38,9(111,5-0,5×38,9)²+458×143,1³/12+458×143,1×

×(108,5-38-0,5×143,1)²+1490×38³/12+1490×38(108,5-0,5×38)²+7,04×402×

×(108,5-24)²=1080,86×10⁶мм⁴

Момент сопротивления:

W = I_red/ y₀=1080,86×10⁶/108.5=996.18×10⁴мм³

W = I_red/ y₀¢=1080,86×10⁶/111.5=969.38×10⁴мм³

По таблице 38 (5) находим коэффициент =1,5

W = W =1,5×996.18×10⁴=1494,27×10⁴мм³

W = W =1,5×969.38×10⁴=969,38×10⁴мм³

Определение потерь

Первые потери определяем по таблице 5 (2) поз.1-6.

Коэффициент точности натяжения арматуры _p=1. Потери от релаксации напряжений в арматуре при электротермическом способе натяжения:

_×_sp=0.03×745=22,35 МПа

Потери от температурного перепада между натянутой арматурой и упорами: ₂=1,25×65=81,25МПа

Остальные потери ₃, ₄, ₅ – отсутствуют.

Таким образом усилие обжатия P₁ с учетом потерь по поз. 1-5 таблицы 5 (2) равно: P₁=A_s×(_sp-₁-₂)=471×(745-22,35-81,25)=257,84кH

Точка приложения усилия P₁ совпадает с центром тяжести сечения напрягаемой арматуры, по этому: e_op=y₀-а=108,5-30 = 78,5мм

Определяем потери от быстро натекающей ползучести бетона, для чего вычисляем напряжение в бетоне в середине пролета от действия силы P₁ и изгибающего момента М_w от собственной массы плиты.

Нагрузка от собственной массы плиты равна q_w=3,0×1,5=4,5кН/м, тогда

М_w= q_wl₀/8=4,5×5,57²/8=17,45кНм

Напряжение на уровне растянутой арматуры _bp (т.е. при y= e_op=78.5) будет равно:

(257,84×10³)/(1817,84×10²)+(257,84×10³×78,5-17,45×

×10⁶)×78,5/(1080,86×10⁶)=1,76МПа

Напряжение на уровне крайнего сжатого волокна _bp¢ (т.е. при у=h-у₀=220-

- 108,5=111,5мм)

_bp¢=(257,84×10³)/(1817,84×10²)-(257,84×10³×78,5-17,45×10⁶)×111,5/(1080,86×

×10⁶)=0,97МПа

Назначаем придаточную прочность бетона R_bp=20МПа (R =15МПа, R 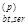=1,4МПа) удовлетворяющую требованиям п.2.6(2).

Потери от быстро натекающей ползучести бетона будут равны:

- на уровне растянутой арматуры

=0,25+0,025 R_bp=0,25+0,025×20=0,75≤0,8

Поскольку _bp/ R_bp=1,76/20=0,088£ =0,75, то ₆=40×0,85(_bp/ R_bp)=40×0,85×

×(1,76/20)=2,99МПа (коэффициент 0,85 – учитывает тепловую обработку при твердении бетона)

– на уровне крайнего сжатого волокна ₆¢=40×0,85(0,97/20)=1,65МПа

Первые потери составят:

_loc1=₁+₂+₆=22.35+81.25+2.99+106.6МПа

Тогда усилие обжатия с учетом первых потерь

P₁= А_sp×(_sp-_los1)=471(745-106.6)=256.64кН

Определяем максимальное сжимающее усилие в бетоне от действия силы P₁, без учета собственной массы, принимаем у=у₀=108,5мм,

 

 

Поскольку _bp/R_bp=3,59/20=0,18≤0,95, требования п.1.29(2) удовлетворяются.

Определяем вторые потери предварительного напряжения по позиции 8 и 9 таблицы 5 (2).

Потери от усадки тяжелого бетона: ₈–₈¢=35МПа

Напряжения от действия силы P₁ и изгибающего момента Мw будут равны:

_bp=

 

_bp¢=

 

Так как _bp/R_bp£0,75 и _bp¢/R_bp£0,75, то ₉=150 (_bp/R_bp)=150×0,85(1,74/20)=11,09МПа

₉¢=150×0,85(0,97/20)=6,18МПа

Тогда вторые потери будут равны:

_loc2=₈+₉=35+11.09=46.09МПа

Суммарные потери будут составлять:

_loc=_loc1+_loc2=106,6+46,09=152,7МПа³100 МПа, по этому, согласно п. 1.25 (2) потери не увеличиваем.

Усилие обжатия с учетом суммарных потерь будет равно:

P₂= А_sp×(_sp-_los)=471(745-152,7)=238,1кН

Проверку образования трещин в плите выполняем по формулам п. 4.5 (2) для выяснения необходимости расчета по ширине раскрытия трещин и выявления случая расчета по деформациям.

При действии внешних нагрузок в стадии эксплуатации максимальное напряжение в сжатом бетоне равно:

 

 

Тогда =1,6-_b/ R =1,6-3,47/15=1,37³1, принимаем =1, а r_sup= ×

×(W 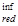/ А_red)=1(996.18×10⁴/1817.84×10²)=54.8мм

Так как при действии усилия обжатия P₁ в стадии изготовления минимальное напряжение в бетоне (в верхней зоне) равно:

 

 

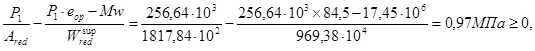
то есть будет сжимающим, следовательно верхние начальные трещины не образуются.

Согласно п. 4.5(2) принимаем:

M_r=M_tot=41.07кНм

M_rp=P₂(e_op+r_sup)=238.1×10³(84.5+54.8)=33.17кНм

M_crc= R W + M_r=1,4×1494,27×10⁴+33,17×10⁶=54,1кНм

Так как M_crc=54,1кНм³ M_r=41,07кНм, то трещины в нижней зоне не образуются, то есть не требуется расчет ширины раскрытия трещин.

Расчет прогиба плиты выполняем согласно пп. 4.24, 4.25(2) при условии отсутствия трещин в растянутой зоне бетона.

Находим кривизну от действия постоянной и длительной нагрузок (М=М_l=37,32кНм, _b1=0.85, _b2=2)

 

Прогиб плиты без учета выгиба от усадки бетона при предварительном обжатии будет равен:

 

Это значит, что прогиб допустимый.