Исследование деформации балки при чистом изгибе проводится на экспериментальной установке типа СМ−47А.
| 7 6 5 4 3 8 2 1 |
Рисунок 7.2 - Схема установки СМ-47А
Рис. 5.1. Схема установки СМ−47А
Установка состоит из станины 1, на которой закреплена балка 5, нагружаемая одинаковыми изгибающими моментами, возникающими на роликах 4 от действия грузов 3.
Под действием нагрузки балка изгибается и перемещает по направляющей 6 измеритель прогиба 7, упирающийся в ее середину. До нагружения верхняя грань измерителя устанавливается на одном уровне с верхним срезом направляющей. Таким образом, после нагружения измеренный отрезок измерителя 7 над верхним срезом направляющей будет равен прогибу середины балка. Для проверки положения, что изогнутая ось балки является дугой окружности, служит стрелка 2, вращающаяся вокруг оси 8. Так, после вычисления экспериментального значения 
, опора стрелки 2 при нагруженной установке устанавливается на расстоянии Rэкс от середины нагруженной балки или от оси вращения одного из роликов 4. Отклонение стрелки в любую сторону является доказательством, что радиус кривизны нагруженной балки во всех ее точках постоянен, то есть изогнутая ось балки представляет собой дугу окружности.
Геометрические размеры балки, необходимые для обработки результатов испытания, измеряются при помощи штангенциркуля или микрометра. Балка, изготовленная из пружинной стали, представляет собой гибкую линейку, для которой закон Гука справедлив при значительных деформациях. Установка рассчитана на применение грузов весом не более 1,0 кг.
Экспериментальное значение радиуса кривизны балки определяется косвенным путем из геометрических соотношений (рис.5.2) и выражается через прогиб середины балки. Величина прогиба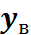 
в середине пролета балки определяется измерением в ходе проведения испытаний.
m m
А В С
R R
О
▪ O
|
Рис.5.2. Расчетная схема экспериментальной установки в нагруженном состоянии.
Из 
имеем:
(5.1)
После преобразований получаем зависимость радиуса кривизны балки от экспериментально полученного прогиба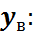 
,(5.2)
где ℓ – длина балки, мм;
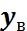– прогиб в середине балки, мм.
Сведения из теории:
При нагружении балки на двух опорах двумя противоположно направленными одинаковыми моментами М, приложенными в сечениях над опорами балки, возникает деформация чистого изгиба, при которой в поперечных сечениях балки действует только один внутренний силовой фактор - изгибающий момент 
. При этом величина его во всех сечениях балки остается постоянной.
Из выражения закона Гука при изгибе кривизна изогнутой оси в точках балки при этом имеет значение:
, (5.3)
где К – кривизна продольной оси балки;
ρ – радиус кривизны, мм;
– изгибающий момент, Н∙мм;
E – модуль продольной упругости (Е = 2∙ 
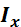– момент инерции поперечного сечения балки относительно нейтральной оси x, мм4.
Для нашего случая нагружения 
Это значит, что изогнутая ось балки будет иметь форму окружности радиуса R, величина которого определяется по формуле:
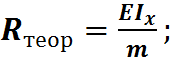(5.4)
.
Величина приложенных к балке моментов m определяется по формуле:
(5.5)
где F −величина приложенной к роликам нагрузки, H;
D − диаметр роликов, установленных на опорах балки, D=70 мм.