В ненагруженной установке верхний срез направляющей 6 устанавливается на одном уровне с верхним срезом ограничителя 7. На каждую грузовую платформу устанавливают грузы одинаковой массы. После этого часть ограничителя, расположенную выше верхнего среза направляющей 6 (прогиб середины нагруженной балки), измеряют штангенциркулем. Определяют по формуле (5.2) экспериментальную величину радиуса кривизны.
Затем устанавливают опору 8 на расстоянии от середины нагруженной балки (или от оси одного из роликов 4), равном величине полученного радиуса кривизны.
Поворотом стрелки вокруг оси 8 убеждаются, что при повороте стрелки 2 в любую сторону конец стрелки находится в постоянном свободном контакте с деформированной балкой, то есть радиус кривизны балки во всех сечениях одинаков. Опыт повторяют при различных величинах нагрузки.
Таблица 5.1
Таблица экспериментальных данных
| Нагрузка F, Н | Размеры сечений
b  h, мм
| Длина балки ℓ, мм | Ix, мм4 | m, Н∙мм | Прогиб yВ, мм | Радиус кривизны стержня, мм | Погреш- ность, % | |
|
| |||||||
Обработка результатов испытаний.
Подставляя полученную опытным путем величину прогиба середины балки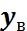 
в формулу (5.2), определяют экспериментальное значение радиуса кривизны 
. По формуле (5.4) определяют теоретическое значение радиуса кривизны балки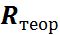 
.
Сравнивают между собой экспериментальное и теоретическое значение радиуса кривизны балки и определяют относительную погрешность по формуле:
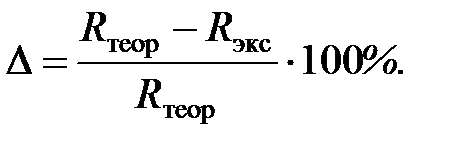(5.4)
Выводы.
В выводах по работе необходимо привести результаты сравнения полученных экспериментально величин радиуса кривизны балки с теоретическими значениями, а также сформулировать доводы, подтверждающие теорию чистого изгиба.
Контрольные вопросы
- От каких внешних нагрузок возникает чистый изгиб?
- Какие внутренние силовые факторы возникают при чистом изгибе?
- В чем заключается закон Гука при изгибе?
- В каком случае изогнутая ось балки представляет собой часть окружности?
- Как экспериментально определяется радиус кривизны балки?
Литература: [1, 2, 3, 4,5,6].
ЛАБОРАТОРНАЯ РАБОТА №6
«Испытание стержня на устойчивость»
(2 часа)
Цель работы:
1.Исследовать явление потери устойчивости упругого стержня при сжатии.
2. Определить величину критической силы экспериментальным методом и сравнить полученные результаты с теоретическими.
Сведения из теории:
Прямолинейный центрально сжатый стержень при определенных условиях может оказаться в состоянии, когда смещение любой точки балки от прямолинейной продольной оси приводит к возникновению в сечениях балки дополнительного изгибающего момента, приводящего к возникновению продольного изгиба. В этом случае, при некоторой зависящей от параметров данного стержня величине приложенной внешней нагрузки, происходит лавинообразное увеличение изгибных деформаций без увеличения внешней нагрузки вплоть до разрушения стержня. Это состояние стержня носит название потери устойчивости и является критическим состоянием сжатого стержня. Минимальная величина силы, при которой стержень теряет устойчивость, называется критической силой, а величина возникающего при этом напряжения – критическим напряжением.
При значении критического напряжении, не превышающем предела пропорциональности материала, теоретическая формула для определения величины критической силы для гибких стержней (формула Эйлера) имеет вид:
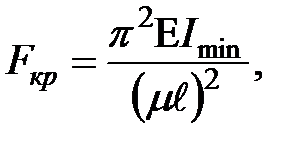(6.1)
где m - коэффициент приведения длины (учитывает способ закрепления концов стержня);
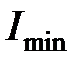− минимальный осевой момент инерции сечения стержня (наименьший из главных центральных моментов инерции сечения), мм4;
Е − модуль продольной упругости материала, МПа;
ℓ − длина стержня, мм.
Применимость формулы Эйлера определяется величиной гибкости стержня:
, (6.2)
где 
− минимальный радиус инерции сечения, мм;
А − площадь поперечного сечения стержня, мм2.
Так, достоверные результаты применения формулы Эйлера получаются, если гибкость стержня больше некоторой величины, называемой предельной гибкостью r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
(такие стержни называют стержнями большой гибкости). Эта гибкость определяется выражением:
, (6.3)
где 
− предел пропорциональности материала, МПа.
Для различных материалов предельные значения гибкости равны: для малоуглеродистой стали 
, для дюралюминия 
, древесины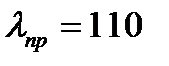 
и т.д.
При значениях гибкости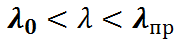 
, (стержни средней гибкости) формула 6.1 не дает достоверных результатов, так как критическое напряжение в этом случае превышают предел пропорциональности и на величину критической силы сильно влияют дополнительно появляющиеся пластические деформации. В таких случаях используется эмпирическая формула Ф.С. Ясинского.
Формула Ясинского для определения критической силы имеет вид:
(6.4)
где a и b −эмпирические коэффициенты (для стали марки Ст. 3 при 60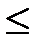 
имеют значения a =310 МПа, b =1,14 МПа
При гибкости стержня 
расчеты на устойчивость не проводятся, так как стержни такой гибкости разрушаются от напряжений простого одноосного сжатия раньше, чем потеряют устойчивость. Эти стержни малой гибкости не считаются гибкими и относятся к категории стержней большой жесткости.
Отношение критической силы к ее допускаемой величине называется коэффициентом запаса устойчивости 
. (6.5)
Следует отметить, что расчет на устойчивость в подавляющем числе проектировочных расчетов носит проверочный характер.
Величина коэффициента при этом 
должна обеспечивать гарантированное отсутствие потери устойчивости нагруженного заданными нагрузками сжатого стержня. Для стальных стержней его оптимальная (нормативная) величина принимается в пределах: для общемашиностроительных материалов - от 1,5 до 2,5, для деревянных конструкций – от 3,5 до 5,0.
Допускаемая нагрузка 
в расчетах на устойчивость должна выбираться из условия:
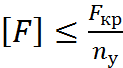; (6.6)
Оборудование и материалы:
Экспериментально величину критической силы для прямолинейного консольного стержня, защемленного одним концом, определяют на специальной установке ТМ-3 (рис. 6.1).
Установка состоит из основания 1 с установленной на нем пятой 2, обеспечивающей жесткое защемление стержня испытуемого образца 3. На другом (свободном) конце стержня установлен стакан 4, который создает осевую сжимающую нагрузку на консольно закрепленный вертикальный стержень 3, за счет насыпания в стакан свинцовой дроби.
Рис. 6.1 Схема экспериментальной установки.