Описание входных и выходных данных подпрограммы в терминах фактических параметров

Перейдем теперь к решению второй задачи межпроцедурного анализа - описанию входных и выходных данных подпрограммы в терминах фактических параметров. Описываемый здесь метод опирается на [9,16] и требует, чтобы входные и выходные данные подпрограммы уже были описаны в виде системы линейных неравенств.

Пусть в программе есть две подпрограммы P и Q, такие, что:

SUBROUTINE P(...)

DIMENSION A_p(lp₁:up₁,...,lp_p:up_p)

...

CALL Q(...,A_p(op₁,...,op_p),...)

...

END

SUBROUTINE Q(...,A_q,...)

DIMENSION A_q(lq₁:uq₁,...,lq_q:uq_q)

...

END

Пусть элементы массива A_q, представляющие часть входных и выходных данных подпрограммы Q, представлены в виде области W_q, описанной с помощью набора линейных равенств и неравенств. Требуется пересчитать эту область в терминах вырезки из соответствующего фактического параметра-массива A_p.

Запишем условие Г_pq того, что два элемента массивов A_p(y₁,..., y_p) и A_q(j₁,..., j_q) ссылаются на одну и ту же область памяти:

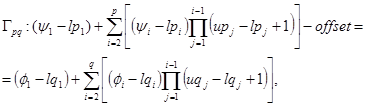
где .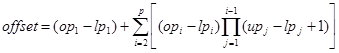

Тогда пересечение трех областей W=W_qÇГ_pqÇ{lp_i£y_i£up_i, i =1,p} неявно задает область W_p массива A_p, соответствующую области W_q массива A_q. Для получения явного описания W_p необходимо получить проекцию (p+q)-мерной области W на p-мерное подпространство, соответствующее массиву A_p. Это можно сделать с помощью исключений Фурье-Моцкина [12,13], если равенство Г_pq линейно. Определение условий его линейности рассматривается дальше.

Если равенство Г_pq нелинейно, то при некоторых условиях можно получить более простое условие. Если массивы A_p и A_q имеют одинаковое число элементов в первых (d-1) размерностях (то есть {up_i - lp_i = uq_i - lq_i, 1 £ i £ d-1}), и {op_i=lp_i, 1 £ i £ d-1}, то добавим в описание области W равенства {y_i - lp_i=j_i - lq_i, 1 £ i £ d-1} и составим частичное уравнение ранга d:

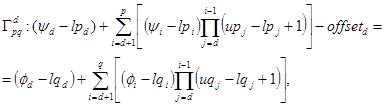
где .

Это уравнение проще, чем Г_pq, и в реальных случаях может оказаться линейным, в то время как полное уравнение таковым не является. Если количество размерностей с одинаковым числом элементов равно q, но меньше p, то в описание области W вместо условия Г^d_pq нужно добавить равенства {y_i=op_i, | i=q+1,p }.

Для того, чтобы получить проекцию (p+q)-мерной области W на p-мерное пространство, необходимо исключить переменные, введенные для описания W_q, из всех равенств и неравенств. Это можно сделать методом Фурье-Моцкина [12,13], если все ограничения, содержащие эти переменные, линейны. Так как в описание W_q входят только линейные ограничения, нелинейность по данным переменным может возникнуть только в равенстве Г_pq (Г^d_pq). Кроме того, для проведения дальнейшего анализа программы важно, чтобы все получающиеся ограничения также были линейными. Поэтому нужно выделить условия на внешние переменные, при которых Г_pq (Г^d_pq) будет линейным по всем переменным.

Для этого берем равенство Г_pq (Г^d_pq), приводим в нем подобные, после чего приравниваем к нулю все нелинейные части. Если из получившихся равенств можно выразить переменные, введенные для описания W_q, через внешние переменные, и подстановка этих выражений в ограничения вместо переменных не входит в противоречие с заданными ограничениями на внешние переменные, то добавим к равенству Г_pq (Г^d_pq) с зануленными нелинейными частями ограничения {lp_i£y_i£up_i|1£i£p} и {lq_i£j_i£uq_i|1£i£q}. После этого исключаем из получившихся линейных ограничений все переменные, кроме внешних, и получаем искомые ограничения на внешние переменные.