Определение 3. 6.
Число, равное произведению длин двух векторов на косинус угла между ними называется скалярным произведением этих векторов. Для векторов  и
и 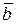 их скалярное произведение обозначается (
их скалярное произведение обозначается ( ,
,  ), или
), или  .
.  .
.
Таким образом, по определению
 .
.  = |
= |  |.|
|.|  | cos
| cos  .
.
Скалярное произведение обладает свойствами:
1.  .
.  =
=  .
.  ;
;
2.  . (
. ( + `с) =
+ `с) =  .
.  +
+ 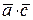 ;
;
3.  .
.  = |
= |  |2 =
|2 =  2 – скалярный квадрат; отсюда
2 – скалярный квадрат; отсюда  ;
;
4. l  .
.  = (l
= (l  ).
).  =
=  . (l
. (l  );
);
5.  .
.  = 0 тогда и только тогда, когда хотя бы один из векторов нулевой, либо когда векторы
= 0 тогда и только тогда, когда хотя бы один из векторов нулевой, либо когда векторы  и
и  ортогональны;
ортогональны;
6.  . Пользуясь этим свойством, получим
. Пользуясь этим свойством, получим
 .
.
Заметим, что для ортонормированного базиса {` i,` j,` k } пространства V3 справедливы следующие соотношения
 ,
,
 .
.
Пусть в ДПСК, порожденной репером [O,` i,` j,` k ], заданы два вектора
 и
и  .
.
Используя перечисленные свойства скалярного произведения, получим для этих векторов:
 .
.  =
=  .
.  =
= 
+  =
=
=  .
.
Таким образом, если векторы заданы своими координатами в ДПСК, то их скалярное произведение равно сумме произведений соответствующих координат этих векторов:
 .
.  =
=  .
.
Пользуясь этим правилом, можно записать в координатной форме
|  | = (
| = ( .
.  ) =
) =  ,
,
 =
=  .
.
Учитывая эти формулы и следствие из свойства 6, находим:


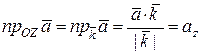 ,
,
т.е. в ДПСК координаты вектора равны его проекциям на соответствующие оси координат.
Для направляющих косинусов вектора ` а имеем
 ,
,
 ,
,
 .
.
Рассмотрим орт `а о вектора ` а. Учитывая координаты вектора ` а,находим
`а о =  .
.
Следовательно, направляющие косинусы вектора равны координатам его орта и наоборот, т.е. можно записать `а о = (cosa, cosb, cosg).
Определение 3.7.
Упорядоченная тройка векторов ` а,` b,` c, совмещенных началами, называется правой тройкой, если из конца третьего вектора` с кратчайший поворот от первого вектора` а ко второму вектору` b виден осуществляющимся против часовой стрелки.
В противном случае тройка векторов называется левой. На рис.7а изображена правая тройка векторов, а на рис.7б – левая.
 | |||||||
 | |||||||
 | |||||||
| |||||||
ДПСК, которой мы договорились пользоваться, строится на основе правой тройки (` i,` j,` k).
Определение 3.8.
Векторным произведением векторов ` а и ` b называется вектор` v, удовлетворяющий свойствам:
а) |  | = |
| = |  |.|
|.|  |. sin
|. sin  ,
,
б) вектор` v перпендикулярен плоскости, в которой лежат векторы  и
и  ;
;
в) векторы  ,
,  ,` v, взятые в указанном порядке, образуют правую тройку
,` v, взятые в указанном порядке, образуют правую тройку
Векторное произведение обозначается  ´
´  или [
или [  ,
,  ]. Векторное произведение обладает свойствами:
]. Векторное произведение обладает свойствами:
1)  ,
,
2)  ,
,
3)  = l(
= l( ) =
) =  ,
,
4)  =`0 (
=`0 ( ¹`0,
¹`0,  ¹`0) тогда и только тогда, когда векторы
¹`0) тогда и только тогда, когда векторы  и
и  коллинеарны. В частности,
коллинеарны. В частности,  .
.
Для базисных векторов ` i,` j,` k имеют место соотношения:


 .
.
Пусть векторы заданы своими координатами:
 и
и  .
.
Используя перечисленные свойства, получим
 =
=  ´
´  =
= 
+  =
=
= 
= 
=  .
.
Таким образом, через координаты перемножаемых векторов ` a = (ax, ay, az) и ` b = (bx, by, bz) векторное произведение может быть записано в виде символического определителя
 .
.
или в виде координатной строки
 ´
´  =
=  .
.
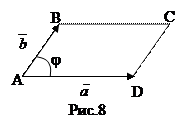 Рассмотрим параллелограмм ABCD, построенный на векторах` а и` b как на сторонах (рис. 8). Площадь этого параллелограмма равна
Рассмотрим параллелограмм ABCD, построенный на векторах` а и` b как на сторонах (рис. 8). Площадь этого параллелограмма равна
Sпар. = |AB|.|AD|.sinj = |  |.|
|.|  |. sinj = |
|. sinj = |  ´
´  |.
|.
Таким образом, с геометрической точки зрения, модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
Определение 3.9.
С мешанным произведением векторов` а,` b,` с называется скалярное произведение вектора  ´
´  на вектор ` с. Обозначается смешанное произведение
на вектор ` с. Обозначается смешанное произведение  .
.  .
.  или
или 

 .
.
Таким образом, по определению, смешанное произведение трех векторов – это число, равное
 .
.  .
.  = (
= ( ´
´  , ` с).
, ` с).
Свойства смешанного произведения:
1)  .
.  .
.  =
=  .
.  .
.  =
=  .
.  .
.  , т.е. при циклической перестановке множителей смешанное произведение не меняется;
, т.е. при циклической перестановке множителей смешанное произведение не меняется;
2)  .
.  .
.  = –
= –  .
.  .
.  = –
= –  .
.  .
.  = –
= –  .
.  .
.  , т.е. смешанное произведение меняет знак при перестановке соседних множителей;
, т.е. смешанное произведение меняет знак при перестановке соседних множителей;
3)  .
.  .
.  = 0 (
= 0 ( ¹`0,
¹`0,  ¹`0,
¹`0,  ¹`0) тогда и только тогда, когда векторы ` a,` b,` c компланарны.
¹`0) тогда и только тогда, когда векторы ` a,` b,` c компланарны.
Если векторы ` a,` b,` c заданы своими координатами:
` a = (аx, ay, az), ` b = (bx, by, bz), ` с = (сx, сy, сz),
то, используя координатную форму скалярного и векторного произведений, получим
 .
.  .
.  = (
= ( ´
´  , ` с) =
, ` с) =  . (сx, сy, сz) =
. (сx, сy, сz) =
= 
Следовательно, в координатной форме смешанное произведение имеет вид
 .
.  .
.  =
=  .
.
 Рассмотрим геометрическую интерпретацию смешанного произведения. Построим на векторах ` а,` b,` с как на ребрах параллелепипед (рис.9).
Рассмотрим геометрическую интерпретацию смешанного произведения. Построим на векторах ` а,` b,` с как на ребрах параллелепипед (рис.9).
Объем этого параллелепипеда равен V = Sосн.. Н. Но Sосн = |  ´
´  |,а высота Н равна Н =
|,а высота Н равна Н =  . Тогда
. Тогда
V =  = |(
= |( ´
´  , ` с)| = = |
, ` с)| = = |  .
.  .
.  |.
|.
Таким образом, если векторы` а, ` b, ` с некомпланарные, то объем V параллелепипеда, построенного на этих векторах, равен
V = |` a. ` b. ` c |,
то есть абсолютной величине смешанного произведения этих векторов.
Наряду со смешанным произведением трех векторов, можно рассмотреть и произведение вида  ´(
´( ´` с) – такое произведение называется двойным векторным произведением.
´` с) – такое произведение называется двойным векторным произведением.
Двойное векторное произведение обладает свойством, которое связывает векторное произведение со скалярным произведением и произведением вектора на число:
 ´(
´( ´` с) = (
´` с) = ( .
.  )
)  – (
– ( .
.  )
)  .
.