Рассмотрим задачу о теплообмене с полубесконечным изоливарованным с боковой поверхности стержнем, на поверхность которого падает поток  . В результате взаимодействия потока
. В результате взаимодействия потока  с поверхностью тела происходит повышение температуры поверхности
с поверхностью тела происходит повышение температуры поверхности  , и начальная разность температур среды и тела
, и начальная разность температур среды и тела  переходит в разность
переходит в разность  , а тепловой поток, идущий внутрь тела запишется как:
, а тепловой поток, идущий внутрь тела запишется как:
 (11)
(11)
Выражение (11) определяет тепловой поток, записанный в форме Ньютона-Рихмана. При этом начальный тепловой поток при  будем и дальше считать падающим
будем и дальше считать падающим  . В выражении (11) величина
. В выражении (11) величина  называется коэффициентом теплоотдачи от среды к телу, коэффициент теплоотдачи определяется в основном физическими свойствами среды и интенсивностью динамического (конвективного) взаимодействия между средой и повехрностью. В результате на границе раздела будет выполняться соотношение
называется коэффициентом теплоотдачи от среды к телу, коэффициент теплоотдачи определяется в основном физическими свойствами среды и интенсивностью динамического (конвективного) взаимодействия между средой и повехрностью. В результате на границе раздела будет выполняться соотношение
 (12).
(12).
Выражение (12) отражает тот факт, что первоначально падающий тепловой поток на поверхность тела  со временем уменьшается на величину
со временем уменьшается на величину 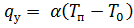 , а поток qВ идет внутрь тепла и нагревает его.
, а поток qВ идет внутрь тепла и нагревает его.
Граничное условие на поверхности тела для потока  имеет вид:
имеет вид:
 , x=0
, x=0

|

|
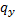
|
| Теплоизоляция с боков |
| Х |

|

|
В результате задача сводится к решению уравнения теплопроводности с граничными условиями третьего рода:
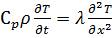 0≤х<∞ (14)
0≤х<∞ (14)


Условия на бесконечности  , x ∞
, x ∞
Решение поставленной задачи имеет вид [1]:
 (15)
(15)
Здесь
 (16)
(16)
В дальнейшем мы будем интересоваться преимущественно температурой и плотностью теплового потока на поверхности х=0. Для этого случая:
 , (17)
, (17)
где 
Функция erfx называется интегралом ошибок и ее значение берется в таблицах [2]

erf(o)=0, erf(∞) = 1
Из физических соображений ясно,что при t  , то есть произведение
, то есть произведение 
выражением (17) пользоватся затруднительно. При больших значениях  произведение
произведение  можно представить как: [2]
можно представить как: [2]

Cледовательно, решение (17) при больших значениях  можно записать:
можно записать:

При  > 8 будем считать величину в квадратных скобках равной 1 и, тогда
> 8 будем считать величину в квадратных скобках равной 1 и, тогда

Из этого выражения легко получить
 (18)
(18)
А если вспомнить, что тепловой поток, идущий внутрь тела  , то получим для потока внутрь:
, то получим для потока внутрь:
 (19)
(19)
Для 

Но если вспомнить, что величина  есть ничто иное как приближенное значение величины
есть ничто иное как приближенное значение величины  при
при  , то становится очевидным, что для любых значений
, то становится очевидным, что для любых значений 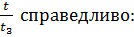

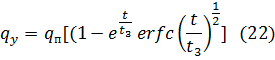
Произведение exp и erfc считать затруднительно, поэтому как и в случае  подыщем более удобные приближенные значения при
подыщем более удобные приближенные значения при 
Для малых значений  произведение разлагается по степеням
произведение разлагается по степеням  и получаются результаты:
и получаются результаты:
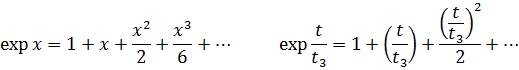
 ) + …, а следовательно
) + …, а следовательно
 0<t/t3<0.5 (23)
0<t/t3<0.5 (23)
 0.5<t/t3<25 (24)
0.5<t/t3<25 (24)
 t/t3≥25 (25)
t/t3≥25 (25)
Выражения (23)-(25) пригодны для определения температуры поверхности 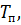 так как
так как  .
.
Коэффициент теплоотдачи определяется из условий задачи. Тепловой поток, идущий в конструкцию, можно определить из уловия:
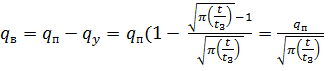 t/t3>25 (26)
t/t3>25 (26)
 , 0.5<t/t3<25 (27)
, 0.5<t/t3<25 (27)
 , 0<t/t3<0.5 (28)
, 0<t/t3<0.5 (28)
В выражении (26) условие  , заменим более точным
, заменим более точным  . Выражения (23)-(28) применяют для термически толстых тел. Термически толстым телом считается тело толщиной 𝝳 в течение времени t<
. Выражения (23)-(28) применяют для термически толстых тел. Термически толстым телом считается тело толщиной 𝝳 в течение времени t<  или Fo<0,5. В течение этого времени тепловое возмущение на обогреваемой поверхности x=0 не получит сигнала от условий на границе х =
или Fo<0,5. В течение этого времени тепловое возмущение на обогреваемой поверхности x=0 не получит сигнала от условий на границе х =  , то есть как будто
, то есть как будто 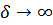 .
.
Пример. 1) Рассмотреть изменение температуры поверхности бетонной стены. Стена имеет следующие параметры: 𝝳=30 см,  . На стену падает тепловой поток
. На стену падает тепловой поток 
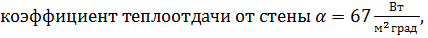 начальная температура стены Т0=20
начальная температура стены Т0=20 
1) Определяется время, в течение которого стена является термически толстым телом:

2) Характерное время изменения температуры поверхности стены:
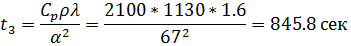
3) Предельная температура, до которой может нагреться поверхность стены, определяется из условия, что внутрь стены тепло не поступает  . Следовательно:
. Следовательно: 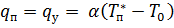
Предельная температура  равна:
равна:

Температура поверхности стены, в момент соответсвующий  когда кончается выполнение условия, что конструкция является термически толстым телом, вычисляется из выражения (25) при t=6.67*104 сек
когда кончается выполнение условия, что конструкция является термически толстым телом, вычисляется из выражения (25) при t=6.67*104 сек
 :
:
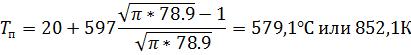
Температура, соотвествующая времени t/t3=25:

t/t3=12.5 по выражнию (24):




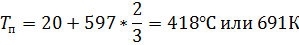


Далее расчет ведется по соотношению (23)









Термически тонкое тело.
Рассмотрим задачу о нагревании (об охлаждении) плоской пластины в следующей постановке (рис.4)

|

|

|
Пластина имеет толщину 𝝳, свойства материала пластины 
|
| x |
| Рис. 4 |
| Рис.4 |
Уравнение теплопроводности:
 , Начальное условие , Начальное условие  Граничное условие
Граничное условие  
|
Проинтегрируем по Х уравнение теплопроводности от 0 до 𝝳. Введем понятие средней по толщине температуры пластины:
 =
= 
В результате получим:
 (29)
(29)
То есть уравнение (29) есть обыкновенное дифференциальное уравнение для определения средней по толщине температуры пластины в разные моменты времени, однако необходимо найти связь между средней температурой и температурой поверхности.
Перепишем последнее уравнение в виде:

Величина  является характерным масштабом времени прогрева пластины по толщине. То есть определяет темп изменения средней температуры пластины. Сравним характерное время t1 и t2 и получаем:
является характерным масштабом времени прогрева пластины по толщине. То есть определяет темп изменения средней температуры пластины. Сравним характерное время t1 и t2 и получаем:

Bi – число Био показывает как быстро выравнивается температура пластины по сравнению с ее прогревом как целого. И поскольку t1 характеризует время выравнивания температуры по толщине, а t2 время прогрева как целого, то при Bi  выравнивание температуры происходит очень быстро, и мы имеем по существу пластину с однородной температурой по толщине.
выравнивание температуры происходит очень быстро, и мы имеем по существу пластину с однородной температурой по толщине.
Таким образом, при малых значениях числа Био можно считать, что температура пластины по толщине одинаковое и в уравнениях (29-29а) можно положить  . В этом случае уравнение (29а) перепишется в виде:
. В этом случае уравнение (29а) перепишется в виде:
 .
.
Если температуру выразить в величинах начальной температуры Т0, то есть  , а время в величинах t2, то есть
, а время в величинах t2, то есть  , то уравнение (31) примет безразмерный вид:
, то уравнение (31) примет безразмерный вид:
 (33)
(33)
С начальным условием  = 1. Решение этого уравнения при Тс= const имеет вид:
= 1. Решение этого уравнения при Тс= const имеет вид:
 (33)
(33)
 (34)
(34)
или в размерном виде:
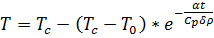 (34а).
(34а).
Полученное решение справедливо для случая Тс=const. Если температура среды меняется, то решение несколько усложняется.
Итак, уравнение для температуры термически тонкой пластины имеет вид:

Температура среды зависит от времени. Решение в этом случае имеет вид:
 (35)
(35)
Константа С определяется из начальных условий. Для практических расчетов будем считать, что при Bi≤0.1 тело можно считать термически тонким. Для термически тонкого тела требование теплоизоляции при x=  необязательно, и теплообмен может осуществляться с двух сторон. Приведем примеры определения температуры термически тонкого тела.
необязательно, и теплообмен может осуществляться с двух сторон. Приведем примеры определения температуры термически тонкого тела.
Пример. Металлическая пластина толщиной 2 см разделяет два потока воздух с температурой  . Коэффициент теплоотдачи с горячей стороны
. Коэффициент теплоотдачи с горячей стороны  ; с холодной стороны
; с холодной стороны  . В начальный момент температура пластины 20
. В начальный момент температура пластины 20  Определить изменение температуры со временем и изменение тепловых потоков в обе стороны, для пластины
Определить изменение температуры со временем и изменение тепловых потоков в обе стороны, для пластины  .
.
Уравнение баланса энтальпии пластины: 
Очевидно, что температура пластины будет удовлетворять условию
 , поэтому второй член в правой части вычитается, так как на этой стороне происходит охлаждение. Предположим, что пластина термически тонкая и тогда
, поэтому второй член в правой части вычитается, так как на этой стороне происходит охлаждение. Предположим, что пластина термически тонкая и тогда 
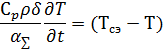
где  ,
,  – эквивалентная температура среды.
– эквивалентная температура среды.
Проверка дает Bi=  . Это означает, что пластина является термически тонким телом. Далее используется решение (34)
. Это означает, что пластина является термически тонким телом. Далее используется решение (34)

|
 , при t
, при t  температура пластины стремится к величине
температура пластины стремится к величине

Тепловой поток из среды 1 в пластину: 
Вычислим следующие величины:


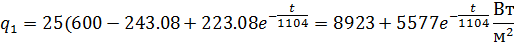
Тепловой поток, уходящий в холодную сторону:


При t  тепловые потоки выравниваются, причем тепловой поток с горячей стороны всегда больше, и пластина нагревается.
тепловые потоки выравниваются, причем тепловой поток с горячей стороны всегда больше, и пластина нагревается.
Пример. Определить изменение температуры поверхности стального листа толщиной 5 мм, если температура среды меняется по закону
 Определить минимальный расход воды, необходимый для орошения поверхности, чтобы температура не превышала 600
Определить минимальный расход воды, необходимый для орошения поверхности, чтобы температура не превышала 600  .
.
Величина 
 Коэффициент теплоотдачи 20
Коэффициент теплоотдачи 20 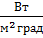
Минимальный расход воды будет соответствовать моменту, когда температура листа будет максимально допустимой 600  . Этот расход должен компенсировать поток идущий внутрь листа в этот момент.
. Этот расход должен компенсировать поток идущий внутрь листа в этот момент.
Уравнение теплового баланса для листа:
 или
или 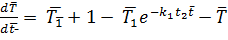
Используя (35) получается: 
Здесь 1,99= 

Учитывая, что при t ̅=0  получаем для С1= - 60,1.
получаем для С1= - 60,1.
В результате получаем решение 
Из последнего выражения необходимо найти время, когда Т=600  или
или
 , то есть решить уравнение -11+60,1
, то есть решить уравнение -11+60,1  .
.
Примем, что  .
.
Если теперь положить  .
.
В результате получается решение  и
и 
В этот момент тепловой поток, идущий внутрь листа равен:

Минимальный расход воды(распыленной) определяется из условия:
 (
( )=4270 Вт/м2
)=4270 Вт/м2
 =
= 


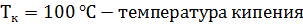
Если учесть, что пар нагревается выше температуры кипения до  , то в знаменателе еще появится слагаемое:
, то в знаменателе еще появится слагаемое:

В этом случае  =1,36
=1,36 
3.4. Случай плоской пластины 
В общем случае для плоской пластины толщиной  , когда она и не термически толстая и не термически тонкое, при граничных условиях:
, когда она и не термически толстая и не термически тонкое, при граничных условиях:


и начальных условиях  решение имеет вид бесконечного ряда []
решение имеет вид бесконечного ряда []
 (36)
(36)
 (37)
(37)
где  корни характеристического уравнения:
корни характеристического уравнения:
 (38)
(38)
Особенность корней последнего уравнения состоит в том, что эти корни возрастают с увеличением номера. При малых значениях  первый корень
первый корень  , а при
, а при 
 . Далее корни растут примерно на
. Далее корни растут примерно на  . Так при малых
. Так при малых 
 и при больших
и при больших 
 . Если учесть, что зависимость решения (36) от времени определяется множителем
. Если учесть, что зависимость решения (36) от времени определяется множителем  , то с увеличением номера этот множитель значительно уменьшается. При консервативной оценке:
, то с увеличением номера этот множитель значительно уменьшается. При консервативной оценке:  и
и 
 Кроме того, уменьшается с ростом номера величина
Кроме того, уменьшается с ростом номера величина  , которая к тому же является знакопеременной. В результате отмеченных свойств величин
, которая к тому же является знакопеременной. В результате отмеченных свойств величин  и
и  ряд (36) быстро сходится и при
ряд (36) быстро сходится и при 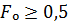 учет только одного первого члена ряда обеспечивает точность для температуры поверхности 0,5% [1]. При предыдущем рассмотрении термически толстых тел было установлено, что для времен соответствующих
учет только одного первого члена ряда обеспечивает точность для температуры поверхности 0,5% [1]. При предыдущем рассмотрении термически толстых тел было установлено, что для времен соответствующих  при определении температуры поверхности, а следовательно, и потока тепла внутрь тела, справедливо использовать выражения для термически толстого тела, а для случая
при определении температуры поверхности, а следовательно, и потока тепла внутрь тела, справедливо использовать выражения для термически толстого тела, а для случая  достаточно использовать только один первый член ряда. Однако значения
достаточно использовать только один первый член ряда. Однако значения  и
и  зависят от
зависят от  , поэтому необходимо пользоваться таблицами значений
, поэтому необходимо пользоваться таблицами значений  ,
,  (
( ) и
) и 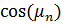 и
и  , что неудобно. Из (37) и (38) легко увидеть, что при изменении
, что неудобно. Из (37) и (38) легко увидеть, что при изменении  от 0 до
от 0 до 
 изменяется от
изменяется от  до
до  ,
,  от 1 до 1,2732. Таким образом, при малых
от 1 до 1,2732. Таким образом, при малых  и
и  тоже малый, поэтому для
тоже малый, поэтому для  , получим разложение (37) и (38)
, получим разложение (37) и (38)


Температура поверхности в этом случае выражается
 (39)
(39)
В случае, если падающий потом чисто конвективный, то

При малых 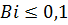 выражение (39) переходит в выражение для термически тонкого тела
выражение (39) переходит в выражение для термически тонкого тела  .
.
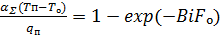 (40)
(40)
Нетрудно видеть, что  . Сравнение с решением (36) показывает, что при
. Сравнение с решением (36) показывает, что при  решение (39) дает хорошие результаты с точностью до 3%. Чтобы получить решение при больших значениях
решение (39) дает хорошие результаты с точностью до 3%. Чтобы получить решение при больших значениях 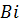 воспользуемся свойством
воспользуемся свойством  при
при  . Представим
. Представим  , где
, где 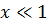 и тогда из (38) следует:
и тогда из (38) следует:

В результате приближенного решения последнего уравнения получается:
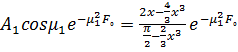 (41)
(41)
где
 ;
;  (42)
(42)
При заданном  по (42) определяем
по (42) определяем  и
и  , а затем по (41)
, а затем по (41)  и, наконец, по первому члену ряда определяем температуру:
и, наконец, по первому члену ряда определяем температуру:
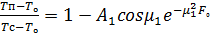 (43)
(43)
Выражения (41) и (42) можно использовать при  до
до  . При больших
. При больших  [3]
[3]
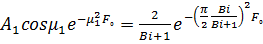 (44)
(44)
При вычислениях следует всегда иметь ввиду, что выражения (39), (41), (42), (43), (44) следует применять только при 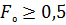 . Для более ранних стадий прогрева следует применять выражения для термически толстых тел. Выражения (41), (42), (43) тем точнее, чем больше
. Для более ранних стадий прогрева следует применять выражения для термически толстых тел. Выражения (41), (42), (43) тем точнее, чем больше  .
.
Пример: Определить температуру поверхности бетонной плиты 


 . На одну поверхность падает тепловой поток
. На одну поверхность падает тепловой поток 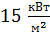 , другая поверхность теплоизолирована. Поверхность плиты охлаждается конвективным потоком воздуха, температура которого
, другая поверхность теплоизолирована. Поверхность плиты охлаждается конвективным потоком воздуха, температура которого  , коэффициент теплоотдачи конвекции
, коэффициент теплоотдачи конвекции  .
.
1. Критерий 
2. В течение времени 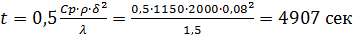 плита будет термически толстым телом.
плита будет термически толстым телом.
3. Характерное время изменения температуры поверхности плиты 
4. К моменту, когда 

5. До момента  и
и  температура поверхности определяется выражением (23):
температура поверхности определяется выражением (23):

6. При 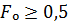 и при
и при  температура поверхности определяется выражением (39). Для времени соответствующем
температура поверхности определяется выражением (39). Для времени соответствующем  получается:
получается:


Этот результат абсолютно совпадает с результатом со стороны  .
.
7. По истечении 4х часов, когда  температура поверхности определяется как:
температура поверхности определяется как:


Пример: Определить температуру обогреваемой поверхности в условиях предыдущего примера для плиты толщиной  .
.
1. Критерий 
2. В течении времени  плита остается термически толстой.
плита остается термически толстой.
3. Характерное время прогрева поверхности плиты 
4. К моменту времени 

5. Для времени  как и в предыдущем примере
как и в предыдущем примере 
6. Для времени  , что соответствует
, что соответствует  температура поверхности определяется по соотношению (24) при
температура поверхности определяется по соотношению (24) при  снизу
снизу


7. При  и
и  температура поверхности определяется по выражениям (41)-(43). По (42) и (43) для
температура поверхности определяется по выражениям (41)-(43). По (42) и (43) для 



8. Температура поверхности к моменту времени соответствующему времени 



Что отличается от величины  снизу при
снизу при  на
на  .
.
9. В дальнейшем температура поверхности определяется для 

Пример: Определить изменение температуры поверхности плиты, описанной в предыдущих примерах с 
1. Число  .
.
2. В течение времени  плита остается термически толстым телом.
плита остается термически толстым телом.
3. Характерное время изменения температуры поверхности  как и прежде
как и прежде  сек.
сек.
Температура поверхности к моментам времен 
 для
для 

4. Температура плиты при  , что соответствует
, что соответствует  определяется по (24)
определяется по (24)


5. Температура плиты при том же времени  или сверху по предыдущему определению определяется для
или сверху по предыдущему определению определяется для  по соотношению (44)
по соотношению (44)

Для 


Расхождение значений температуры  определенные для
определенные для  и для
и для  различаются на
различаются на 