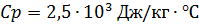
Поверхностное натяжение
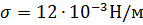
Коэффициент теплопроводности
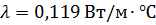
1. Определим давление насыщенного пара бутана при температуре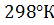 
, если при давлении 1 атм 
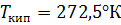, а теплота испарения 
.
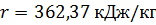Из уравнения Клазиуса-Клапейрона:
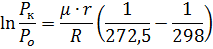
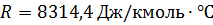
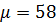
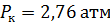
2. Коэффициент теплоотдачи при конвективном обтекании горячих газов:
;
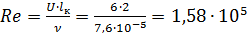lк – размер взаимодействия газов факела с поверхностью, S=4 м2.
Турбулентный режим
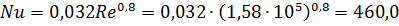
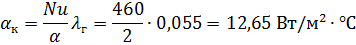
Коэффициент теплопроводности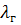 
взят при температуре 
.
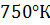3. В начальный момент теплообмен внутри резервуара будет осуществляться за счет естественной конвекции, которая развивается вследствие нагрева стенки
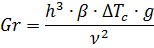
В данном случае перепад температур между стенкой и жидким бутаном не определен. Задача состоит в том, чтобы определить этот перепад для момента окончания режима свободной конвекции и перехода его в режим пузырькового кипения. Для этого приравниванием тепловой поток от стенки в режиме конвекции и пузырькового кипения
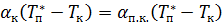
При условии турбулентной конвекции это равенство сводится к
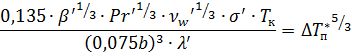
где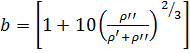 
При подстановке значений указанных величин получится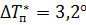 
, то есть при температуре стены 
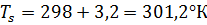начинается пузырьковое кипение. В этот момент тепловой поток от стенки в бутан равен:
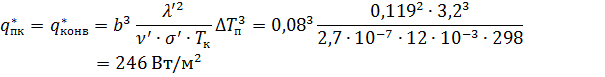
4. Дальнейший анализ величины тепловых потоков проводится по следующей схеме.
Определяем критический тепловой поток при пузырьковом кипении
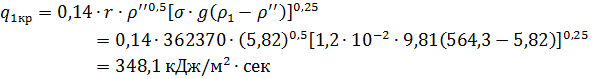
Из (61) и (64) определяем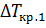 
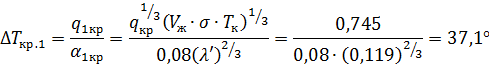
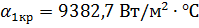
5. Тепловой баланс для стенки резервуара
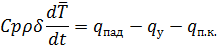
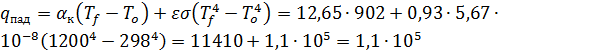вт/м2
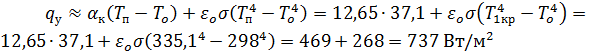
При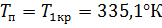 
6. Из сравнения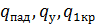 
можно сделать вывод, что величиной 
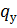можно пренебречь и в рассматриваемом случае стенка резервуара нагреется до уровня, когда 
.
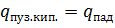7. Температура до которой нагреется стенка определяется из условия:
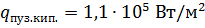
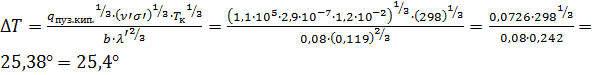
8. Коэффициент теплоотдачи в точке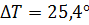 
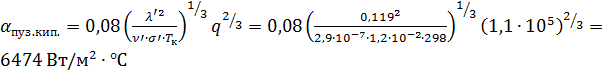
Максимальное значение 
Таким образом, ориентировочное значение максимальной температуры стенки резервуара достигает значение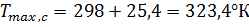 
.
Примечание: температура стенки будет быстро расти в случае, если падающий тепловой поток преодолеет значение q1 кр.
Пример: Рассмотреть предыдущий случай, если падающий тепловой поток превышает 
. Определить конечную равновесную температуру стенки, если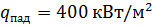 
. Такой высокий тепловой потом может быть в случае, если источник излучения имеет температуру 
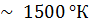и горячий излучающий газ обтекает резервуар с высокой скоростью, так что 
.
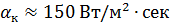1. Так как падающий тепловой поток превышает , то из-за кризиса кипения теплоотвод резко уменьшится, и новое равновесие установится при более высокой температуре во время пленочного кипения.
Тепловой баланс для стенки
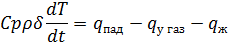
Потеря в газ и в жидкость за счет излучения составляет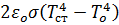 
. И множитель «2» учитывает излучение в обе стороны.
Поток уходящий за счет конвекции в газ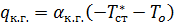 
, поток уходящий за счет пленочного кипения на испарение 
.
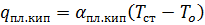2. При равновесии температура стенки постоянна и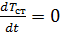 
. Поэтому
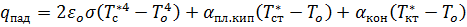
Коэффициент теплоотдачи при пленочном кипении бутана (53)
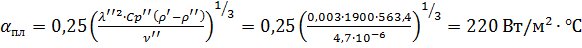
Физические величины для пара брались при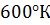 
.
Равновесная температура стенки определяется из условия равенства падающего потока и суммы уходящих по обе стороны стенки
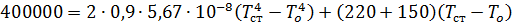
Применяем метод последовательных приближений
1. Пусть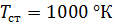 
тогда правая часть равна:
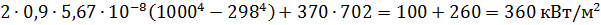
что меньше, чем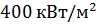 
падающего потока.
2. Пусть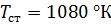 
, правая часть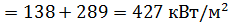 
3. 
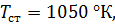правая часть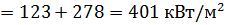 
что хорошо совпадает с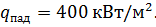 
Таким образом, температура стенки может подняться до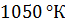 
, что немного хуже приведет к разрушению резервуара, так как при температуре стали выше 
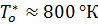прочность металла резко снижается.
Пример: В условиях предыдущего примера рассмотреть случай мгновенного разрушения резервуара и охлаждение жидкого бутана оставшегося в резервуаре до температуры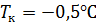 
. Температура стенки за время мгновенного испарения не изменялась и осталась равной 25 0С. Определить испарение бутана за счет теплообмена со стенкой резервуара. Толщина стенки резервуара 
.
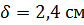1. Начальная разность температур (температурной напор)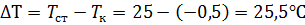 
меньше, чем 
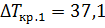(см. предыдущий пример), поэтому в начальный момент устанавливается пузырьковое кипение с начальным тепловым потоком:
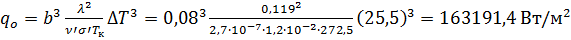
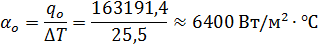
При этом 
и стенка не является термически тонким телом.
2. При пузырьковом кипении изменение теплового потока от стенки при охлаждении стенки не совпадает с тепловым потоком при ее нагревании при одном и том же тепловом напоре. Кипение бутана происходит за счет теплового ресурса стенки, и величина теплового потока при охлаждении больше, чем при нагревании стенки при одном и том же температурном напоре (явление гестерезиса). Величина теплового потока при пузырьковом кипении в режиме охлаждения стенки будет определяться из условия, что температурный напор уменьшается. При этом скорость роста пузыря уменьшится согласно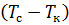 
, а плотность центров парообразования сохраняется на уровне начального или начального температурного напора[5]. Это значит, что тепловой поток будет определяться начальным коэффициентом теплоотдачи 
.
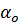В таком случае температура стенки будет в течении времени, соответствующего условию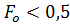 
как термически толстого тела 
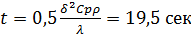. Так как 
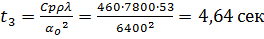, то 
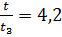и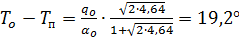 
, 
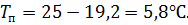
Тепловой поток к этому времени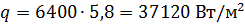 
.
3. За время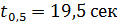 
или 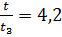из стенки уйдет количество тепла
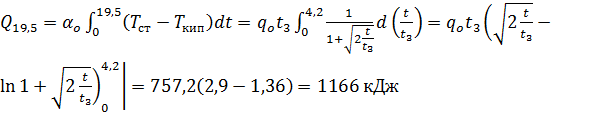
Полный тепловой ресурс стенки толщиной 24 мм при охлаждении от 25 до -0,5 
составляет
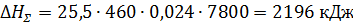
Таким образом, за первые 19,5 сек израсходуется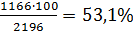 
ее теплового ресурса.
За это время с одного квадратного метра стенки выкипит
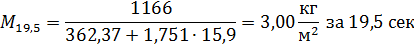
При вычислении учтено тепло уносимое паром со средней температурой
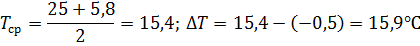
4. При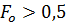 
теплообмен будет описываться выражением (44) справедливым для 
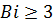. В рассматриваемом случае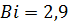 
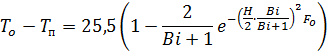
Для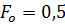 
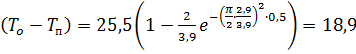
что неплохо согласуется с результатом для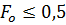 
снизу.
Тепловой поток из пластины на кипение
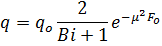
Количество тепла ушедшее из пластины с момента 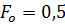до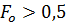
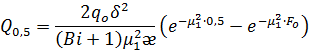
Для:
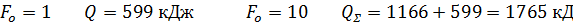
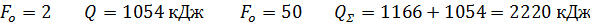
Приложение А.
Процессы молекулярного переноса, то есть диффузия, теплопроводность и вязкость, имеют в своей основе одно явление: перенос массы, перенос энергии и перенос импульса за счет движения молекул рассматриваемой среды. Для переноса соответствующего физического свойства среды необходимо, чтобы это свойство было неравномерно распределено в среде, то есть существует градиент в распределении этих свойств.