Соединение потребителей звездой и треугольником.
1. Фазные и линейные напряжения и токи. Трехфазные приемники электрической энергии (электрические двигатели) и группы однофазных приемников (электрические лампы, нагревательные приборы и т. д.), так же как и обмотки генератора, соединяют звездой или треугольником. Рассмотрим соединение звездой. Такое соединение применяется в том случае, когда каждая фаза приемника рассчитана на напряжение в √3 раз меньшее линейного напряжения сети. Осветительную нагрузку при этом разделяют на три приблизительно одинаковые по мощности группы — фазы приемника (рис. 50). Фазу 1 подключают к линейному проводу А и нейтральному N, фазу 2- к В и N, а фазу 3 - к С и N. На рис. 50 показана схема соединения звездой обмоток трехфазного электродвигателя. Концы обмоток соединены в общую (нейтральную) точку, а к началам обмоток А, В и С подключены соответствующие линейные провода. На рис. 51 показана схема четырехпроводной трехфазной цепи. В ней соединены звездой не только фазы приемника энергии, но и фазы питающего генератора (или
трансформатора). Начала фаз генератора А, В, С соединяются с началами фаз приемника А’, В’, С’ линейными проводами.
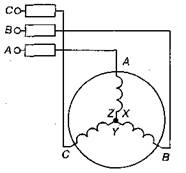
Рис. 50 Нейтральная точка
Нейтральная точка N генератора соединяется с нейтральной точкой N' приемника энергии нейтральным проводом. Ток, напряжение и мощность каждой фазы применка называются фазными. Ток первой фазы обозначают IА, второй — IB и третьей — IC. Положительное направление этих токов совпадает с положительным направлением ЭДС обмоток генератора. Токи в линейных проводах называются линейными. В рассматриваемой схеме одноименные фазы приемника, генератора и соответствующий линейный провод соединены последовательно. Поэтому токи IА, IB, IC являются также линейными и фазными токами генератора. Фазные напряжения приемника энергии обозначим, а фазные напряжения генератора соответственно UA, UB, UC.
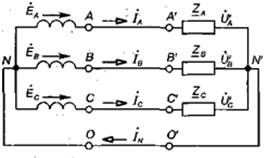
Рис. 51 Рис. 52
2. Расчет четырехпроводной трехфазной цепи. Сопротивления соединительных проводов зависят от протяженности линии электропередачи. В коротких линиях эта сопротивления незначительны и их можно не учитывать. При этом отсутствует падение напряжения в проводах, а фазные напряжения приемника равны соответствующим фазным напряжениям генератора: U'A=UA, U'B=UB, U'C=UC. Фазные токи приемника энергии определяются по закону Ома: İA= UA/ Z A, İB = UB/ Z B, İC= UC / Z C, где Z A=ZejφA, Z B=ZejφB, Z C=ZejφC.
Toк в нейтральном проводе по первому закону Кирхгофа равен сумме фазных токов:
İn = İA + İB + İC
При симметричной системе фазных напряжений и симметричной нагрузке, т. е при равенстве комплексов сопротивлений фаз приемника, токи İA, İB, İC, образуют симметричную трехфазную систему токов. В этом случае İA + İB + İC = 0 и ток в
нейтральном проводе отсутствует. При этих условиях отключение нейтрального провода не изменяет режима работы трехфазного приемника энергии. Поэтому к трехфазному электродвигателю (рис. 50) подключают только линейные провода. При несимметричных нагрузке или системе фазных напряжений в нейтральном Проводе имеется некоторый ток İn, который можно определить, применяя комплексные числа, или графически. Сущность графического метода поясним на примере.
Пример 15.1. Каждая фаза приемника энергии, соединенного звездой, состоит из
активного и. индуктивного сопротивлений.
Известны токи фаз и углы Сдвига фаз: IА = IВ = 5 А, IС = 7 А, φА = φВ = φС = 45°. Определить ток IN в нейтральном проводе графическим методом.
Решение. Для определения тока In построим векторную диаграмму напряжений
и токов (рис. 15.17). Сначала строим векторы фазных напряжений UA, UB, UС, сдвинутые друг относительно друга на 120°. Далее, задаваясь масштабом, строим вектор первого фазного тока 1А.
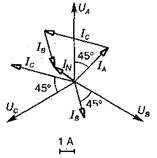
Рис.53
При активно-индуктивной нагрузке вектор IА повернут относительно вектора UA на 45° по ходу часовой стрелки. Аналогично строим векторы IВ и IС. Геометрически сложив векторы IА IВ и IС, найдем IN = 2А. '
3. Мощность трехфазной цепи. Мощность трехфазной цепи равна сумме мощностей отдельных, фаз, т. е. Р= РА + РB + РC. Активная мощность первой фазы приемника РА=UA·IA·cos φA,, где: UA и IA —напряжение и ток первой фазы приемника; φA, — угол сдвига между напряжением UA и током IA. Активная мощность второй фазы приемника РB=UB·IB·cos φB, а третьей РC=UC·IC·cos φC. При симметричной нагрузке активные мощности фаз приемника РА= РB= РC = Рф = Uф·Iф·cos φф. При этом условии активная мощность трехфазной цепи
Р= 3Рф=3·Uф·Iф·cosφ=3·(Uл/√3)·Iл·cosφ=√3·Uл·Iл·cos φ.
При соединении приемников энергии звездой Uф = Uл/√3 и Iф = Iл. Подставив эти значения в формулу активной мощности трехфазной цепи, получим
Р = 3·Uф·Iф·cosφ =3·(Uл/√3)·Iл·cosφ =√3·Uл·Iл·cos φ. (15.5)
Пример 15.2. По данным предыдущего примера определить активную
мощность трехфазной цепи, если фазное напряжение приемника
Uф=UA= UB = UC = 220 В.
Решение. Активные мощности фаз приемника: РA = UA·IA·cosφА =220·5·cos45°= 777 Вт; PB=UB·IB·cosφА =220·5·cos45°= 777 Вт; РC = UC·IC·cosφC =220·7·cos45°=1089Вт. Активная мощность трехфазной цепи Р= РA + РB+ РC = 777 + 777 + 1089 = 2643 Вт.