Роль нейтрального провода при соединении приемников энергий звездой

1. Обрыв фазы приемника при отключенном нейтральном проводе. Ранее были рассмотрены свойства трехфазной системы при соединении приемников энергии звездой. При симметричной нагрузке, когда Z _A = Z _B = Z _C, отключение, нейтрального провода не меняет режима работы электрической цепи. Векторная диаграмма для этого случая показана на рис. 54.

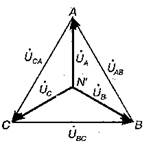
Рис. 54

Векторы линейных напряжений U_AB, U_BC, U_CA образуют замкнутый треугольник, а векторы фазных напряжений приемника и генератора U_A, U_B, U_C расходятся к вершинам А, В, С из точки N', которая находится в центре треугольника. Такая диаграмма справедлива и для симметричной нагрузки, с нейтральным проводом. На рассмотренной диаграмме все фазы приемника энергии находятся под одинаковым: напряжением U_ф = U_л/√3. Рассмотрим один из несимметричных режимов работы трехфазной цепи при отключенном нейтральном проводе. Допустим, что произошел разрыв фазы A (Z _A = ∞) при одинаковых сопротивлениях фаз В и С (Z _B = Z _С) и симметричных напряжениях генератора (рис. 55).

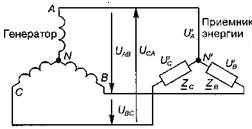
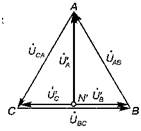
Рис.56 Рис.57

При этом цепь, с последовательным соединением двух равных сопротивлений Z _B и Z _С будет находиться под линейным напряжением U_BC. Падения напряжения на них будут одинаковы и равны половине напряжения U_BC. Следовательно, нейтральная точка N' окажется посередине отрезка ВС (рис.15.20). Соединив точку N' _: с вершинами треугольника А, В и С, получим векторы фазных напряжений Ů'_А, Ů'_B, Ů'_C.

Пример 15.3. Определить напряжение на первой фазе приемника
(см. рис. 15.20) при отключенном нейтральном проводе, если Z _A =∞ (обрыв первой фазы), a Z _B = Z _C.

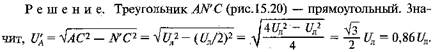
Короткое замыкание фазы приемника при отключенном нейтральном проводе. Рассмотрим несимметричную нагрузку, когда Z _A = 0 (короткое замыкание первой фазы приемника), Z _B = Z _C (рис. 58). При этом варианте линейный провод A непосредственно соединяется с нейтральной точкой приемника энергии. Поэтому напряжение на первой фазе приемника уменьшается до нуля, а на второй и третьей - увеличивается до линейного напряжения: U'_A = 0;U'_B= U_AB; U'_C =U_CA. При этом нейтральная точка N' совпадает с вершиной А треугольника (рис. 59). При переходе от первою варианта несимметричной нагрузки ко второму, т. е. при уменьшении сопротивления Z _A от ∞ до 0 и Z _B = Z _C, нейтральная точка будет перемещаться вверх по прямой линии (см. рис. 15.20) в точку А. При этом напряжение на первой фазе приемника будет уменьшаться от 0,86· U_л, до 0, а второй и третьей — увеличиваться от U_л /2 до U_л.

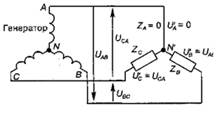
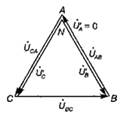
Рис. 58 Рис. 59

Из приведенного можно сделать следующий вывод: при несимметричной нагрузке и отключенном нейтральном проводе происходит смещение точки N' приемника из центра треугольника линейных напряжений генератора, в результате этого изменяются фазные, напряжения приемника электрической энергии. Более загруженные фазы приёмника (с меньшим полным сопротивлением) оказываются под меньшим фазным напряжением, а менее загруженные (с большим полным сопротивлением) – под большим.

Определение фазных напряжений приемника. Для определения фазных напряжений приемника используется метод комплексных чисел. Сначала определяют напряжение между точками N' и N (см. рис. 15.16), называемое напряжением смещения нейтрали. Его комплексное значение определяют по методу узлового напряжения:

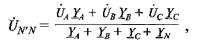
где Ů_А, Ů_B, Ů_C — комплексы фазных напряжении генератора; Y _А, Y _B, Y _C
комплексные проводимости фаз приемника; комплексная проводимость нейтрального провода. При отключенном нейтральном проводе Y _N =0, Комплексы фазных напряжений приемника:

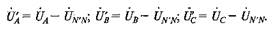
На рис. 60 показана топографическая диаграмма трехфазной цепи при несимметричной нагрузке, соединенной звездой. Обозначенным здесь точкам А, В,, N, N' соответствуют одноименные точки электрической цепи (рис. 51). При наличии нейтрального провода, сопротивлением которого можно пренебречь (Y _N = ∞), напряжение смешения нейтрали Ů_N'N = 0. В этом случае точка N' на топографической диаграмме сместится в точку N. В результате фазные напряжения приемника энергии будут одинаковыми. Таким образом, нейтральный провод обеспечивает выравнивание напряжений на фазах потребителя при несимметричной нагрузке. Четырехпроводные трехфазные системы широко применяются для осветительной нагрузки.

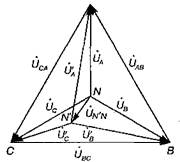
Рис. 60

При этом номинальное напряжение ламп равно фазному напряжению
сети. Во избежание разрыва цепи нейтрального провода в нем не устанавливают предохранителей и выключателей.

Пример 15.4. В схеме соединения трехфазного генератора и приемника звездой отключен нейтральный провод. Линейное напряжение генератора U_л = 220 В, cопротивления фаз приемника Z _A =(8 +j4) Ом; Z _B = (8 -j4) Ом; Z _С = 6 Ом. Сопротивление линейных проводов не учитывается. Определить фазные напряжения и токи приемника.

Решение. Комплексы фазных напряжении генератора: Ů_A = U_л /√3== 220/√3 = 127 В; Ů_B =127е^-j120°=(-63,5-j110)В; Ů_C =127е^+j120°= (-63,5 + j110)В. Проводимости фаз приемника в комплексной форме Y _A = l/ Z _A = 1/(8+J4) =(0,1-J 0,05) См; Y _B =1/ Z _B = 1/(8 + 4) = (0,1 + j0,05) См; Y _С = 1/ Z _C = 1/6 = 0,167 См;

Напряжение смещения нейтрали

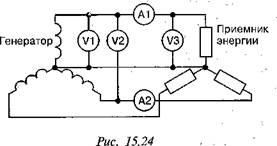
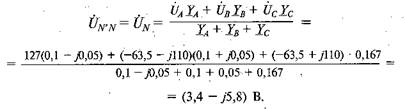
Напряжения на фазах приемника: Ů'_A= Ů_A - Ů_N =127 - 3,4 -j5,8= (123,6 + j5,8) В; Ů'_B = Ů_B - Ů_N = -63,5 - j110 - 3,4 + j5,8 = (-66,9 -j 104,2) В; Ů'_C = Ů_C - Ů_N = -63,5 + j110 - 3,4 + j5,8 =(-66,9-j115,8)В.
Фазные токи приемника: İ_А=Ů'_A· Y _A =(123,6+j5,8)(0,1–j0,05)=(12,7-j5,6) А; İ_В=Ů'_В· Y _В =

= (-66,9 –j104,2)(0,1 + j0,05) =(-1,5 -j13,7) А; İ_C=Ů'_C· Y _C = (-66,9 + j115,8)0,167 = (-11,2 – j19,3) А.

Правильность расчета определим по первому закону Кирхгофа:

İ_А + İ_В + İ_C = 12,7 -j5,6 - 1,5 j13,7 -11,2+ j19,3 = 0